《动手学深度学习》task3——过拟合、欠拟合及解决方案,梯度消失、梯度爆炸,循环神经网络进阶笔记
系统学习《动手学深度学习》点击这里:
《动手学深度学习》task1_1 线性回归
《动手学深度学习》task1_2 Softmax与分类模型
《动手学深度学习》task1_3 多层感知机
《动手学深度学习》task2_1 文本预处理
《动手学深度学习》task2_2 语言模型
《动手学深度学习》task2_3 循环神经网络基础
《动手学深度学习》task3_1 过拟合、欠拟合及其解决方案
《动手学深度学习》task3_2 梯度消失、梯度爆炸
《动手学深度学习》task3_3 循环神经网络进阶
《动手学深度学习》task4_1 机器翻译
《动手学深度学习》笔记:
《动手学深度学习》task1——线性回归、softmax与分类模型,多层感知机笔记
《动手学深度学习》task2——文本预处理,语言模型,循环神经网络基础笔记
《动手学深度学习》task3——过拟合、欠拟合及解决方案,梯度消失、梯度爆炸,循环神经网络进阶笔记
本篇目录
- 1 过拟合、欠拟合及其解决方案
- 1.1 python语法
- 1.2 为什么优化器中只对权重参数设置衰减,而不对偏置参数设置衰减呢?
- 1.3 过拟合、欠拟合的解决方案
- 1.4 如何设置丢弃率
- 1.5 reshape(m, n)和view(m, n)的区别
- 2 梯度消失、梯度爆炸
- 2.1 当神经网络的层数较多时,模型的数值稳定性容易变差。
- 2.2 随机初始化模型参数
- 2.3 PyTorch的默认随机初始化
- 2.4 Xavier随机初始化
- 2.5 环境因素
- 3 循环神经网络进阶
- 3.1 LSTM模型
1 过拟合、欠拟合及其解决方案
1.1 python语法
plt.semilogy()
'''对数坐标'''
plt.semilogx(x,y) # 对x取对数
plt.semilogy(x,y) # 对y取对数
plt.loglog(x,y) # 同时取对数
n = norm(v)返回向量v的欧几里德范数。此范数也称为 2-范数、向量模或欧几里德长度。
1.2 为什么优化器中只对权重参数设置衰减,而不对偏置参数设置衰减呢?
对偏置增加正则也是可以的,但是对偏置增加正则不会明显的产生很好的效果。而且偏置并不会像权重一样对数据非常敏感,所以不用担心偏置会学习到数据中的噪声。而且大的偏置也会使得我们的网络更加灵活,所以一般不对偏置做正则化。
1.3 过拟合、欠拟合的解决方案
欠拟合:模型无法达到较低的误差
解决:
- 模型的表现能力不够,换用更复杂的模型
- 模型的复杂度不够,增加模型的复杂度
过拟合:训练误差较低但是范化误差依然较高,二者相差较大
解决:
- 训练样本过少,增加样本
- 权重衰减(L2正则化)
- 丢弃法(dropout)
1.4 如何设置丢弃率
在多层感知机中,通常的建议是把靠近输入层的丢弃概率设得小一点
1.5 reshape(m, n)和view(m, n)的区别
.reshape(m,n)和.view(m,n)实质上是将元素重组为新的shape。
.reshape(m,n)只可用于numpy的ndarray,不可用于torch的tensor。
.view(m,n)对于numpy的ndarray和torch的tensor都可用
(即:对于tensor只能用.view(m,n))。
2 梯度消失、梯度爆炸
2.1 当神经网络的层数较多时,模型的数值稳定性容易变差。
假设一个层数为 L L L的多层感知机的第 l l l层 H ( l ) \boldsymbol{H}^{(l)} H(l)的权重参数为 W ( l ) \boldsymbol{W}^{(l)} W(l),输出层 H ( L ) \boldsymbol{H}^{(L)} H(L)的权重参数为 W ( L ) \boldsymbol{W}^{(L)} W(L)。为了便于讨论,不考虑偏差参数,且设所有隐藏层的激活函数为恒等映射(identity mapping) ϕ ( x ) = x \phi(x) = x ϕ(x)=x。给定输入 X \boldsymbol{X} X,多层感知机的第 l l l层的输出 H ( l ) = X W ( 1 ) W ( 2 ) … W ( l ) \boldsymbol{H}^{(l)} = \boldsymbol{X} \boldsymbol{W}^{(1)} \boldsymbol{W}^{(2)} \ldots \boldsymbol{W}^{(l)} H(l)=XW(1)W(2)…W(l)。此时,如果层数 l l l较大, H ( l ) \boldsymbol{H}^{(l)} H(l)的计算可能会出现衰减或爆炸。举个例子,假设输入和所有层的权重参数都是标量,如权重参数为0.2和5,多层感知机的第30层输出为输入 X \boldsymbol{X} X分别与 0. 2 30 ≈ 1 × 1 0 − 21 0.2^{30} \approx 1 \times 10^{-21} 0.230≈1×10−21(消失)和 5 30 ≈ 9 × 1 0 20 5^{30} \approx 9 \times 10^{20} 530≈9×1020(爆炸)的乘积。当层数较多时,梯度的计算也容易出现消失或爆炸。
2.2 随机初始化模型参数
在神经网络中,通常需要随机初始化模型参数。下面我们来解释这样做的原因。
回顾多层感知机一节描述的多层感知机。为了方便解释,假设输出层只保留一个输出单元 o 1 o_1 o1(删去 o 2 o_2 o2和 o 3 o_3 o3以及指向它们的箭头),且隐藏层使用相同的激活函数。如果将每个隐藏单元的参数都初始化为相等的值,那么在正向传播时每个隐藏单元将根据相同的输入计算出相同的值,并传递至输出层。在反向传播中,每个隐藏单元的参数梯度值相等。因此,这些参数在使用基于梯度的优化算法迭代后值依然相等。之后的迭代也是如此。在这种情况下,无论隐藏单元有多少,隐藏层本质上只有1个隐藏单元在发挥作用。因此,正如在前面的实验中所做的那样,我们通常将神经网络的模型参数,特别是权重参数,进行随机初始化。
2.3 PyTorch的默认随机初始化
随机初始化模型参数的方法有很多。在线性回归的简洁实现中,我们使用torch.nn.init.normal_()使模型net的权重参数采用正态分布的随机初始化方式。不过,PyTorch中nn.Module的模块参数都采取了较为合理的初始化策略(不同类型的layer具体采样的哪一种初始化方法的可参考源代码),因此一般不用我们考虑。
2.4 Xavier随机初始化
还有一种比较常用的随机初始化方法叫作Xavier随机初始化。
假设某全连接层的输入个数为 a a a,输出个数为 b b b,Xavier随机初始化将使该层中权重参数的每个元素都随机采样于均匀分布
U ( − 6 a + b , 6 a + b ) . U\left(-\sqrt{\frac{6}{a+b}}, \sqrt{\frac{6}{a+b}}\right). U(−a+b6,a+b6).
它的设计主要考虑到,模型参数初始化后,每层输出的方差不该受该层输入个数影响,且每层梯度的方差也不该受该层输出个数影响。
2.5 环境因素
-
协变量偏移:
输入分布 P(x)改变,条件分布 P(y∣x)不改变
如猫和狗中,训练数据使用的是猫和狗的真实的照片,但是在测试时,我们被要求对猫和狗的卡通图片进行分类。这就是输入特征发生了变化
-
标签偏移:
标签P(y)上的边缘分布的变化,但类条件分布P(x∣y)是不变的
如训练数据集,数据很少只包含流感p(y)的样本。 而测试数据集有流感p(y)和流感q(y),其中不变的是流感症状p(x|y)。
-
概念偏移:
条件分布 P(y∣x)发生了变化
如在建立一个机器翻译系统中,分布P(y∣x)可能因我们的位置的不同而发生变化
3 循环神经网络进阶
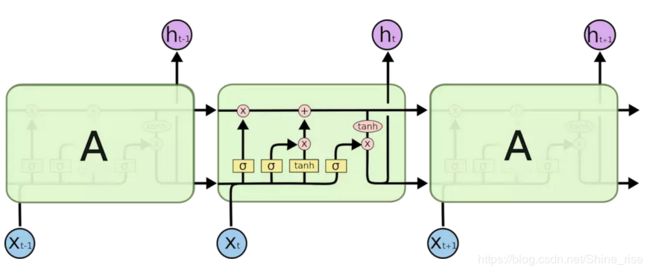
3.1 LSTM模型
-
遗忘门:
f t = σ ( W f ⋅ [ h t − 1 , x t ] + b f ) f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) ft=σ(Wf⋅[ht−1,xt]+bf)
该门会读取 h t − 1 h_{t−1} ht−1和 x t x_t xt,输出一个在 0 到 1 之间的数值给每个在细胞状态 C t − 1 C_{t-1} Ct−1中的数字。1 表示“完全保留”,0 表示“完全舍弃”。
-
输入门:
-
更新(输入门层):
i t = σ ( W i ⋅ [ h t − 1 , x t ] + b i ) i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right) it=σ(Wi⋅[ht−1,xt]+bi)
-
候选:
C ~ t = tanh ( W C ⋅ [ h t − 1 , x t ] + b C ) \tilde{C}_{t}=\tanh \left(W_{C} \cdot\left[h_{t-1}, x_{t}\right]+b_{C}\right) C~t=tanh(WC⋅[ht−1,xt]+bC)
sigmoid函数选择更新内容,tanh函数创建更新候选
我们把旧状态与$ f_t 相乘,丢弃掉我们确定需要丢弃的信息。接着加上相乘,丢弃掉我们确定需要丢弃的信息。接着加上 i_t * \tilde{C}_t$。这就是新的候选值,根据我们决定更新每个状态的程度进行变化。
C t = f t ∗ C t − 1 + i t ∗ C ~ t C_{t}=f_{t} * C_{t-1}+i_{t} * \tilde{C}_{t} Ct=ft∗Ct−1+it∗C~t
-
-
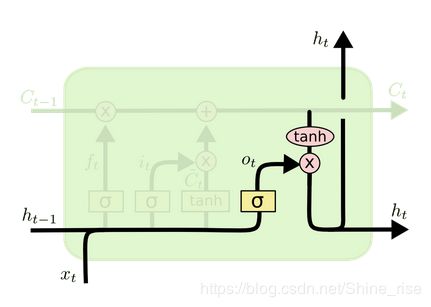
输出门:
o t = σ ( W o [ h t − 1 , x t ] + b o ) o_{t}=\sigma\left(W_{o}\left[h_{t-1}, x_{t}\right]+b_{o}\right) ot=σ(Wo[ht−1,xt]+bo)
h t = o t ∗ tanh ( C t ) h_{t}=o_{t} * \tanh \left(C_{t}\right) ht=ot∗tanh(Ct)
这三个门虽然功能上不同,但在执行任务的操作上是相同的。他们都是使用sigmoid函数作为选择工具,tanh函数作为变换工具,这两个函数结合起来实现三个门的功能。
遗忘门控制上一时间步的记忆细胞 C t − 1 \boldsymbol{C}_{t-1} Ct−1中的信息是否传递到当前时间步,而输入门则控制当前时间步的输入 X t \boldsymbol{X}_t Xt通过候选记忆细胞 C ~ t \tilde{\boldsymbol{C}}_t C~t如何流入当前时间步的记忆细胞。如果遗忘门一直近似1且输入门一直近似0,过去的记忆细胞将一直通过时间保存并传递至当前时间步。这个设计可以应对循环神经网络中的梯度衰减问题,并更好地捕捉时间序列中时间步距离较大的依赖关系。