《动手学深度学习》task4——机器翻译及相关技术;注意力机制与Seq2seq模型;Transformer笔记
系统学习《动手学深度学习》点击下面这个链接,有全目录哦~
https://blog.csdn.net/Shine_rise/article/details/104754764
本篇目录
- 1 机器翻译
- 1.1 数据预处理
- 1.2 Seq2Seq模型的构建
- 1.3 损失函数
- 1.4 训练
- 1.5 测试
- 2 注意力机制和Seq2seq模型
- 2.1 Softmax屏蔽
- 2.2 理解tensor中的二维,三维,四维
- 2.3 点积注意力(The dot product)
- 2.4 广播
- 2.5 多层感知机注意力
- 2.6 python中 `*args` 和 `**kwargs` 的使用
- 2.7 PyTorch 中 permute 的用法,与transpose,view比较
- 3 transformer
- 3.1 np.tile 和 np.repeat
- 3.2 BN和LN
1 机器翻译
1.1 数据预处理
- 读取数据,处理数据中的编码问题,并将无效的字符串删除
- 分词,分词的目的就是将字符串转换成单词组成的列表。目前有很多现成的分词工具可以直接使用,也可以直接按照空格进行分词(不推荐,因为分词不是很准确)
- 建立词典,将单词组成的列表编程单词id组成的列表,这里会得到如下几样东西 :
- 去重后词典,及其中单词对应的索引列表
- 还可以得到给定索引找到其对应的单词的列表,以及给定单词得到对应索引的字典。
- 原始语料所有词对应的词典索引的列表
- 对数据进行padding操作。因为机器翻译模型本质上是一个固定输入长度的Seq2Sqe模型,所以我们需要设置最大的数据长度,如果超出了设定的长度直接把后面的截断,少了的,根据需要进行不同的padding 添加
- 制作数据生成器,但是需要注意的是对于翻译任务的数据格式,机器翻译的输入是一段文本序列,输出也是一段文本序列。
1.2 Seq2Seq模型的构建
-
词嵌入,一般情况下输入到编码网络中的数据不是一个one-hot向量而是经过了编码之后的向量,比如由word2vec技术,让编码后的向量由更加丰富的含义。
-
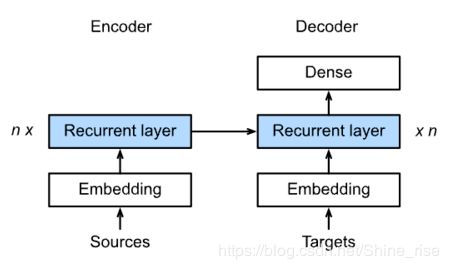
Seq2Seq模型有很多种,但是整体框架都是基于先编码后解码的框架。也就是先对输入序列使用循环神经网络对他进行编码,编码成一个向量之后,再将编码得到的向量作为一个新的解码循环神经网络的隐藏状态的输入,进行解码,一次输出一个序列的元素,再将模型训练输出的序列元素与真实标签计算损失进行学习。
-
在进行编码和解码的过程中数据都是以时间步展开,也就是(Seq_len,)这种形式的数据进行处理的
-
对于编码与解码的循环神经网络,可以通过控制隐藏层的层数及每一层隐藏层神经元的数量来控制模型的复杂度
-
编码部分,RNN的用0初始化隐含状态,最后的输出主要是隐藏状态,编码RNN输出的隐含状态认为是其对应的编码向量
-
解码器的整体形状与编码器是一样的,只不过解码器的模型的隐藏状态是由编码器的输出的隐藏状态初始化的。
-
解码器在rnn层之后还加了一层dense层,目的是将每一个隐藏单元的输出,映射到字典中,得到字典中每个单词出现的得分,然后选择出现得分最大的单词作为最终预测出的单词
-
编码器中主要用到的是state,它是语义编码的部分
解码器中主要用到的是out,用out生成每个时间步的单词
1.3 损失函数
在之前为了保证每个单词的向量长度一样,对单词进行了padding,那么在计算损失函数时,只需要计算原来单词的有效长度,需要把无效的单词padding部分去掉:
def SequenceMask(X, X_len,value=0):
maxlen = X.size(1)
mask = torch.arange(maxlen)[None, :].to(X_len.device) < X_len[:, None]
X[~mask]=value
return X
X = torch.tensor([[1,2,3], [4,5,6]])
SequenceMask(X,torch.tensor([1,2]))
输出:
tensor([[1, 0, 0],
[4, 5, 0]])
X = torch.ones((2,3, 4))
SequenceMask(X, torch.tensor([1,2]),value=-1)
输出:
tensor([[[ 1., 1., 1., 1.],
[-1., -1., -1., -1.],
[-1., -1., -1., -1.]],
[[ 1., 1., 1., 1.],
[ 1., 1., 1., 1.],
[-1., -1., -1., -1.]]])
mask的使用:
maxLen = 10
seq_len = 2
X_len = torch.LongTensor([3,4])
X = torch.rand((seq_len,maxLen))
y = torch.arange(maxLen)
print("y", y)
print("y[None,:]",y[None,:])
print('X_len', X_len)
print("X_len[:,None]", X_len[:,None])
mask = y[None,:] < X_len[:,None]
print('mask', mask)
print("~mask", ~mask)
X[~mask] = 0
print("X", X)
'''
y tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y[None,:] tensor([[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]])
X_len tensor([3, 4])
X_len[:,None] tensor([[3],
[4]])
mask tensor([[ True, True, True, False, False, False, False, False, False, False],
[ True, True, True, True, False, False, False, False, False, False]])
~mask tensor([[False, False, False, True, True, True, True, True, True, True],
[False, False, False, False, True, True, True, True, True, True]])
X tensor([[-1.1690, -0.4667, -0.9182, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000],
[ 0.1243, 0.5251, -0.7574, -0.6291, 0.0000, 0.0000, 0.0000, 0.0000,
0.0000, 0.0000]])
可见,None的作用是在None所处的维度上多一维,如
若原来tensor是一维的,为 tensor([1, 2, 3]),则 tensor 的 size 为 torch.Size([3])
[None, :]是在第一维上增加一维,变成tensor([[1, 2, 3]]), size 变为torch.Size([1, 3])[:, None]是在第二维上增加一维,变成tensor([[1], [2], [3]]), size 变为torch.Size([3, 1])
与此类似,若原来的tensor是二维的,使用了None之后就变成了三维,如[:, :, None]就是在第三维上增加一维
详细mask使用见链接
1.4 训练
在训练模型时,经过decoder的最后单词的形式为
# y的输出为如下形式: words
Y_input, Y_label, Y_vlen = Y[:, :-1], Y[:, 1:], Y_vlen - 1
Y_input:解码器输入的是法语words Y_label:解码器输出的是wordsY_vlen:有效长度减一(原有效长度仅包含 和其中的一个)
1.5 测试
-
解码器在测试的时候需要将模型的输出作为下一个时间步的输入
-
Beam Search搜索算法。
假设预测的时候词典的大小为3,内容为a,b,c. beam size为2,解码的时候过程如下 :
生成第一个词的时候,选择概率最大的两个词,假设为a,c.那么当前的两个序列就是a和c。
生成第二个词的时候,将当前序列a和c,分别与此表中的所有词进行组合,得到新的6个序列aa ab ac ca cb 计算每个序列的得分,并选择得分最高的2个序列,作为新的当前序列,假如为aa cb
后面不断重复这个过程,直到遇到结束符或者达到最大长度为止,最终输出得分最高的2个序列。
2 注意力机制和Seq2seq模型
由于带有注意机制的seq2seq的编码器与不带注意力机制的Seq2SeqEncoder相同,所以在此处我们只关注解码器。我们添加了一个MLP注意层(MLPAttention),它的隐藏大小与解码器中的LSTM层相同。然后我们通过从编码器传递三个参数来初始化解码器的状态:
- the encoder outputs of all timesteps:encoder输出的各个状态,被用于attention layer的memory部分,有相同的key和values
- the hidden state of the encoder’s final timestep:编码器最后一个时间步的隐藏状态,被用于初始化decoder 的hidden state
- the encoder valid length: 编码器的有效长度,借此,注意层不会考虑编码器输出中的填充标记(Paddings)
- Attention model的输出当作成上下文信息context vector,并与解码器输入拼接起来一起送到解码器
在解码的每个时间步,我们使用解码器的最后一个RNN层的输出作为注意层的query。然后,将注意力模型的输出与输入嵌入向量连接起来,输入到RNN层。虽然RNN层隐藏状态也包含来自解码器的历史信息,但是attention model的输出显式地选择了enc_valid_len以内的编码器输出,这样attention机制就会尽可能排除其他不相关的信息。
参考链接:深度学习中的注意力机制https://www.cnblogs.com/Luv-GEM/p/10712256.html
2.1 Softmax屏蔽
在使用attention时候,不需要计算padding的部分,所以需要把padding部分的value设为无穷小
def SequenceMask(X, X_len,value=-1e6):
maxlen = X.size(1)
#print(X.size(),torch.arange((maxlen),dtype=torch.float)[None, :],'\n',X_len[:, None] )
mask = torch.arange((maxlen),dtype=torch.float)[None, :] >= X_len[:, None]
#print(mask)
X[mask]=value
return X
def masked_softmax(X, valid_length):
# X: 3-D tensor, valid_length: 1-D or 2-D tensor
softmax = nn.Softmax(dim=-1)
if valid_length is None:
return softmax(X)
else:
shape = X.shape
if valid_length.dim() == 1:
try:
valid_length = torch.FloatTensor(valid_length.numpy().repeat(shape[1], axis=0)) # [2,2,3,3]
except:
valid_length = torch.FloatTensor(valid_length.cpu().numpy().repeat(shape[1], axis=0)) # [2,2,3,3]
else:
valid_length = valid_length.reshape((-1,))
# fill masked elements with a large negative, whose exp is 0
X = SequenceMask(X.reshape((-1, shape[-1])), valid_length)
return softmax(X).reshape(shape)
print(masked_softmax(torch.rand((3,2,4),dtype=torch.float), torch.FloatTensor([2,3])))
"""
tensor([[[0.5787, 0.4213, 0.0000, 0.0000],
[0.3868, 0.6132, 0.0000, 0.0000]],
[[0.3235, 0.2543, 0.4222, 0.0000],
[0.3500, 0.4183, 0.2317, 0.0000]]])
解释:
mask的用法与上面1.4相同
X是一个三维的
tensor,X shape: (batch_size, seq_length, embedding_length),embedding_length为词向量长度
valid_length是除了padding部分的有效长度,是一个一维或者二维的tensor,如果是一维的,
valid_length shape: (1, batch_size)如
valid_length = torch.FloatTensor([2, 4, 4])表明batch_size = 3,每个batch的句子的有效长度都是一样的,所以对于每个batch需要扩展到seq_length个有效长度如果是二维的,
valid_length shape有两种情况,(seq_length, batch_size)或者(batch_size, seq_length),全都用valid_length = valid_length.reshape((-1,))转化为一行,然后mask操作
2.2 理解tensor中的二维,三维,四维
无论几维,都可以按照(Batch_size, Height, Width, Channel)来理解。
- 二维:只有(Height, Width),而且理解的是对于每一 [] 从后向前看。即第一个[0.1, 0.2, 0.3]是width维度的。
b = [[0.1, 0.2, 0.3], [0.4, 0.5, 0.6]]
b_array = np.array( b )
print(b_array)
print(b_array.shape)
print( b_array[1,2] )
### result
[[0.1 0.2 0.3]
[0.4 0.5 0.6]]
(2, 3)
0.6
- 三维:只有(Height, Width, Channel),而且理解的是对于每一 维从后向前看。即第一个[1, 2, 3, 3.5]是Channel维度的。
a = [ [[1, 2, 3, 3.5], [4, 5, 6, 6.5]],
[[7, 8, 9, 9.5], [10, 11, 12, 12.5]],
[[13, 14, 15, 15.5], [16, 17, 18, 18.5]]]
a_array = np.array( a )
print(a_array)
print( a_array.shape )
print( a_array[0, 1, 3] )
### result
[[[ 1. 2. 3. 3.5]
[ 4. 5. 6. 6.5]]
[[ 7. 8. 9. 9.5]
[10. 11. 12. 12.5]]
[[13. 14. 15. 15.5]
[16. 17. 18. 18.5]]]
(3, 2, 4)
6.5
- 四维:(Batch_size, Height, Width, Channel),而且理解的是对于每一 [] 从后向前看。即第一个[0.1, 0.2, 0.3]是Channel维度的。
c = [ [[[0.1, 0.2, 0.3], [0.4, 0.5, 0.6], [0.7, 0.8, 0.9], [1.0, 1.1, 1.2]],
[[0.11, 0.21, 0.31], [0.41, 0.51, 0.61], [0.71, 0.81, 0.91], [1.01, 1.11, 1.21]] ],
[[[0.12, 0.22, 0.32], [0.42, 0.52, 0.62], [0.72, 0.82, 0.92], [1.02, 1.12, 1.22]],
[[0.112, 0.212, 0.312], [0.412, 0.512, 0.612], [0.712, 0.812, 0.912], [1.012, 1.112, 1.212]]]
]
c_array = np.array( c )
print( c_array )
print( c_array.shape )
print( c_array[1, 0, 3, 1] )
## result
[[[[0.1 0.2 0.3 ]
[0.4 0.5 0.6 ]
[0.7 0.8 0.9 ]
[1. 1.1 1.2 ]]
[[0.11 0.21 0.31 ]
[0.41 0.51 0.61 ]
[0.71 0.81 0.91 ]
[1.01 1.11 1.21 ]]]
[[[0.12 0.22 0.32 ]
[0.42 0.52 0.62 ]
[0.72 0.82 0.92 ]
[1.02 1.12 1.22 ]]
[[0.112 0.212 0.312]
[0.412 0.512 0.612]
[0.712 0.812 0.912]
[1.012 1.112 1.212]]]]
(2, 2, 4, 3)
1.12
参考链接:https://blog.csdn.net/holmes_mx/article/details/82813865
2.3 点积注意力(The dot product)
2.4 广播
参考链接:https://blog.csdn.net/lanchunhui/article/details/50158975?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task
a. 当操作两个array时,numpy会逐个比较它们的shape(构成的元组tuple),只有在下述情况下,两arrays才算兼容:
- 相等
- 其中一个为1,(进而可进行拷贝拓展已至,shape匹配)
b. 注意和矩阵乘法的区别,当有一维数组参与运算时:
- 一维数组置于矩阵乘法的左部,被视为一个行向量;
- 一维数组置于矩阵乘法的右部,被视为一个列向量;
- (这样和一个一维数组作用无论在左还是在右)矩阵乘法运算结束得到的向量仍是一维数组。
2.5 多层感知机注意力
class MLPAttention(nn.Module):
def __init__(self, units, ipt_dim, dropout, **kwargs):
super(MLPAttention, self).__init__(**kwargs)
self.W_k = nn.Linear(ipt_dim, units, bias=False)
self.W_q = nn.Linear(ipt_dim, units, bias=False)
self.v = nn.Linear(units, 1, bias=False)
self.dropout = nn.Dropout(dropout)
def forward(self, query, key, value, valid_length):
query = self.W_q(query)
key = self.W_k(key)
print('query_size', query.size()) # query (batch_size, queries, units)
print('key_size', key.size()) # key (batch_size, kv_pairs, units)
print('query_size_unsqueeze', query.unsqueeze(2).size()) # (batch_size, queries, 1, units)
print('key_size_unsqueeze', key.unsqueeze(1).size()) # (batch_size, 1, kv_pairs, units)
features = query.unsqueeze(2) + key.unsqueeze(1) # features (batch_size, queries, kv_pairs, units)
print('features_size', features.size())
m = nn.Tanh()
scores = self.v(m(features)).squeeze(-1) # scores (batch_size, queries, kv_pairs)
print('scores_size', scores.size())
attention_weights = self.dropout(masked_softmax(scores, valid_length))
return torch.bmm(attention_weights, value)
out:
query_size torch.Size([2, 1, 8])
key_size torch.Size([2, 10, 8])
query_size_unsqueeze torch.Size([2, 1, 1, 8])
key_size_unsqueeze torch.Size([2, 1, 10, 8])
features_size torch.Size([2, 1, 10, 8])
scores_size torch.Size([2, 1, 10])
就使用到了上面的广播机制。
2.6 python中 *args 和 **kwargs 的使用
*args用来将参数打包成tuple给函数体调用**kwargs用来将参数打包成dict给函数体调用- 参数
arg、*args、**kwargs三个参数的位置必须是一定的。必须是(arg, *args, **kwargs)这个顺序,否则程序会报错。
2.7 PyTorch 中 permute 的用法,与transpose,view比较
-
permute
对任意高维矩阵进行转置,但没有
torch.permute()这个调用方式, 只能Tensor.permute()。t.rand(2,3,4,5).permute(3,2,0,1).shape # Out[669]: torch.Size([5, 4, 2, 3]) -
transpose
只能操作 2D 矩阵的转置。
torch.transpose()和Tensor.permute()两种调用方式都可。连续使用
transpose也可实现permute的效果。torch.transpose(Tensor, 1, 0)t.rand(2,3,4,5).transpose(3,0).transpose(2,1).transpose(3,2).shape # Out[672]: torch.Size([5, 4, 2, 3]) -
view
可以理解为把原先 tensor 中的数据按照行优先的顺序排成一个一维的数据(这里应该是因为要求地址是连续存储的),然后按照参数组合成其他维度的 tensor。比如说是不管你原先的数据是
[[[1,2,3],[4,5,6]]]还是[1,2,3,4,5,6],因为它们排成一维向量都是6个元素,所以只要 view 后面的参数一致,得到的结果都是一样的
3 transformer
3.1 np.tile 和 np.repeat
分别查看官方文档,直接看官方文档中的栗子:
>>> a = np.array([0, 1, 2])
>>> np.tile(a, 2)
array([0, 1, 2, 0, 1, 2])
>>> np.tile(a, (2, 2))
array([[0, 1, 2, 0, 1, 2],
[0, 1, 2, 0, 1, 2]])
>>> np.tile(a, (2, 1, 2))
array([[[0, 1, 2, 0, 1, 2]],
[[0, 1, 2, 0, 1, 2]]])
>>> b = np.array([[1, 2], [3, 4]])
>>> np.tile(b, 2)
array([[1, 2, 1, 2],
[3, 4, 3, 4]])
>>> np.tile(b, (2, 1))
array([[1, 2],
[3, 4],
[1, 2],
[3, 4]])
>>> c = np.array([1,2,3,4])
>>> np.tile(c,(4,1))
array([[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4],
[1, 2, 3, 4]])
tile(A, reps): A为数组,reps 可以为数字或者元组
tile 怎么执行的?可以比较前面 2.2节 理解tensor中的二维,三维,四维,对数组来说,数组的形状 shape 都是一个tutle,那对每一个 tutle 的每一个维度,都可以从后向前看,比如
np.tile(b, 2):在第一个维度上重复二次np.tile(b, (2, 1)):从后往前看,在第一个维度上重复一次之后,在第二个维度上重复两次
>>> np.repeat(3, 4)
array([3, 3, 3, 3])
>>> x = np.array([[1,2],[3,4]])
>>> np.repeat(x, 2)
array([1, 1, 2, 2, 3, 3, 4, 4])
>>> np.repeat(x, 3, axis=1)
array([[1, 1, 1, 2, 2, 2],
[3, 3, 3, 4, 4, 4]])
>>> np.repeat(x, [1, 2], axis=0)
array([[1, 2],
[3, 4],
[3, 4]])
repeat(a, repeats, axis=None):a 为数组,repeats 可以为 int 或者是 int 类型的数组
repeat 的重复维度主要看axis这个属性,
-
axis=None,官方解释为 By default, use the flattened input array, and return a flat output array.先将原数组平铺为维数为 1 的数组,然后重复每个数字,最后返回的是一个扁平的输出数组
-
axis=1,列变化,在列上重复 -
axis=0,行变化,在行上重复
同时,np.tile和np.repeat的区别还在于,若原数组是tensor:
- tile返回的是数组
- repeat返回的是tensor
下面这个例子可以很清楚的看出他们的区别:
a = torch.tensor([4, 5, 6])
print(np.tile(a, 2))
print(np.repeat(a, 2, axis=0))
# out:
[4 5 6 4 5 6]
tensor([4, 4, 5, 5, 6, 6])
print(type(np.tile(a, 2)))
print(type(np.repeat(a, 2, axis=0)))
# out:
<class 'numpy.ndarray'>
<class 'torch.Tensor'>
3.2 BN和LN
BN 参考链接:https://zhuanlan.zhihu.com/p/54171297
LN 参考链接:https://zhuanlan.zhihu.com/p/54530247
在图中 N 表示样本轴, C 表示通道轴, F 是每个通道的特征数量。BN如右侧所示,它是取不同样本的同一个通道的特征做归一化;LN则是如左侧所示,它取的是同一个样本的不同通道做归一化。