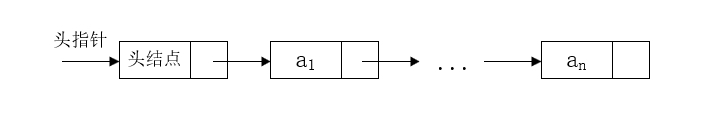数据结构与算法 —— 线性表之单链表

本文首发于我的个人博客：https://staunchkai.com

引言

上一篇的顺序存储结构中提到，顺序存储结构最大的缺点是 插入和删除时需要移动大量的元素， 这就需要耗费大量的时间。针对这个问题，线性表的链式存储就出现了。

「链式存储」 直接不考虑相邻位置的问题，哪里有位置就把元素放到哪里，每个元素多用一个位置来存放 指向下一个元素的指针，这样就可以从上一个元素找到下一个元素，它们之间的位置是随机的。

链式存储结构

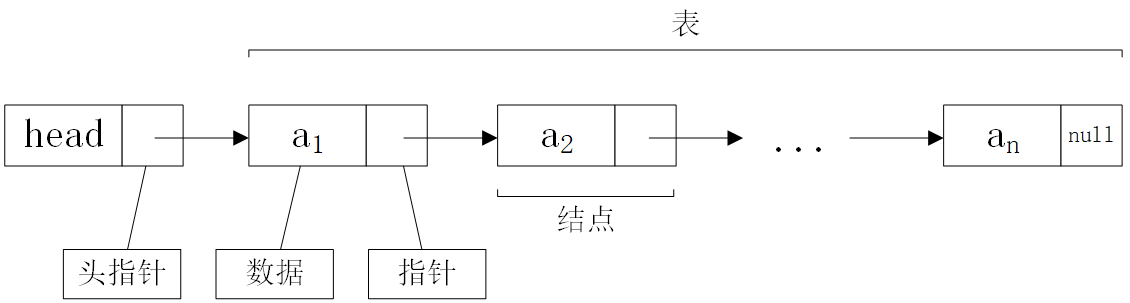
线性表链式存储结构是用一组任意的存储单元存放线性表的元素，这组存储单元可以存在内存中未被占用的任意位置。

相比与顺序存储结构，有如下区别：

• 顺序存储： 只需要存储一个位置（元素）
• 链式存储： 除了需要存储一个位置（元素），还需要存储它的后继元素的存储地址（指针）

我们把存储数据元素信息的域称为数据域（通俗的说，域就是地方），把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。这两部分信息组成的数据元素称为存储映像，称为结点（Node）。

链表的每个结点中只包含一个指针域，所以它叫做单链表。

对于线性表，都有一个头一个尾，在链式存储中，把链表的第一个结点的存储位置叫做头指针，最后一个结点指针为空（NULL），如上图所示。

链式存储 头结点 的数据域一般不存储任何信息，起着带头的作用即可，举个小旗子。

头指针 与 头结点 的区别：
头指针：

• 头指针是指向链表第一个结点的指针，若链表有头结点，则是指向头结点的指针
• 头指针具有标识的作用，常用头指针冠以链表的名字（指针变量的名字）
• 无论链表是否为空，头指针不为空
• 头指针是链表的必要元素

头结点：

• 头结点是为了操作的统一和方便而设定的，放在第一个元素结点之前，其数据域一般无意义（但是也可以用来存放链表的长度）
• 有了头结点，对在第一结点前插入结点和删除第一结点的操作，与其他后面的操作就统一了
• 头结点不一定是链表的必需要素

单链表存储结构

单链表如图所示：

空链表如图所示：

定义结构体

#include 
#include 

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

typedef int ElemType;
typedef int Status;
typedef struct Node
{
    ElemType data;  // 数据域
    struct Node *Next;  // 指针域（指向一个结点类型的指针）
} Node;
typedef struct Node *LinkList;

单链表的读取

在线性表的顺序存储结构中，要获取某个元素的存储位置是很容易的，但是在单链表中，获取某一个元素的位置，相对较为麻烦，因为我们不知道获取的元素位置到底在哪，必须从第一个结点开始一个一个的找下去。

获取链表第 i 个数据的算法思路：

1. 声明一个结点 p 指向第一个结点（因为必须从第一个结点开始寻找），初始化 j 从 1 开始；
2. 通过 j 来遍历链表，直到 j < i时（遍历到了 i 的时候就找到了），让 p 的指针不断向后移动，不断指向下一个结点， j + 1;
3. 若到链表末尾处，也就是 p 为空，则说明第 i 个元素不存在；
4. 若查找成功，返回结点 p 的数据。

/* 通过位置获取元素 */
Status GetElem(LinkList L, int i, ElemType *e)
{
    LinkList p; // 指针
    int j = 1;  // 用于遍历

    p = L->Next;    // p 指向链表的第一个结点

    while(p && j < i)    // p 不为空，p 为空指向的是链表尾部，当 j=i 已经找到了
    {
        p = p->Next;    // p 指向下一个结点
        j++;
    }

    if(!p)  // 当上一个循环 p 为 NULL，也就是 p 为假后退出，此处 !p 应该为真
        return ERROR;

    *e = p->data;

    return OK;
}

此算法的时间复杂度取决于 i 的位置，因此最坏情况下的时间复杂度为 O(n)。并且由于单链表结构中没有定义表长，不知道需要循环多少次，因此采用 while 循环比较合适。

单链表的插入

假设要存储的元素 e 的结点为 s，实现结点 p、p->next 和 s 之间的逻辑关系如下图：

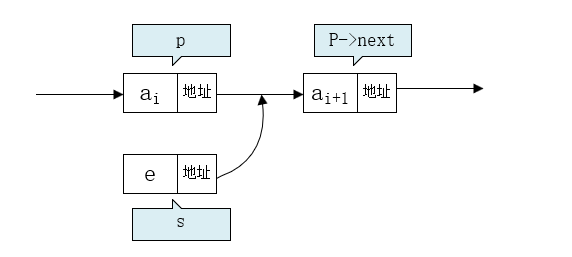
要将结点 s 插入进去，只需要将结点 p 指向 s，结点 s 指向结点 p->next。

单链表第 i 个数据插入结点的算法思路：

1. 声明一个结点 p 指向链表表头结点，初始化 j 从 0 开始；
2. 当 j < i 时，遍历链表，让 p 的指针向后移动，不断指向下一个结点，j + 1；
3. 若到链表末尾，此时 p 为空，说明第 i 个元素不存在；
4. 否则查找成功，生成一个空结点 s；
5. 将数据元素 e 赋值给 s->data；
6. 单链表插入，返回成功。

/* 插入元素 */
Status InsertElem(LinkList L, int i, ElemType e)
{
    LinkList p;
    int j = 0;
    p = L;

    while(p && j < i - 1)    // 用于寻找第 i 个结点
    {
        p = p->Next;
        j++;
    }

    if(!p)
        return ERROR;

    LinkList s;     //声明一个空结点
    s = (LinkList)malloc(sizeof(Node));     // 分配地址空间给 s
    s->data = e;    // 将要插入的元素赋值给 s 结点

    s->Next = p->Next;  // s 结点指向 p->next 结点
    p->Next = s;    // p 结点指向 s 结点

    return OK;
}

单链表的元素删除

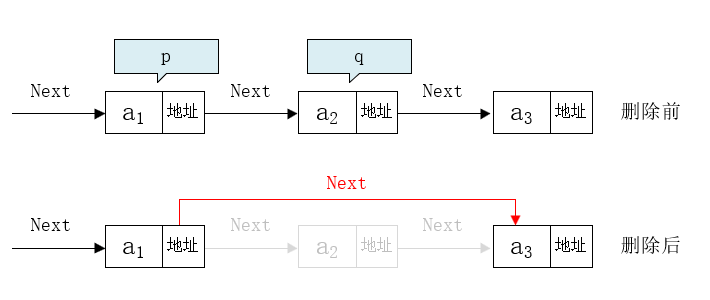
点链表删除第 i 个元素结点的算法思路：

1. 声明结点 p 指向链表第一个结点，初始化 j = 1；
2. 当 j < i 时，遍历链表，让 p 的指针向后移动，不断指向下一个结点，j + 1；
3. 若到链表末尾，此时 p 为空，说明第 i 个元素不存在；
4. 否则查找成功，将要删除的结点 p->next 赋值给 q；
5. 将原来的 q->next 赋值给 p->next；
6. 将 q 结点中的数据赋值给 e 作为返回；
7. 释放 q 结点。

/* 删除元素 */
Status DeleteElem(LinkList *L, int i, ElemType *e)
{
    LinkList p;
    int j = 1;

    p = *L;;

    while(p->Next && j < i)
    {
        p = p->Next;
        j++;
    }

    if(!(p->Next))
        return ERROR;

    LinkList q;
    q = (LinkList)malloc(sizeof(Node));
    q = p->Next;
    p->Next = q->Next;

    *e = q->data;
    free(q);

    return OK;
}

单链表的创建

单链表的数据不像顺序存储结构那么集中，它的数据分散在内存的各个角落，它的增长也是动态的。对于链表，所占用空间的大小和位置是不需要事先分配划定的，可根据情况和实际需求即使生成。

创建单链表的过程是一个动态生成链表的过程，从「空表」的初始状态起，依次建立各个元素的结点，并逐个插入链表。

单链表创建的算法思路如下：

1. 声明一个结点 p, 一个判断是否输入结束的变量 i；
2. 初始化一个空链表 L；
3. 让 L 的头结点的指针指向 NULL，即建立一个带头结点的单链表；
4. 循环实现后继结点的赋值和插入。

头插法（头部插入法）

头插法从一个空表开始，生成新结点，读取数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直至结束为止。简单来说，就是把新加入的元素放在表头后的第一个位置上：

1. 让新节点的 next 指向头结点之后的 NULL；
2. 然后让表头的 next 指向新结点。

始终让新结点插在第一的位置

例如：

// 要插入的元素有：
s t a u n c h k a i
// 使用头插法后为：
i a k h c n u a t s

/* 头插法建立单链表 */
void CreateListHead(LinkList *L)
{
    ElemType e;
    LinkList p;
    int i = 1;

    *L = (LinkList)malloc(sizeof(Node));    // 申请新结点内存空间
    (*L)->Next = NULL;  // 初始化
    printf("输入表中的数据元素，输入 -100 结束!\n");
    while(i)
    {
        scanf("%d", &e);
        if(e == -100)   // 当输入 -100 时，判断输入结束，结束循环
            i = 0;
        else
        {
            p = (LinkList)malloc(sizeof(Node)); // 申请新结点空间
            p->data = e;    // 将输入的数据存入到申请的结点空间域
            p->Next = (*L)->Next;   // 原来头结点的直接后继称为新结点的直接后继
            (*L)->Next = p; // 新结点变为头结点的直接后继
        }
    }
}

尾插法（尾部插入法）

上面的头插法生成链表后，输入的数据和结果的数据顺序相反，这时我们就可以换一个角度，把新结点都插入到最后，这种算法称为尾插法。

/* 尾插法创建单链表 */
void CreateListTail(LinkList *L)
{
    ElemType e;
    LinkList p, r;
    int i = 1;

    *L = (LinkList)malloc(sizeof(Node));
    r = *L;     // 使用 r 指向链表的尾部 NULL
    printf("输入表中的数据元素，输入 -100 结束!\n");
    while(i)
    {
        scanf("%d", &e);
        if(e == -100)   // 当输入 -100 时，判断输入结束，结束循环
            i = 0;
        else
        {
            p = (LinkList)malloc(sizeof(Node)); // 申请新结点空间
            p->data = e;    // 将输入的数据存入到申请的结点空间域
            r->Next = p;
            r = p;  // r=p 后 r->next 相当于再次指向了 NULL
        }
        r->Next = NULL;
    }
}

点链表的整表删除

当不打算再使用这个点链表时，就需要把整个表给销毁了，也就是在内存中将其释放，以便于节省空间，在上面的删除元素，我们释放的只是单个结点的内存空间。

单链表整表删除的算法思路如下：

1. 声明结点 p 和 q；
2. 将第一个结点赋值给 p，下一个节点赋值给 q；
3. 循环执行释放 p，释放后将 q 赋值给 p 的操作。

/* 删除整表 */
Status ClearList(LinkList *L)
{
    LinkList p, q;

    p = (*L)->Next; // p 指向头结点

    while(p)    // p 有数据就为真
    {
        q = p->Next;// q 指向 p 的下一个结点
        free(p);    // 释放 p
        p = q;      // 释放后的 p 为空，将 q（也就是之前的 p->next） 赋值给 p
    }
    (*L)->Next = NULL;  // 最后为空表

    return OK;
}

单链表打印

/* 打印表 */
void PrintList(LinkList L)
{
    LinkList p;
    p = L->Next;
    printf("L->");

    while(p)
    {
        printf(" %d->", p->data);
        p = p->Next;
    }
    printf("NULL\n");
}

测试代码

int main()
{
    /* 选择子函数 */
    int select()
    {
        int s;
        printf("输入要操作的序号：\n------------------------------\n");
        printf("1. 单链表建立（头插法）\n");
        printf("2. 单链表建立（尾插法）\n");
        printf("3. 单链表结点插入\n");
        printf("4. 单链表结点删除\n");
        printf("5. 单链表打印\n");
        printf("6. 单链表整表删除\n");
        printf("0. 退出\n------------------------------\n");

        for(;;)
        {
            scanf("%d", &s);
            if(s < 0 || s > 6)
                printf("输入错误，重新输入！");
            else
                break;
        }
        return s;
    }

    LinkList L;
    ElemType e;
    int i;

    for(;;)
    {
        switch(select())
        {
        case 1:
            printf("单链表建立（头插法）\n");
            CreateListHead(&L);
            break;
        case 2:
            printf("单链表建立（尾插法）\n");
            CreateListTail(&L);
            break;
        case 3:
            printf("单链表结点插入\n");
            printf("输入要插入的位置：");
            scanf("%d", &i);
            printf("输入要插入的元素：");
            scanf("%d", &e);
            if(InsertElem(L, i, e) == OK)
                printf("插入成功！\n");;
            break;
        case 4:
            printf("单链表结点删除\n");
            printf("输入要删除元素的位置：");
            scanf("%d", &i);
            if(DeleteElem(&L, i, &e) == OK)
                printf("\n删除的元素为 %d\n", e);
            break;
        case 5:
            printf("单链表打印如下：\n");
            PrintList(L);
            break;
        case 6:
            printf("单链表整表删除\n");
            if(ClearList(&L) == OK)
                printf("删除成功！\n");
            break;
        case 0:
            printf("再见！\n");
            return 0;
        }
    }
    return 0;
}

单链表结构与顺序存储结构的优缺点

存储分配方式

• 顺序存储结构用一段连续的存储单元依次存储线性表的数据元素
• 单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素

时间性能

1. 查找

• 顺序存储结构 O(1)
• 单链表 O(n)

2. 插入和删除

• 顺序存储结构需要平均移动表长一半的元素，时间为 O(n)
• 单链表在计算出某位置的指针后，插入和删除的时间仅为 O(1)

3. 空间性能

• 顺序存储结构需要事先分配存储空间，分大了，容易造成空间浪费，分小了，容易发生溢出
• 单链表不需要分配存储空间，进行动态分配，有一个分配一个，元素的个数也不受限制

综上所述，得出结论：

• 若线性表需要频繁进行查找，很少进行插入和删除的操作，适合采用顺序存储结构
• 若需要频繁插入和删除，适合采用单链表结构

例如：

• 在游戏开发中，对于用户注册的个人信息，除了注册时插入数据外，绝大多数情况都是读取，所以应考虑采用顺序存储结构
• 而游戏中武器或者装备列表，随着玩家在游戏过程中的增加或删除，此时采用单链表结构较为适合
• 当线性表中的元素个数变化较大或者根本不知道有多大时，最好采用单链表结构，这样不需要考虑存储空间大小的问题
• 如果事先知道线性表的大致长度，例如：一年的 12 个月，一周的七天等，这种采用顺序存储结构效率会高很多。