cf div2 #444 (ABC)(D已补)
ABC三道大水题,自信满满锁了溜出自习室回寝睡觉,第二天起来发现变成两道题了,哭唧唧。
回头翻代码吃了一口大翔,少写了两行被自己gank了。
然后由于出题人的数据放错了导致D题一开始没人过,E和F零星有几个人,然后就洒富富跑去开F和E,数据改了重判之后D题人数飙升但是没什么时间了(一定是出题人的锅)。
好吧怪自己没把题目都看一遍,盲目跟榜会吃翔的,以后记得不管什么比赛都尽可能把所有题目都看一遍。
A. Div. 64:
给你一串1和0,问你能否删去部分数字使其转换为10进制后能被64整除。
题意翻译过来就是问你能不能在这一串0和1中找出一个非连续子串1000000,能找到即可。
AC代码:
#include
#include
#include
using namespace std;
int main(void){
char str[105] ;
scanf ("%s", str );
int l = strlen(str) ;
int num = 0 , flag = 0 ;
for ( int i = 0 ; i < l ; i ++ ){
if ( str[i] == '1' ){
flag = 1 ;
}
if ( str[i] == '0' && flag == 1 ){
num ++ ;
}
if ( num == 6 ){
break ;
}
}
if ( num == 6 ){
printf ("yes\n");
} else {
printf ("no\n");
}
return 0;
} B. Cubes for Masha:
给你1到3个骰子,每个上面写着0-9其中的六个数字,问你从1开始能取到的最大数是多少(不需要用上所有骰子),比如手中有一个骰子,写着1 2 3 4 5 6,则最大不能取到的是6,两个骰子分别写着0 1 2 3 4 5 , 6 7 8 9 1 2,则最小不能取到的是29(0 1 2 3 4 5 6 7 8 9分别可以由一个骰子得到,10 可以由第二个骰子的1和第一个骰子的0得到,以此类推)。
考虑到三个骰子最多三位数,直接暴力开一个1005的整形数组num,把所有可能情况都跑一遍记录在num中,然后在num中找一个最小的找不到的数,那这个数的前一个就是最大的找得到的数。
AC代码:
#include
#include
using namespace std;
int main(void){
int num[1005] = {} , cube[3][8] ;
int n ;
scanf ("%d", &n );
for ( int i = 0 ; i < n ; i ++ ){
for ( int j = 0 ; j < 6 ; j ++ ){
scanf ("%d", &cube[i][j] );
}
}
if ( n == 1 ){
for ( int i = 0 ; i < 6 ; i ++ ){
num[cube[0][i]] = 1 ;
}
} else if ( n == 2 ){
for ( int i = 0 ; i < 6 ; i ++ ){
num[cube[0][i]] = 1 ;
num[cube[1][i]] = 1 ;
}
for ( int i = 0 ; i < 6 ; i ++ ){
for ( int j = 0 ; j < 6 ; j ++ ){
num[cube[0][i]*10+cube[1][j]] = 1 ;
num[cube[0][j]*10+cube[1][i]] = 1 ;
num[cube[1][j]*10+cube[0][i]] = 1 ; //PP代码这一句和下一句没写,导致赛后wa82 一大口shit
num[cube[1][j]*10+cube[0][i]] = 1 ;
}
}
} else if ( n == 3 ){
for ( int i = 0 ; i < 6 ; i ++ ){
num[cube[0][i]] = 1 ;
num[cube[1][i]] = 1 ;
num[cube[2][i]] = 1 ;
}
for ( int i = 0 ; i < 6 ; i ++ ){
for ( int j = 0 ; j < 6 ; j ++ ){
num[cube[0][i]*10+cube[1][j]] = 1 ;
num[cube[0][i]*10+cube[2][j]] = 1 ;
num[cube[1][i]*10+cube[0][j]] = 1 ;
num[cube[1][i]*10+cube[2][j]] = 1 ;
num[cube[2][i]*10+cube[0][j]] = 1 ;
num[cube[2][i]*10+cube[1][j]] = 1 ;
}
}
for ( int i = 0 ; i < 6 ; i ++ ){
for ( int j = 0 ; j < 6 ; j ++ ){
for ( int k = 0 ; k < 6 ; k ++ ){
num[cube[0][i]*100+cube[1][j]*10+cube[2][k]] = 1 ;
num[cube[0][i]*100+cube[2][j]*10+cube[1][k]] = 1 ;
num[cube[1][i]*100+cube[0][j]*10+cube[2][k]] = 1 ;
num[cube[1][i]*100+cube[2][j]*10+cube[0][k]] = 1 ;
num[cube[2][i]*100+cube[0][j]*10+cube[1][k]] = 1 ;
num[cube[2][i]*100+cube[1][j]*10+cube[0][k]] = 1 ;
}
}
}
}
for ( int i = 1 ; i < 1005 ; i ++ ){
if ( num[i] == 0 ){
printf ("%d\n", i-1 );
break ;
}
}
return 0;
} C. Solution for Cube:
给你一个2*2*2的二阶魔方,给你24个数字,分别表示六个面上每个格子的颜色,问你这个魔方能否由一次旋转变为一个拼好了的魔方(必须转一次)。
(出题人甚至给错了例1的配图)
题目中的样例2输入为:
5 3 5 3 2 5 2 5 6 2 6 2 4 4 4 4 1 1 1 1 6 3 6 3对应下图:
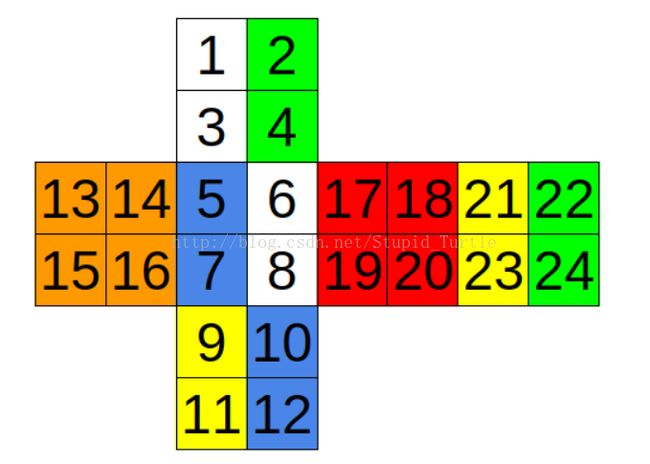
1-24所对应的方格是确定的。
思路:首先在输入时判断这个魔方有几个面已经拼好了,记录拼好的面的个数以及拼好的是哪一个面。
如果拼好的面不足两个或多于两个,必定不能由一次旋转得到拼好的魔方。
如果拼好的面为两个,则再判断拼好的两个面是否为相互面对的面(相互面对的面没有边或点连接),如果相互面对则一顿暴力的判断。
AC代码:
#include
#include
#include
using namespace std;
int main(void){
int a[26] = {} , flag[6] = {} , cnt = 0 ;
for ( int i = 0 ; i < 6 ; i ++ ){
for ( int j = 1 ; j <= 4 ; j ++ ){
scanf ("%d", &a[i*4+j] );
}
if ( a[i*4+1] == a[i*4+2] && a[i*4+1] == a[i*4+3] && a[i*4+1] == a[i*4+4] ){
flag[i] = 1 ;
cnt ++ ;
}
}
if ( cnt != 2 ){
printf ("NO\n");
} else {
if ( flag[0] && flag[2] ){
if ( ( a[5] == a[6] && a[5] == a[15] && a[5] == a[16] && a[7] == a[8] && a[7] == a[17] && a[7] == a[18] && a[19] == a[20] && a[19] == a[21] && a[19] == a[22] && a[13] == a[14] && a[13] == a[23] && a[13] == a[24] ) || ( a[7] == a[8] && a[7] == a[13] && a[7] == a[14] && a[5] == a[6] && a[5] == a[19] && a[5] == a[20] && a[17] == a[18] && a[17] == a[23] && a[17] == a[24] && a[21] == a[22] && a[21] == a[15] && a[21] == a[16] ) ){
printf ("YES\n");
} else {
printf ("NO\n");
}
} else if ( flag[1] && flag[5] ){
if ( ( a[1] == a[2] && a[1] == a[17] && a[1] == a[19] && a[9] == a[18] && a[9] == a[10] && a[9] == a[20] && a[12] == a[11] && a[11] == a[14] && a[11] == a[16] && a[3] == a[4] && a[3] == a[13] && a[3] == a[15] ) || ( a[4] == a[3] && a[3] == a[18] && a[3] == a[20] && a[11] == a[12] && a[11] == a[17] && a[11] == a[19] && a[9] == a[10] && a[9] == a[13] && a[9] == a[15] && a[1] == a[2] && a[1] == a[14] && a[1] == a[16] ) ){
printf ("YES\n");
} else {
printf ("NO\n");
}
} else if ( flag[3] && flag[4] ){
if ( ( a[1] == a[3] && a[1] == a[6] && a[1] == a[8] && a[5] == a[7] && a[5] == a[10] && a[5] == a[12] && a[9] == a[11] && a[9] == a[21] && a[9] == a[23] && a[2] == a[4] && a[2] == a[22] && a[2] == a[24] ) || ( a[1] == a[3] && a[1] == a[21] && a[1] == a[23] && a[2] == a[4] && a[2] == a[5] && a[2] == a[7] && a[9] == a[11] && a[9] == a[6] && a[9] == a[8] && a[10] == a[12] && a[10] == a[22] && a[10] == a[24] ) ){
printf ("YES\n");
} else {
printf ("NO\n");
}
} else {
printf ("NO\n");
}
}
return 0;
} 补题后会放上代码(虽然这么弱感觉补不了什么题,试试吧)。
---------------------------------------------补题分割线---------------------------------------------
D. Ratings and Reality Shows
一直wa4,没有找到原因,数据组数太多又不能调就没仔细看,所以骂了很久的数据。然后稍微仔细看了下,答案是0,我的输出是1,wori为什么输出可以是0,一大口shit。
题意:一个人要去参加一个比赛。比赛期间她有两个活动A和B,在给定的某一天进行其中一个活动(每天至多进行一个活动)。从第0天开始她可以举办一次演讲,在演讲之前,进行A活动会给她加上a分,进行B活动会给她减去b分;而在举办演讲之后,进行A活动会给她加上c分,进行B活动会给她减去d分,她的初始分数start给出,演讲活动的buff持续时间len也给出,问你:她最早可以在第几天举办演讲,来满足演讲之前和期间的总分都不会出现负数。
思路:尺取法,起始标记点s记录左端,终点标记点e记录右端,用一个sum维护初始的分数。若s点和e点之间的距离大于等于给定len,则判断初始分数加上过程中的最低分数是否满足大于等于0。若满足则直接输入,否则将初始分数sum加上左端s位置的对应分数(若s对应位置当天是加的则加上,减去的则减去),而最小值与sum相反,减去左端s的对应分数。若改变后的sum小于0,输出-1(因为要求在举办演讲之前的分数也要大于等于0,也是一个wa点)。
注意:左端s的初始点的左侧应为第-1天(即tag为-1),否则在第四组样例中你的输出也会为1而不是0(同为wa点)。
测试数据:
5 1 1 1 1 0 2
1 1
2 1
3 1
4 1
5 1
你的输出应该为0而不是1。
AC代码:
#include
#include
#include
using namespace std;
typedef long long ll ;
struct node {
int q , t ;
};
node pos[300005] ;
int main(void){
ll n , a , b , c , d , st , len ;
scanf ("%I64d%I64d%I64d%I64d%I64d%I64d%I64d",&n,&a,&b,&c,&d,&st,&len );
for ( int i = 1 ; i <= n ; i ++ ){
scanf ("%d%d",&pos[i].q,&pos[i].t );
}
ll sum = st , ans = 0 , minn = 0 ;
int e = 1 ;
pos[0].q = -1 ;
for ( int s = 1 ; s <= n ; s ++ ){
while ( e <= n && pos[e].q - pos[s].q <= len ){
if ( pos[e].t == 1 ){
ans += c ;
} else {
ans -= d ;
}
minn = min ( minn , ans );
e ++ ;
}
if ( sum + minn >= 0 ){
printf ("%d\n", pos[s-1].q + 1 );
return 0 ;
}
if ( pos[s].t == 1 ){
ans -= c ;
minn -= c ;
sum += a ;
} else {
ans += d ;
minn += d ;
sum -= b ;
}
if ( sum < 0 ){
printf ("-1\n");
return 0;
}
}
printf ("%d\n", pos[n].q + 1 );
return 0;
}