winograd 卷积计算加速

论文：https://arxiv.org/pdf/1509.09308.pdf
论文PPT
参考腾讯开源的NNCN对winograd的实现，NCNN的开源地址。

一维F(2,3)实现代码：

# 论文地址 https://arxiv.org/abs/1509.09308
import numpy

x0 = 1
x1 = 2
x2 = 3
x3 = 4
x = numpy.matrix([[x0, x1, x2],[x1, x2, x3]])

w0 = 7
w1 = 8
w2 = 9
w = numpy.matrix([w0, w1, w2]).T
# 普通的x*w^T 矩阵乘法, 乘法的次数 2*3 = 6次，6次加法
y = x*w
print(y)


# 一维winograd, 4次乘法， 8次加法 ，跟w相关的加减乘除可以在初始化的时候
# 计算好，所以不占用计算量
# µ(F(m, r)) = m + r - 1
m1 = (x0 - x2) * w0
m2 = (x1 + x2) * (w0 + w1 + w2)/2
m4 = (x1 - x3) * w2
m3 = (x2 - x1) * (w0 - w1 + w2) /2

y = numpy.matrix([m1+m2+m3, m2-m3-m4]).T
print(y)

扩展到2D

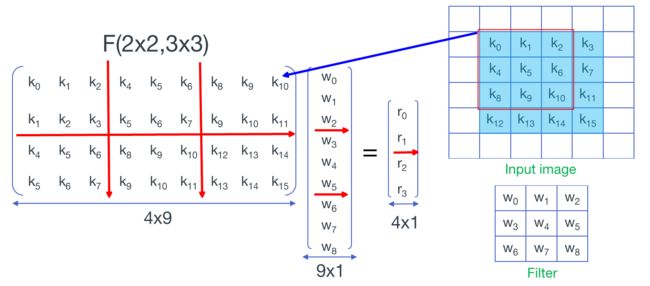
将卷积核的元素拉成一列，将输入信号每个滑动窗口中的元素拉成一行。注意图中红线划分成的分块矩阵，每个子矩阵中重复元素的位置与一维时相同，同时重复的子矩阵也和一维时相同。

图片出自论文Sparse Winograd Convolutional neural networks on small-scale systolic arrays

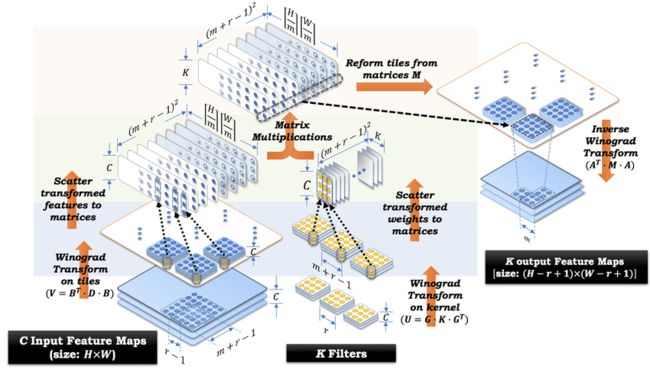
linux x86上面的实现，主要的入口在convolution_x86.h文件

int Convolution_x86::create_pipeline(const Option& opt) {

}