MLSys 2020 | FedProx:异质网络的联邦优化
目录
- 前言
- I. FedAvg
- II. FedProx
- III. 实验
- IV. 总结
前言

题目: Federated Optimization for Heterogeneous Networks
会议: Conference on Machine Learning and Systems 2020
论文地址:Federated Optimization for Heterogeneous Networks
FedAvg对设备异质性和数据异质性没有太好的解决办法,FedProx在FedAvg的基础上做出了一些改进来尝试缓解这两个问题。
在Online Learning中,为了防止模型根据新到来的数据进行更新后偏离原来的模型太远,也就是为了防止过调节,通常会加入一个余项来限制更新前后模型参数的差异。FedProx中同样引入了一个余项,作用类似。
I. FedAvg
Google的团队首次提出了联邦学习,并引入了联邦学习的基本算法FedAvg。问题的一般形式:

公式1: f i ( w ) = l ( x i , y i ; w ) f_i(w)=l(x_i,y_i;w) fi(w)=l(xi,yi;w)表示第 i i i个样本的损失,即最小化所有样本的平均损失。
公式2: F k ( w ) F_k(w) Fk(w)表示一个客户端内所有数据的平均损失, f ( w ) f(w) f(w)表示当前参数下所有客户端的加权平均损失。
值得注意的是,如果所有 P k P_k Pk(第k个客户端的数据)都是通过随机均匀地将训练样本分布在客户端上来形成的,那么每一个 F k ( w ) F_k(w) Fk(w)的期望都为 f ( w ) f(w) f(w)。这通常是由分布式优化算法做出的IID假设:即每一个客户端的数据相互之间都是独立同分布的。
FedAvg:
![]()
简单来说,在FedAvg的框架下:每一轮通信中,服务器分发全局参数到各个客户端,各个客户端利用本地数据训练相同的epoch,然后再将梯度上传到服务器进行聚合形成更新后的参数。
FedAvg存在着两个缺陷:
- 设备异质性:不同的设备间的通信和计算能力是有差异的。在FedAvg中,被选中的客户端在本地都训练相同的epoch,虽然作者指出提升epoch可以有效减小通信成本,但较大的epoch下,可能会有很多设备无法按时完成训练。无论是直接drop掉这部分客户端的模型还是直接利用这部分未完成的模型来进行聚合,都将对最终模型的收敛造成不好的影响。
- 数据异质性:不同设备中数据可能是非独立同分布的。如果数据是独立同分布的,那么本地模型训练较多的epoch会加快全局模型的收敛;如果不是独立同分布的,不同设备在利用非IID的本地数据进行训练并且训练轮数较大时,本地模型将会偏离初始的全局模型。
II. FedProx
为了缓解上述两个问题,本文作者提出了一个新的联邦学习框架FedProx。FedProx能够很好地处理异质性。
定义一:

所谓 γ \gamma γ inexact solution:对于一个待优化的目标函数 h ( w ; w 0 ) h(w;w_0) h(w;w0),如果有:
∣ ∣ ∇ h ( w ∗ ; w 0 ) ∣ ∣ ≤ γ ∣ ∣ ∇ h ( w 0 ; w 0 ) ∣ ∣ ||\nabla h(w^*;w_0)|| \leq \gamma ||\nabla h(w_0;w_0)|| ∣∣∇h(w∗;w0)∣∣≤γ∣∣∇h(w0;w0)∣∣
这里 γ ∈ [ 0 , 1 ] \gamma \in [0,1] γ∈[0,1],我们就说 w ∗ w^* w∗是 h h h的一个 γ − \gamma- γ−不精确解。
对于这个定义,我们可以理解为:梯度越小越精确,因为梯度越大,就需要更多的时间去收敛。那么很显然, γ \gamma γ越小,解 w ∗ w^* w∗越精确。
我们知道,在FedAvg中,设备 k k k在本地训练时,需要最小化的目标函数为:
F k ( w ) = 1 n k ∑ i ∈ P k f i ( w ) F_k(w)=\frac{1}{n_k}\sum_{i \in P_k}f_i(w) Fk(w)=nk1i∈Pk∑fi(w)
简单来说,每个客户端都是优化所有样本的损失和,这个是正常的思路,让全局模型在本地数据集上表现更好。
但如果设备间的数据是异质的,每个客户端优化之后得到的模型就与初始时服务器分配的全局模型相差过大,本地模型将会偏离初始的全局模型,这将减缓全局模型的收敛。
为了有效限制这种偏差,本文作者提出,设备 k k k在本地进行训练时,需要最小化以下目标函数:
h k ( w ; w t ) = F k ( w ) + μ 2 ∣ ∣ w − w t ∣ ∣ 2 h_k(w;w^t)=F_k(w)+\frac{\mu}{2}||w-w^t||^2 hk(w;wt)=Fk(w)+2μ∣∣w−wt∣∣2
作者在FedAvg损失函数的基础上,引入了一个proximal term,我们可以称之为近端项。引入近端项后,客户端在本地训练后得到的模型参数 w w w将不会与初始时的服务器参数 w t w^t wt偏离太多。
观察上式可以发现,当 μ = 0 \mu=0 μ=0时,FedProx客户端的优化目标就与FedAvg一致。
这个思路其实还是很常见的,在机器学习中,为了防止过调节,亦或者为了限制参数变化,通常都会在原有损失函数的基础上加上这样一个类似的项。比如在在线学习中,我们就可以添加此项来限制更新前后模型参数的差异。
FedProx的算法伪代码:

输入:客户端总数 K K K、通信轮数 T T T、 μ \mu μ和 γ \gamma γ、服务器初始化参数 w 0 w^0 w0,被选中的客户端的个数 N N N,第 k k k个客户端被选中的概率 p k p_k pk。
对每一轮通信:
- 服务器首先根据概率 p k p_k pk随机选出一批客户端,它们的集合为 S t S_t St。
- 服务器将当前参数 w t w^t wt发送给被选中的客户端。
- 每一个被选中的客户端需要寻找一个 w k t + 1 w_k^{t+1} wkt+1,这里的 w k t + 1 w_k^{t+1} wkt+1不再是FedAvg中根据本地数据SGD优化得到的,而是优化 h k ( w ; w t ) h_k(w;w^t) hk(w;wt)后得到的 γ − \gamma- γ−不精确解。
- 每个客户端将得到的不精确解传递回服务器,服务器聚合这些参数得到下一轮初始参数。
通过观察这个步骤可以发现,FedProx在FedAvg上做了两点改进:
- 引入了近端项,限制了因为数据异质性导致的模型偏离。
- 引入了不精确解,各个客户端不再需要训练相同的轮数,只需要得到一个不精确解,这有效缓解了某些设备的计算压力。
III. 实验
图1给出了数据异质性对模型收敛的影响:
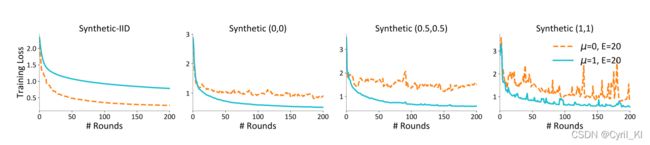
上图给出了损失随着通信轮数增加的变化情况,数据的异质性从左到右依次增加,其中 μ = 0 \mu=0 μ=0表示FedAvg。可以发现,数据间异质性越强,收敛越慢,但如果我们让 μ > 0 \mu>0 μ>0,将有效缓解这一情况,也就是模型将更快收敛。
图2:
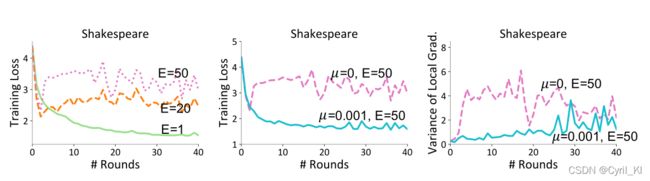
左图:E增加后对 μ = 0 \mu=0 μ=0情况的影响。可以发现,太多的本地训练将导致本地模型偏离全局模型,全局模型收敛变缓。
中图:同一数据集,增加 μ \mu μ后,收敛将加快,因为这有效缓解了模型的偏移,从而使FedProx的性能较少依赖于 E E E。
作者给出了一个trick:在实践中, μ \mu μ可以根据模型当前的性能自适应地选择。比较简单的做法是当损失增加时增加 μ \mu μ,当损失减少时减少 μ \mu μ。
但是对于 γ \gamma γ,作者貌似没有具体说明怎么选择,只能去GitHub上研究一下源码再给出解释了。
IV. 总结
数据和设备的异质性对传统的FedAvg算法提出了挑战,本文作者在FedAvg的基础上提出了FedProx,FedProx相比于FedAvg主要有以下两点不同:
- 考虑了不同设备通信和计算能力的差异,并引入了不精确解,不同设备不需要训练相同的轮数,只需要得到一个不精确解即可。
- 引入了近端项,在数据异质的情况下,限制了本地训练时模型对全局模型的偏离。