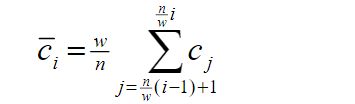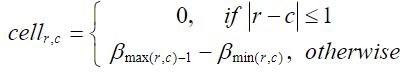SAX（Symbolic Aggregate Approximation ）：时间序列的符号化表示（附Python3代码，包括距离计算）

   SAX全称 Symbolic Aggregate Approximation， 中文意思是符号近似聚合，简单的说是一种把时间序列进行符号化表示的方法。

SAX的基本步骤如下：

（1）将原始时间序列规格化，转换成均值为0，标准差为1 的的序列，原论文中解释的原因如下：

       

        

（2）通过PAA(Piecewise Aggregate Approximation)进行降维，将长为 n 的原始时间序列 = ,  ,..., 转换长为 w 的序列=,,...,。

简单的说，PAA就是先把原始序列分成等长的 w 段子序列，然后用每段子序列的均值来代替这段子序列。 

PAA降维的公式如下：

                                            

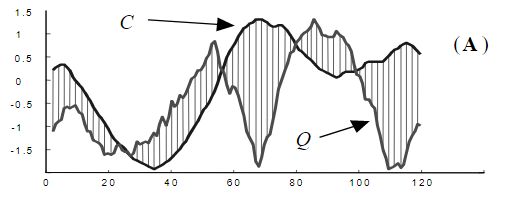
转换后的图如下：

                                 

（3）符号化表示。先选定字母集的大小α, （就是你想用多少个字母来表示整个时间序列，比如选三个字母‘a’, 'b', 'c'，则α=3）

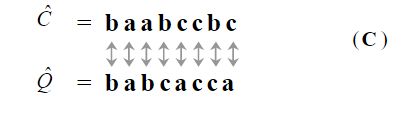
然后在下面的表格中查找区间的分裂点，将PAA表示的均值映射为相应的字母，最终离散化为字符串

                                  

符号化之后的图：

                                     

这样原始的时间序列就离散化为字符串：baabccbc

符号化后的时间序列间的距离计算：

给定两个长度都为 n 时间序列 Q 和 C，则序列Q和序列C之间的欧式距离可以用下面计算：

                                                   

两个原始时间序列的距离：

                                     

当时间序列 Q 和 C 经过PAA降维之后，变成和，时间序列的欧式距离计算公式如下：（此公式计算的是两个原始时间序列之间的欧氏距离的下边界近似值，关于下界定理和下边界紧凑性的说明在博客：下界（lower bounding）定理和下界紧密性比较）

                                              

 

此时计算的距离是：

                                        

经过符号化之后，时间序列 Q  和 C 变成  和 ，欧式距离的计算公式为：（两个原始时间序列之间的最小距离）                                              

此时计算的距离为：

 

                                               

公式中的dist()函数可以从距离表中查到，比如我们选的字母集的大小为4的时候距离表如下：

                                          

此时 dist(a, b)=0,  dist(a, c)=0.67

注意：不同的字母集大小的距离表不同。

距离表中每个单元格的值可以由一下公式计算：

                                       

公式中的  的值是在第二步中的表中。

 

代码如下

import numpy as np
import math

class SAX_trans:
    
    def __init__(self, ts, w, alpha):
        self.ts = ts
        self.w = w
        self.alpha = alpha
        self.aOffset = ord('a') #字符的起始位置，从a开始
        self.breakpoints = {'3' : [-0.43, 0.43],
                            '4' : [-0.67, 0, 0.67],
                            '5' : [-0.84, -0.25, 0.25, 0.84],
                            '6' : [-0.97, -0.43, 0, 0.43, 0.97],
                            '7' : [-1.07, -0.57, -0.18, 0.18, 0.57, 1.07],
                            '8' : [-1.15, -0.67, -0.32, 0, 0.32, 0.67, 1.15],
            
        }
        self.beta = self.breakpoints[str(self.alpha)]
        
    def normalize(self):  # 正则化
        X = np.asanyarray(self.ts)
        return (X - np.nanmean(X)) / np.nanstd(X)

    def paa_trans(self):  #转换成paa
        tsn = self.normalize() # 类内函数调用：法1：加self：self.normalize()   法2：加类名：SAX_trans.normalize(self) 
        paa_ts = []
        n = len(tsn)
        xk = math.ceil( n / self.w )  #math.ceil()上取整，int()下取整
        for i in range(0,n,xk):
            temp_ts = tsn[i:i+xk]
            paa_ts.append(np.mean(temp_ts))
            i = i + xk
        return paa_ts
    
    def to_sax(self):   #转换成sax的字符串表示
        tsn = self.paa_trans()
        len_tsn = len(tsn)
        len_beta = len(self.beta)
        strx = ''
        for i in range(len_tsn):
            letter_found = False
            for j in range(len_beta):
                if np.isnan(tsn[i]):
                    strx += '-'
                    letter_found = True
                    break                   
                if tsn[i] < self.beta[j]:
                    strx += chr(self.aOffset +j)
                    letter_found = True
                    break
            if not letter_found:
                strx += chr(self.aOffset + len_beta)
        return strx
    
    
    def compare_Dict(self):   # 生成距离表 
        num_rep = range(self.alpha)  #存放下标
        letters = [chr(x + self.aOffset) for x in num_rep]   #根据alpha，确定字母的范围
        compareDict = {}
        len_letters = len(letters)
        for i in range(len_letters):
            for j in range(len_letters):
                if np.abs(num_rep[i] - num_rep[j])<=1:
                    compareDict[letters[i]+letters[j]]=0
                else:
                    high_num = np.max([num_rep[i], num_rep[j]])-1
                    low_num = np.min([num_rep[i], num_rep[j]])
                    compareDict[letters[i]+letters[j]] = self.beta[high_num] - self.beta[low_num]
        return compareDict
   
    def dist(self, strx1,strx2):   #求出两个字符串之间的mindist()距离值
        len_strx1 = len(strx1)
        len_strx2 = len(strx2)
        com_dict = self.compare_Dict()

        if len_strx1 != len_strx2:
            print("The length of the two strings does not match")
        else:
            list_letter_strx1 = [x for x in strx1]
            list_letter_strx2 = [x for x in strx2]
            mindist = 0.0
            for i in range(len_strx1):
                if list_letter_strx1[i] is not '-' and list_letter_strx2[i] is not '-':
                    mindist += (com_dict[list_letter_strx1[i] + list_letter_strx2[i]])**2
            mindist = np.sqrt((len(self.ts)*1.0)/ (self.w*1.0)) * np.sqrt(mindist)
            return mindist
  
                    
# 测试            
ts1 = [6.02, 6.33, 6.99, 6.85, 9.20, 8.80, 7.50, 6.00, 5.85, 3.85, 6.85, 3.85, 2.22, 1.45, 4.34,
      5.50, 1.29, 2.58, 3.83, 3.25, 6.25, 3.83, 5.63, 6.44, 6.25, 8.75, 8.83, 3.25, 0.75, 0.72]

ts2 = [0.50, 1.29, 2.58, 3.83, 3.25, 4.25, 3.83, 5.63, 6.44, 6.25, 8.75, 8.83, 3.25, 0.75, 0.72,
      2.02, 2.33, 2.99, 6.85, 9.20, 8.80, 7.50, 6.00, 5.85, 3.85, 6.85, 3.85, 2.22, 1.45, 4.34,]
x1 = SAX_trans(ts=ts1,w=6,alpha=3)
x2 = SAX_trans(ts=ts2,w=6,alpha=3)
st1 = x1.to_sax()
st2 = x2.to_sax()
dist = x1.dist(st1,st2)
print('st1',st1)
print('st2',st2)
print(dist)
            
        

输出如下：

               

Reference:

Lin J , Keogh E J , Lonardi S , et al. A Symbolic Representation of Time Series, with Implications for Streaming Algorithms[C]// Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery, DMKD 2003, San Diego, California, USA, June 13, 2003. ACM, 2003.

SAX (Symbolic Aggregate Approximation) 一种时间序列的新型符号化方法

SAX（Symbolic Aggregate Approximation

https://github.com/nphoff/saxpy/blob/master/saxpy.py

---

。。。