Python 的一些统计函数 Scipy

看 Python 量化金融投资，摘录的一些统计函数。为了以后更好的查找。

import numpy as np
import numpy.linalg as nlg
import scipy.stats as stats 
import scipy.optimize as opt
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
plt.rcParams['font.sans-serif'] = ['FangSong'] # 设置中文
plt.rcParams['axes.unicode_minus'] = False # 设置中文负号
plt.style.use('bmh')

统计工具

随机数

• 生成 n 个随机数 random variables rvs

• 连续型的随机数

  • rv_continuous.rvs(size=n)
  • 均匀分布 uniform
  • 正态分布 norm
  • $\beta$ 分布 beta
  • 等

• 离散型的随机数

  • rv.discrete.rvs(size=n)
  • 伯努利分布 bernoulli
  • 几何分布 geom
  • 泊松分布 poisson
  • 等

• 例：

stats.uniform.rvs(size=10)

array([0.90782979, 0.08204289, 0.82901539, 0.19884267, 0.50562515,
       0.82687688, 0.1920613 , 0.23374013, 0.45629651, 0.32507933])

np.random.seed(seed=2020)
stats.beta.rvs(size=10,a=4,b=2)

array([0.40765989, 0.81432442, 0.81389925, 0.925416  , 0.77791256,
       0.71965217, 0.76665344, 0.80133481, 0.72746346, 0.82444686])

• 也可

np.random.seed(seed=2020)
beta = stats.beta(a=4,b=2)
beta.rvs(size=10)

array([0.40765989, 0.81432442, 0.81389925, 0.925416  , 0.77791256,
       0.71965217, 0.76665344, 0.80133481, 0.72746346, 0.82444686])

假设检验

K-S 检验

• Kolmogorov-Smirnov test
• kstest
• 单样本 K-S 检验的原假设是 给定的数据来自和原假设相同的分布
• 基于累积分布函数，用以检验一个经验分布是否符合某种理论分布或比较两个经验分布是否有显著性差异。参考来源

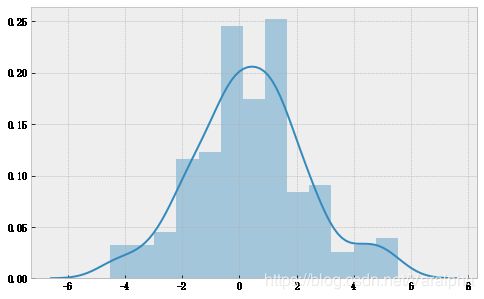
# 创建模拟正态分布数据
data = stats.norm.rvs(size=200,loc=0.5,scale=2)
mu = np.mean(data)
sigma = np.std(data)
print(f'Mean: {mu:.2f}\n\
Median: {np.median(data):.2f}\n\
Standard Deviation: {sigma:.2f}')
plt.figure(figsize=(8,5))
sns.distplot(data)
plt.show()

Mean: 0.39
Median: 0.29
Standard Deviation: 1.99

# 使用 KS-test
stat_val, p_val = stats.kstest(data,'norm',(mu,sigma))
print(f'KS-statistic D = {stat_val:.4f}\n\
p-value = {p_val:.4f}')

KS-statistic D = 0.0502
p-value = 0.7065

• p_value 表示显著水平（significance level），用于判断假设是否成立的依据。
• p_value 是服从 $[0,1]$ 区间上的正态分布随机变量。
• 在此例中 p_value 很大，因此接受原假设，该数据通过了正态性的检验。

T 检验

• T-test
• 在正态性的前提下，可进一步检验这组数据的均值是不是0.
• 典型的方法为 T-test
• ttest_1samp 单样本的 t 检验函数
• 单一样本的t检验，检验单一样本是否与给定的均值popmean差异显著的函数，第一个参数为给定的样本，第二个函数为给定的均值popmean，可以以列表的形式传输多个单一样本和均值。

stat_val, p_val = stats.ttest_1samp(data, 0) 
print(f'1-sample T_test -statistic D = {stat_val:.4f}\n\
p-value = {p_val:.4f}')

1-sample T_test -statistic D = 2.7951
p-value = 0.0057

• P_value < 0.05

• 在给定显著性水平 0.05 的前提下，应拒绝原假设：数据的均值为 0。

• 其他 T test:

  • ttest_ind: 独立样本的T检验，检验两个样本的均值差异，该检验方法假定了样本的通过了F检验，即两个独立样本的方差相同
  • ttest_ind_from_stats: 检验两个样本的均值差异（同上），输出的参数两个样本的统计量，包括均值，标准差，和样本大小
  • ttest_rel: 配对T检验，检测两个样本的均值差异，输入的参数是样本的向量

• 再生成一组数据，尝试一下双样本 t 检验

data2 = stats.norm.rvs(size=100,loc=-.2,scale=1.2)
plt.figure(figsize=(8,5))
sns.distplot(data2)
plt.show()

stat_val, p_val = stats.ttest_ind(data,data2,equal_var=False) 
print(f'2-sample T_test -statistic D = {stat_val:.4f}\n\
p-value = {p_val:.4f}')

2-sample T_test -statistic D = 3.5436
p-value = 0.0005

• 这里生成的第二组数据样本大小，方差，和第一组均不等，在运用 t_test 时需要使用 韦尔奇 t_test (Welch’s t_test), 即指定 equal_var = False。
• 同样得到较小的 p_value, 在显著性水平 0.05 前提下，拒绝原假设，即数据均值不等。

其他函数

累计分布

• Cumulative distribution Function cdf
• 给定一个分布，求分位上的数值

g_dist = stats.gamma(a=2)
print('分位数：[2,4,5] ')
g_dist.cdf([2,4,5])

分位数：[2,4,5] 





array([0.59399415, 0.90842181, 0.95957232])

概率密度

• Probability density function pdf

print('概率：[25%,50%,95%] ')
g_dist.cdf([0.25,0.5,0.95])

概率：[25%,50%,95%] 





array([0.02649902, 0.09020401, 0.245855  ])

分布信息

• moment
• 给定一个分布，查看分布的矩阵信息
• 例查看 N(0,1) 的六阶原点矩

stats.norm.moment(6,loc=0,scale=1)

15.000000000895332

统计描述分析

• describe
• 对数据集的统计描述分析，（大小，极值，均值，方差，偏度，峰度）

info = stats.describe(data)
print(f'总描述:   {info}')
print(f'数据大小: {info[0]}')
print(f'最小值:   {info[1][0]:.4f}')
print(f'最大值:   {info[1][1]:.4f}')
print(f'平均值:   {info[2]:.4f}')
print(f'方差:     {info[3]:.4f}')
print(f'偏度:     {info[4]:.4f}')
print(f'峰度:     {info[5]:.4f}')

总描述:   DescribeResult(nobs=200, minmax=(-4.522642873211459, 5.541935059612814), mean=0.3935187131823762, variance=3.964408344885493, skewness=0.1567664342974578, kurtosis=0.2158753158144524)
数据大小: 200
最小值:   -4.5226
最大值:   5.5419
平均值:   0.3935
方差:     3.9644
偏度:     0.1568
峰度:     0.2159

极大似然估计

• 极大似然估计 Maximum Likelihood Estimate
• fit 可以得到对应分布参数的极大似然估计。
• 例：数据服从正态分布

norm_dist_data = stats.norm.rvs(size=100,loc=0,scale=1.8)
'均值：{:.4f}, 方差：{:.4f}'.format(*stats.norm.fit(norm_dist_data))

'均值：0.0516, 方差：1.7697'

线性关联程度

• pearsonr Pearson correlation coefficient
• spearmanr Spearman correlation coefficient
• 这两个相关系数 度量了两组数据的线性关联程度

exp_dist_data = stats.expon.rvs(size=100)
print('Pearson -相关性：{:.4f}, P-value：{:.4f}'.format(*stats.pearsonr(norm_dist_data,exp_dist_data)))
print('Spearman-相关性：{:.4f}, P-value：{:.4f}'.format(*stats.spearmanr(norm_dist_data,exp_dist_data)))

Pearson -相关性：0.0643, P-value：0.5248
Spearman-相关性：-0.0026, P-value：0.9796

• p_value 表示 原假设（两组数据不相关）下相关性的显著性。

线性回归

• 例

x = stats.chi2.rvs(3,size=50) # chi-squared
error = stats.norm.rvs(size=50,loc=0,scale=1.5)
y = 2.5 + 1.2*x + error
stats.linregress(x,y)

LinregressResult(slope=1.262568027049048, intercept=2.4399994448207343, rvalue=0.9310325019777308, pvalue=1.1890093549402353e-22, stderr=0.0714309380687254)

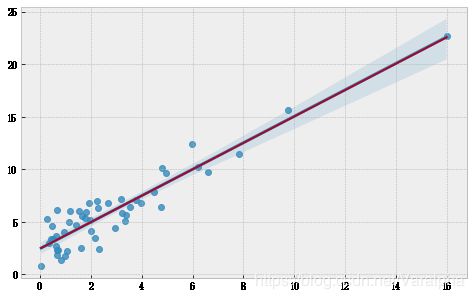
plt.figure(figsize=(8,5))
sns.regplot(x,y)
slope_y = x*1.26+2.44
sns.lineplot(x,slope_y)
plt.show()

• 可以看到 很方便得获得线性回归的各个数值。