MATLAB初入门(一)
我在这里使用的是MATLABR2014a,附上下载链接:https://pan.baidu.com/s/1Ro5o-4woFwe4qaGhDjJIlw 密码:1vb7。
安装好后下面开始我们的MATLAB之旅。
1.1离散时间信号的MATLAB表示
(1)离散时间信号的序列表示
例:
>>x=[-1,1,2,1,0,-1]; %离散时间信号x(n)序列幅度值
>>n=[-1,0,1,2,3,4]; %离散时间信号x(n)序列时间序列
两行合起来即为离散时间信号x(-1)=-1,x(0)=1,x(1)=2,x(2)=1,x(3)=0,x(4)=-1;
(2)离散时间信号的图形表示
这里将介绍stem这条专用函数命令
例:
>>n=-3:5;
>>x=[0,0,-1,1,2,1,-1,0,0];
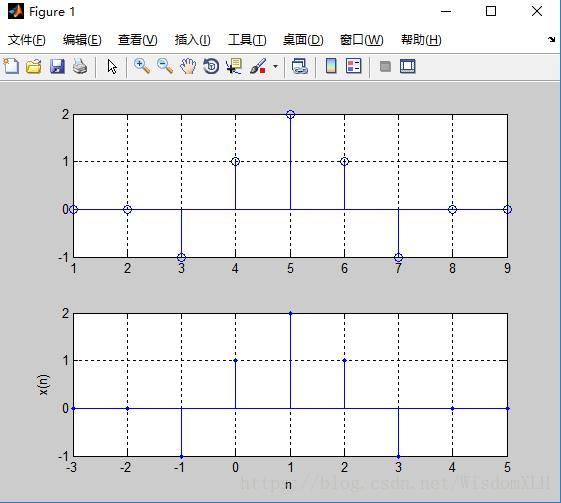
>>subplot(2,1,1),stem(x);
>>grid;line([1,9],[0,0]);
>>subplot(2,1,2);stem(n,x,'.');
>>grid;line([-3,5],[0,0]);
>>xlabel('n');ylabel('x(n)')
得到图形如下:
下面我们来逐条命令探索一下
>>n=-3:5;
>>x=[0,0,-1,1,2,1,-1,0,0];
这两行命令等价于x(-3)=0,x(-2)=0,x(-1)=-1,x(0)=1,x(1)=2,x(2)=1,x(3)=-1,x(4)=0,x(5)=0
可是第一个图却不是这样原因在于下面这一条命令
>>stem(x,'string'); %绘制x(n)的棒状图,横坐标为序列的下标序号,棒的末端由string指定,至于string有哪些,详见数字信号处理(第二版 唐向宏 编著)P315 表B-6
>>stem(n,x,'string'); %绘制x(n)的棒状图,横坐标由n指定
现在再来介绍一下subplot命令
>>subplot(m,n,p); %将图形窗口分成n*m个子图形窗口,并选择第p个子图形作为当前图形窗口
接下来是grid;line命令
gird;line(横坐标范围,x轴方向及其位置)
仍拿刚才的离散信号举例
例:
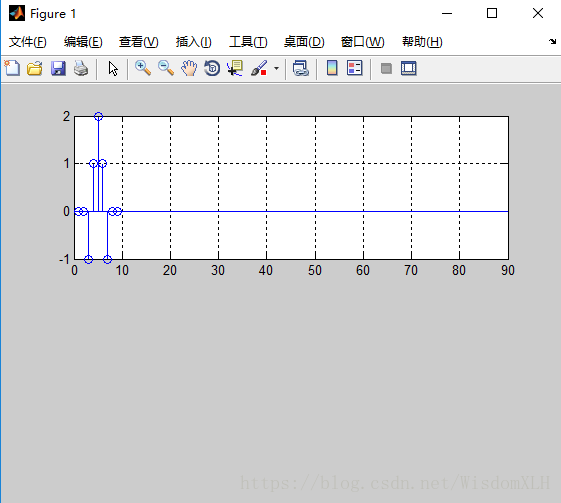
>>grid;line([0,90],[0,0]);
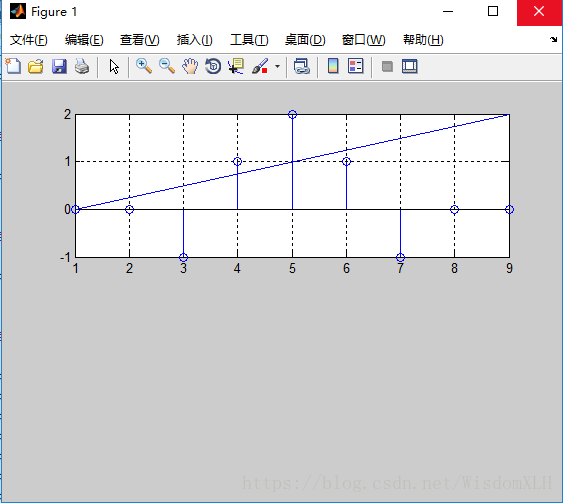
>>grid;line([1,9],[0,2])
最后再来介绍一下xlabel与ylabel
xlabel('n');ylabel('x(n)') %标注坐标轴
(3)常用离散信号的产生方法
令ns为序列的起始位置,nf为序列的终止位置。
(1)单位脉冲序列:δ(n-n0) = 1,n=n0;
0,n≠n0;
MATLAB命令:x=zeros(1,N);x(1,n0)=1;(其中N为序列个数)
(2)单位阶跃序列:u(n-n0)=1,n≥n0;
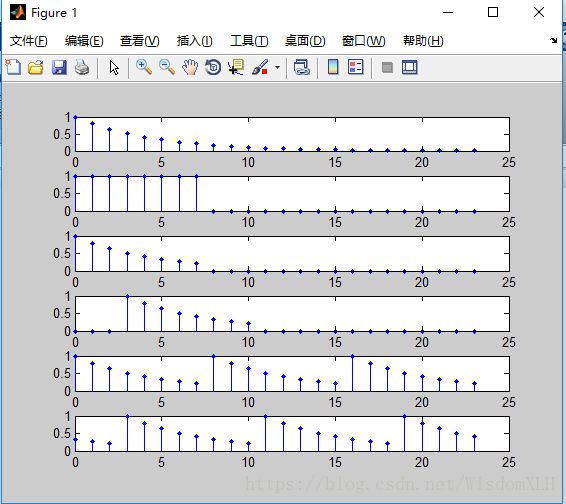
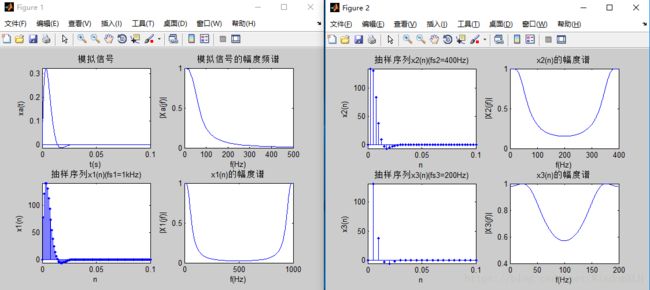
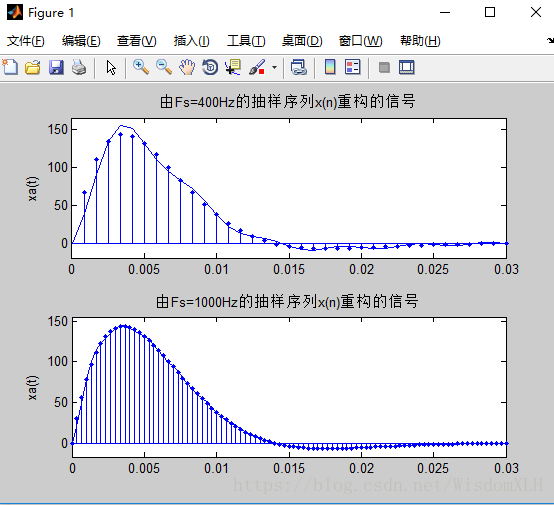
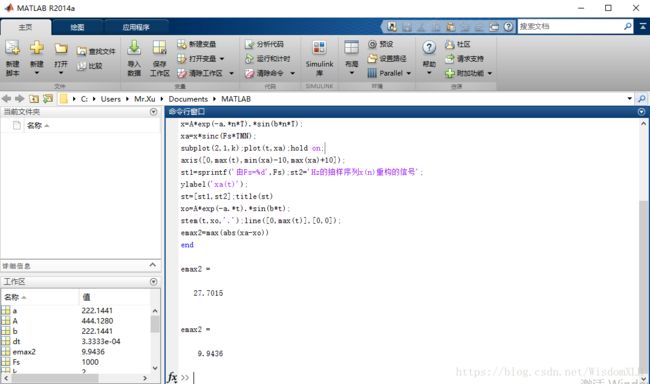
0,n MATLAB命令:n=[ns,:nf];x=[(n-n0)≥0]; (3)实指数序列:x(n)=a^n,(n,a∈R) MATLAB命令:n=[ns,:nf];x=a.^n; (4)复指数序列:x(n)=e^[(δ+jw)n],任意n MATLAB命令:n=[ns,:nf];x=exp((delta+jw)*n); (5)正(余)弦序列:x(n)=cos(wn+θ),任意n MATLAB命令:n=[ns,:nf];x=cos(w*n+sita); 1.2离散时间信号运算的实现 (1)信号的相加与相乘 方法:首先将两序列的时间变量延拓到同长,x1和x2分别成为y1和y2;然后再逐点相加y(n)=y1(n)+y2(n)或逐点相乘y(n)=y1(n)*y2(n),求得新信号。 例: n1=[-5:4]; n1s=-5;n1f=4; x1=[2,3,1,-1,3,4,2,1,-5,-3]; n2=[0:9]; n2s=0;n2f=9; x2=[1,1,1,1,1,1,1,1,1,1]; ns=min(n1s,n2s);nf=max(n1f,n2f); %求取新信号的时间起始及终止位置 n=ns:nf; y1=zeros(1,length(n)); y2=zeros(1,length(n)); %延拓序列初始化(两个单位脉冲序列) y1(find((n>=n1s)&(n<=n1f)==1))=x1; %给延陀序列y1赋值x1 y2(find((n>=n2s)&(n<=n2f)==1))=x2; %给延拓序列y2赋值x2 //这里介绍一下find函数的用法——找出所有非零元素,在这里即为函数定义域里的元素// ya=y1+y2; %逐点相加 yp=y1.*y2; %逐点相乘 subplot(4,1,1),stem(n,y1,'.'); line([n(1),n(end)],[0,0]); subplot(4,1,2),stem(n,y2,'.'); line([n(1),n(end)],[0,0]); subplot(4,1,3),stem(n,ya,'.'); line([n(1),n(end)],[0,0]); subplot(4,1,4),stem(n,yp,'.'); line([n(1),n(end)],[0,0]); 得到如下图所示结果: (2)序列截取操作,序列移位与周期延拓运算 1.y(n)=x(n-m)。 MATLAB实现为:y=x;ny=nx-m 2.y(n)=x((n))M,其中M表示延拓周期 MATLAB实现为:ny=nxs:nxf;y=x(mod(ny,M)+1)。 例: >> N=24;M=8;m=3; 得到如图所示结果 3.序列翻褶与序列累加运算 序列翻褶:y(n)=x(-n) MATLAB表示为:y=fliplr(x); 序列累加:y(n)=∑x(i),i∈[ns,n] MATLAB表示为:y=cumsum(x); 例: >> n=0:10; %x(n)的时间序列[0,10] >> figure(2); %新生成一个图形窗口 结果如下图所示: 4.卷积的实现 数学描述为:y(n)=h(n)*x(n) MATLAB命令为:y=conv(x,h); 例: 运行结果如下图: 注:函数conv不需要给定序列的x(n),y(n)的时间序号,也不返回y(n)=x(n)*h(n)的时间序号。所以要想正确地表示出conv的额计算结果,还需要构造x(n),y(n),h(n)的对应时间序号向量。 以下为修改后的求卷积方法: >> nx=[-5:4];x=ones(1,10); %信号序列x(n)及其时间序列nx 所得图像如下: 1.3差分方程的MATLAB求解 对常系数线性差分方程∑aky(n-k)=∑bmx(n-m)的递推求解,在MATLAB中,由以下两个函数完成: 由ys与xs求出具有常系数差分方程(B,A)的等效初始条件的输入向量。 其中ys=[y(-1),y(-2),...,y(-N)],xs=[x(-1),x(-2),...,x(-N)],B=[b0,b1,...bM],A=[a0,a1,...aN],默认a0=1,xs=0 (2)yn=filter(B,A,xn,xi) 常系数差分方程(B,A)所表示的系统在输入信号为xn和系统初始状态为xi时,系统的响应为yn。当系统初始状态xi=0时,则返回系统的零状态响应yn。 例: >> xs=0;ys=0; %系统初始状态x(-1)=0,y(-1)=0; 结果如下: 1.4连续信号的离散与重构 1.时域抽样频率与频谱混叠 首先通过一个例子来说明时域抽样频率与频谱混叠的关系 例:设连续信号xa(t)=Ae^-atsin(at)*u(t),A=444.128,a=50*2^(1/2),分别以抽样频率f=1000Hz,400Hz,200Hz进行等间隔抽样。计算并图示三种抽样频率下的抽样信号x(n)以及其幅频特性函数|Xa(jΩ)|,观察其周期以及频谱混叠程度与fs的关系。 >> fs=10000;fs1=1000;fs2=400;fs3=200; %设置4种抽样频率 //ps: axis([xmin xmax ymin ymax])作用为: 设置当前图形的坐标范围,分别为x轴的最小、最大值,y轴的最小最大值 >> xlabel('t(s)');ylabel('xa(t)');line([0,max(t)],[0,0]); 得到结果如下图: 从图中可以看出,当f≥500Hz时,|Xa(jΩ)|的值很小。所以,fs=1kHz的抽样序列x1(n)的频谱混叠很小;而fs=400Hz时,频谱混叠很大;fs=200Hz时,频谱混叠最严重。 2.由离散序列恢复模拟信号 仍然借助上一个例子来展示: A=444.128;a=50*sqrt(2)*pi;b=a; 运行结果如下图: 至于每一行命令是何意思必须看懂书上1.3.2节上的连续信号的重构,在这里就不做介绍了。。。。。。。
>> n=0:N-1; %定义域[0,23]
>> x1=(0.8).^n; %生成指数序列x1
>> x2=[(n>=0)&(n
>> xm=zeros(1,N); %生成单位脉冲序列xm
>> for k=m+1:m+M
xm(k)=x(k-m);
end; %这是一个循环,进行序列移位,将x右移m位,得到xm
>> xc=x(mod(n,M)+1); %产生x(n)的周期延拓xc
>> xcm=x(mod(n-m,M)+1); %产生x(n)移位后的周期延拓xcm
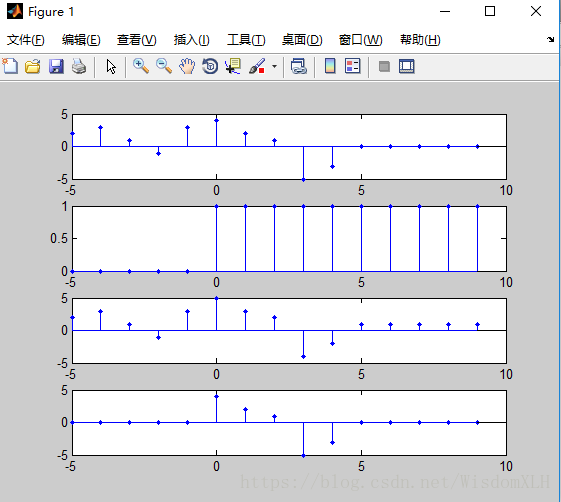
>> subplot(6,1,1),stem(n,x1,'.');
>> subplot(6,1,2),stem(n,x2,'.');
>> subplot(6,1,3),stem(n,x,'.');
>> subplot(6,1,4),stem(n,xm,'.');
>> subplot(6,1,5),stem(n,xc,'.');
>> subplot(6,1,6),stem(n,xcm,'.');
>> x=3*exp(-0.2*n); %x(n)的序列大小x(n)=3e^-0.2n
>> y=fliplr(x); %x(n)的序列翻褶
>> n1=-fliplr(n); %时间序列的翻褶(翻褶点为原点)
>> n2=fliplr(-(n-3)); %在指定位置m=3处的时间序列的翻褶
>> subplot(2,1,1);stem(n,x);
>> xlabel('n'),ylabel('x(n)');
>> subplot(2,1,2);stem(n1,y);
>> xlabel('n'),ylabel('y(n)=x(-n)');
>> s=cumsum(x); %求累加序列s(n)=∑x(i),i∈[0,n]
>> subplot(2,1,1);stem(n2,y);
>> xlabel('n'),ylabel('y(n)=x(-n+3)');
>> subplot(2,1,2);stem(n,s);
>> xlabel('n'),ylabel('s(n)');
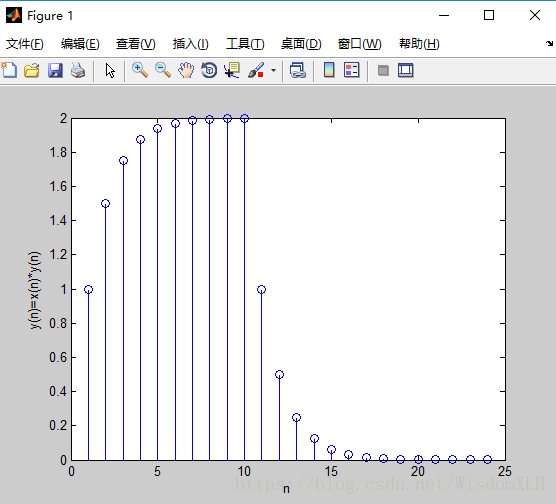
>> x=ones(1,10); %ones(M,N)函数表示产生一个M行N列的矩阵
>> n=[0:14];h=0.5.^n; %系统的单位冲激响应h(n)
>> y=conv(x,h); %卷积
>> stem(y);xlabel('n');ylabel('y(n)=x(n)*y(n)'); %生成图像
>> nh=[0:14];h=0.5.^nh; %系统的单位冲激响应序列h(n)及其时间序列nh
>> y=conv(x,h); %调用卷积函数conv求系统输出y
>> n0=nx(1)+nh(1); %求卷积序列y的起始时间位置
>> N=length(nx)+length(nh)-2; %求卷积序列y的序列长度
>> ny=n0:n0+N; %求卷积序列y的时间向量
>> subplot(2,2,1);stem(nx,n);title('x(n)');xlabel('n');yla
>> subplot(2,2,1);stem(nx,n);title('x(n)');xlabel('n');ylabel('x(n)');
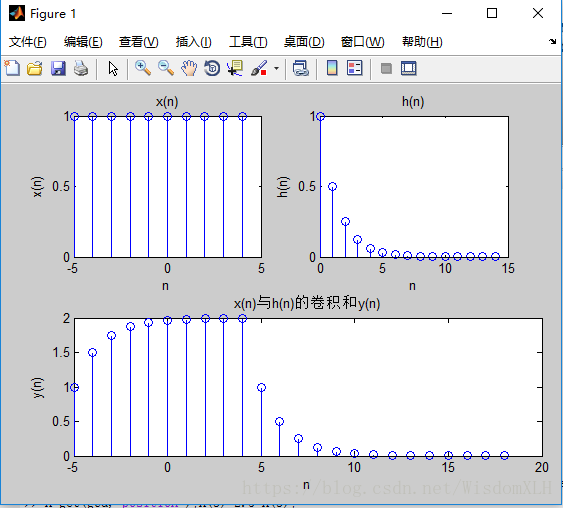
>> subplot(2,2,1);stem(nx,x);title('x(n)');xlabel('n');ylabel('x(n)');
>> subplot(2,2,2);stem(nh,h);title('h(n)');xlabel('n');ylabel('h(n)');
>> subplot(2,2,3);stem(ny,y);title('x(n)与h(n)的卷积和y(n)');xlabel('n');ylabel('y(n)');
>> h=get(gca,'position');h(3)=2.5*h(3);
>> set(gca,'position',h) %将第三个子图的横坐标范围扩为原来的2.5倍
(1)xi=filtic(B,A,ys,xs)
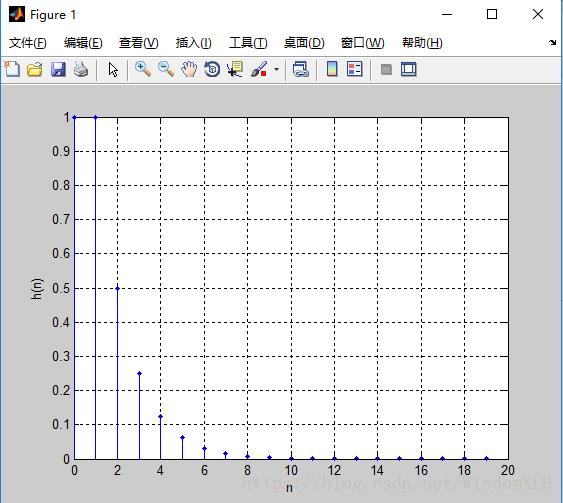
>> B=[1,0.5];A=[1,-0.5]; %差分方程为y(n)-0.5y(n-1)=x(n)+0.5x(n-1)
>> xi=filtic(B,A,ys); %求等效初始条件的输入序列xi(n)
>> xn=zeros(1,20);xn(1,1)=1; %x(n)为单位冲激序列,长度N=20
>> yn=filter(B,A,xn,xi); %调用filter解差方程,求系统输出信号
>> N=length(yn); %求输出序列y(n)的长度
>> n=0:N-1; %输出序列y(n)的时间序列
>> stem(n,yn,'.'); %制图
>> xlabel('n');ylabel('h(n)');grid;
>>t=0:1/fs:0.1; %采集信号长度为0.1s
>>A=444.128;a=50*sqrt(2)*pi;b=a; %连续信号xa(t)的参数
>> xa=exp(-a*t).*sin(b*t);
>> k=0:511;f=fs*k/512; %由wk=2Πk/512=2ΠfT求得模拟频率f
>> w=2*pi*k/512;
>> Xa=xa*exp(-j*[1:length(xa)]'*w); %近似模拟信号频谱
>> T1=1/fs1;t1=0:T1:0.1; %采集信号长度为0.1s
>> x1=A*exp(-a.*t1).*sin(b*t1); %1kHz抽样序列x1(n)
>> X1=x1*exp(-j*[1:length(x1)]'*w); %x1(n)的512点dtft
>> T2=1/fs2;t2=0:T2:0.1; %采集信号长度为0.1s
>> x2=A*exp(-a.*t2).*sin(b.*t2); %400Hz抽样序列x2(n)
>> X2=x2*exp(-j*[1:length(x2)]'*w); %x2(n)的512点dtft
>> T3=1/fs3;t3=0:T3:0.1; %采集信号长度为0.1s
>> x3=A*exp(-a.*t3).*sin(b.*t3); %200Hz抽样序列x3(n)
>> X3=x3*exp(-j*[1:length(x3)]'*w); %x3(n)的512点dtft
>> figure(1);
>> subplot(2,2,1);plot(t,xa);
>> axis([0,max(t),min(xa),max(xa)]);title('模拟信号');
>> subplot(2,2,2);plot(f,abs(Xa)/max(abs(Xa)));
>> title('模拟信号的幅度频谱');axis([0,500,0,1]);
>> xlabel('f(Hz)');ylabel('|Xa(jf)|');
>> subplot(2,2,3);stem(t1,x1,'.');
>> line([0,max(t1)],[0,0]);axis([0,max(t1),min(x1),max(x1)]);
>> title('抽样序列x1(n)(fs1=1kHz)');xlabel('n');ylabel('x1(n)');
>> f1=fs1*k/512;
>> subplot(2,2,4);plot(f1,abs(X1)/max(abs(X1)));
>> title('x1(n)的幅度谱');xlabel('f(Hz)');ylabel('|X1(jf)|');
>> figure(2);
>> subplot(2,2,1);stem(t2,x2,'.');
>> line([0,max(t2)],[0,0]);axis([0,max(t2),min(x2),max(x2)]);
>> title('抽样序列x2(n)(fs2=400Hz)');xlabel('n');ylabel('x2(n)');
>> f=fs2*k/512;
>> subplot(2,2,2);plot(f,abs(X2)/max(abs(X2)));
>> title('x2(n)的幅度谱');xlabel('f(Hz)');ylabel('|X2(jf)|');
>> subplot(2,2,3);stem(t3,x3,'.');
>> line([0,max(t3)],[0,0]);axis([0,max(t3),min(x3),max(x3)]);
>> title('抽样序列x3(n)(fs3=200Hz)');xlabel('n');ylabel('x3(n)');
>> f=fs3*k/512;
>> subplot(2,2,4);plot(f,abs(X3)/max(abs(X3)));
>> title('x3(n)的幅度谱');xlabel('f(Hz)');ylabel('|X3(jf)|');
for k=1:2
if k==1 Fs=400;
elseif k==2 Fs=1000;end
T=1/Fs;dt=T/3;
Tp=0.03;
t=0:dt:Tp;
n=0:Tp/T;
TMN=ones(length(n),1)*t-n'*T*ones(1,length(t));
x=A*exp(-a.*n*T).*sin(b*n*T);
xa=x*sinc(Fs*TMN);
subplot(2,1,k);plot(t,xa);hold on;
axis([0,max(t),min(xa)-10,max(xa)+10]);
st1=sprintf('由Fs=%d',Fs);st2='Hz的抽样序列x(n)重构的信号';
ylabel('xa(t)');
st=[st1,st2];title(st)
xo=A*exp(-a.*t).*sin(b*t);
stem(t,xo,'.');line([0,max(t)],[0,0]);
emax2=max(abs(xa-xo))
end