OpenGL入门学习
- 环境搭建
- OpenGL入门学习二
- 点直线和多边形
- 在OpenGL中指定顶点
- 开始绘制
- 例一画一个圆
- 例二画一个五角星
- 例三画出正弦函数的图形
- OpenGL入门学习三
- 关于点
- 关于直线
- 关于多边形
- OpenGL入门学习四
- RGBA颜色
- 索引颜色
- 指定清除屏幕用的颜色
- 指定着色模型
- OpenGL入门学习五
- 模型变换和视图变换
- 投影变换
- 视口变换
- 操作矩阵堆栈
- 综合举例
- OpenGL入门学习六
- 双缓冲技术
- 实现连续动画
- 关于垂直同步
- 计算帧速
- OpenGL入门学习七
- 建立光照模型
- 法线向量
- 控制光源
- 控制材质
- 选择光照模型
- 最后的准备
- 示例程序
- OpenGL入门学习八
- 分配显示列表编号
- 创建显示列表
- 调用显示列表
- 销毁显示列表
- OpenGL入门学习九
- 源因子和目标因子
- 二维图形混合举例
- 实现三维混合
环境搭建
OpenGL作为当前主流的图形API之一,它在一些场合具有比DirectX更优越的特性。
1、与C语言紧密结合。
OpenGL命令最初就是用C语言函数来进行描述的,对于学习过C语言的人来讲,OpenGL是容易理解和学习的。如果你曾经接触过TC的graphics.h,你会发现,使用OpenGL作图甚至比TC更加简单。
2、强大的可移植性。
微软的Direct3D虽然也是十分优秀的图形API,但它只用于Windows系统(现在还要加上一个XBOX游戏机)。而OpenGL不仅用于 Windows,还可以用于Unix/Linux等其它系统,它甚至在大型计算机、各种专业计算机(如:医疗用显示设备)上都有应用。并且,OpenGL 的基本命令都做到了硬件无关,甚至是平台无关。
3、高性能的图形渲染。
OpenGL是一个工业标准,它的技术紧跟时代,现今各个显卡厂家无一不对OpenGL提供强力支持,激烈的竞争中使得OpenGL性能一直领先。
总之,OpenGL是一个很NB的图形软件接口。至于究竟有多NB,去看看DOOM3和QUAKE4等专业游戏就知道了。
OpenGL官方网站(英文)
http://www.opengl.org
下面以linux为例,简介下opengl编程。这里不选择window因为不想下载庞大的winIDE工具包,而且可以看到以前在win下的示例代码几乎不用修改就可以在linux下运行。
必不可少的编译器与基本的函式库,如果系统没有安装的话,依照下面的方式安装:
$ sudo apt-get install build-essential安装OpenGL Library
$ sudo apt-get install libgl1-mesa-dev安装OpenGL Utilities
$ sudo apt-get install libglu1-mesa-devOpenGL Utilities 是一组建构于 OpenGL Library 之上的工具组,提供许多很方便的函式,使 OpenGL 更强大且更容易使用。
安装OpenGL Utility Toolkit
$ sudo apt-get install libglut-dev OpenGL Utility Toolkit 是建立在 OpenGL Utilities 上面的工具箱,除了强化了 OpenGL Utilities 的不足之外,也增加了 OpenGL 对于视窗介面支援。
注意:在这一步的时候,可能会出现以下情况,shell提示:
Reading package lists... Done
Building dependency tree
Reading state information... Done
E: Unable to locate package libglut-dev将上述
$ sudo apt-get install libglut-dev命令改成
$ sudo apt-get install freeglut3-dev即可。
测试代码test.c :
#include 编译
$ gcc -o test test.c -lGL -lGLU -lglut该程序的作用是在一个黑色的窗口中央画一个白色的矩形。下面对各行语句进行说明。
首先,需要包含头文件#include ,这是GLUT的头文件。
本来OpenGL程序一般还要包含
然后看main函数。
int main(int argc, char *argv[]),这个是带命令行参数的main函数,各位应该见过吧?没见过的同志们请多翻翻书,等弄明白了再往下看。注意main函数中的各语句,除了最后的return之外,其余全部以glut开头。这种以glut开头的函数都是GLUT工具包所提供的函数,下面对用到的几个函数进行介绍。
1、glutInit,对GLUT进行初始化,这个函数必须在其它的GLUT使用之前调用一次。其格式比较死板,一般照抄这句glutInit(&argc, argv)就可以了。
2、 glutInitDisplayMode,设置显示方式,其中GLUT_RGB表示使用RGB颜色,与之对应的还有GLUT_INDEX(表示使用索引颜色)。GLUT_SINGLE表示使用单缓冲,与之对应的还有GLUT_DOUBLE(使用双缓冲)。更多信息,请自己Google。当然以后的教程也会有一些讲解。
3、glutInitWindowPosition,这个简单,设置窗口在屏幕中的位置。
4、glutInitWindowSize,这个也简单,设置窗口的大小。
5、glutCreateWindow,根据前面设置的信息创建窗口。参数将被作为窗口的标题。注意:窗口被创建后,并不立即显示到屏幕上。需要调用glutMainLoop才能看到窗口。
6、glutDisplayFunc,设置一个函数,当需要进行画图时,这个函数就会被调用。(这个说法不够准确,但准确的说法可能初学者不太好理解,暂时这样说吧)。
7、glutMainLoop,进行一个消息循环。(这个可能初学者也不太明白,现在只需要知道这个函数可以显示窗口,并且等待窗口关闭后才会返回,这就足够了。)
在glutDisplayFunc函数中,我们设置了“当需要画图时,请调用myDisplay函数”。于是myDisplay函数就用来画图。观察myDisplay中的三个函数调用,发现它们都以gl开头。这种以gl开头的函数都是OpenGL的标准函数,下面对用到的函数进行介绍。
1、glClear,清除。GL_COLOR_BUFFER_BIT表示清除颜色,glClear函数还可以清除其它的东西,但这里不作介绍。
2、glRectf,画一个矩形。四个参数分别表示了位于对角线上的两个点的横、纵坐标。
3、glFlush,保证前面的OpenGL命令立即执行(而不是让它们在缓冲区中等待)。其作用跟fflush(stdout)类似。
OpenGL入门学习[二]
本次课程所要讲的是绘制简单的几何图形,在实际绘制之前,让我们先熟悉一些概念。
点、直线和多边形
我们知道数学(具体的说,是几何学)中有点、直线和多边形的概念,但这些概念在计算机中会有所不同。数学上的点,只有位置,没有大小。但在计算机中,无论计算精度如何提高,始终不能表示一个无穷小的点。另一方面,无论图形输出设备(例如,显示器)如何精确,始终不能输出一个无穷小的点。一般情况下,OpenGL中的点将被画成单个的像素(像素的概念,请自己搜索之~),虽然它可能足够小,但并不会是无穷小。同一像素上,OpenGL可以绘制许多坐标只有稍微不同的点,但该像素的具体颜色将取决于OpenGL的实现。当然,过度的注意细节就是钻牛角尖,我们大可不必花费过多的精力去研究“多个点如何画到同一像素上”。同样的,数学上的直线没有宽度,但OpenGL的直线则是有宽度的。同时,OpenGL的直线必须是有限长度,而不是像数学概念那样是无限的。可以认为,OpenGL的“直线”概念与数学上的“线段”接近,它可以由两个端点来确定。多边形是由多条线段首尾相连而形成的闭合区域。OpenGL规定,一个多边形必须是一个“凸多边形”(其定义为:多边形内任意两点所确定的线段都在多边形内,由此也可以推导出,凸多边形不能是空心的)。多边形可以由其边的端点(这里可称为顶点)来确定。(注意:如果使用的多边形不是凸多边形,则最后输出的效果是未定义的——OpenGL为了效率,放宽了检查,这可能导致显示错误。要避免这个错误,尽量使用三角形,因为三角形都是凸多边形)
可以想象,通过点、直线和多边形,就可以组合成各种几何图形。甚至于,你可以把一段弧看成是很多短的直线段相连,这些直线段足够短,以至于其长度小于一个像素的宽度。这样一来弧和圆也可以表示出来了。通过位于不同平面的相连的小多边形,我们还可以组成一个“曲面”。
在OpenGL中指定顶点
由以上的讨论可以知道,“点”是一切的基础。
如何指定一个点呢?OpenGL提供了一系列函数。它们都以glVertex开头,后面跟一个数字和1~2个字母。例如:
glVertex2d
glVertex2f
glVertex3f
glVertex3fv 数字表示参数的个数,2表示有两个参数,3表示三个,4表示四个(我知道有点罗嗦~)。
字母表示参数的类型:
s表示16位整数(OpenGL中将这个类型定义为GLshort),
i表示32位整数(OpenGL中将这个类型定义为GLint和GLsizei),
f表示32位浮点数(OpenGL中将这个类型定义为GLfloat和GLclampf),
d表示64位浮点数(OpenGL中将这个类型定义为GLdouble和GLclampd)。
v表示传递的几个参数将使用指针的方式,见下面的例子。
这些函数除了参数的类型和个数不同以外,功能是相同的。例如,以下五个代码段的功能是等效的:
(一)glVertex2i(1, 3);
(二)glVertex2f(1.0f, 3.0f);
(三)glVertex3f(1.0f, 3.0f, 0.0f);
(四)glVertex4f(1.0f, 3.0f, 0.0f, 1.0f);
(五)GLfloat VertexArr3[] = {1.0f, 3.0f, 0.0f};
glVertex3fv(VertexArr3);以后我们将用glVertex*来表示这一系列函数。
- 注意:OpenGL的很多函数都是采用这样的形式,一个相同的前缀再加上参数说明标记,这一点会随着学习的深入而有更多的体会。
开始绘制
假设现在我已经指定了若干顶点,那么OpenGL是如何知道我想拿这些顶点来干什么呢?是一个一个的画出来,还是连成线?或者构成一个多边形?或者做其它什么事情?
为了解决这一问题,OpenGL要求:指定顶点的命令必须包含在glBegin函数之后,glEnd函数之前(否则指定的顶点将被忽略)。并由glBegin来指明如何使用这些点。
例如我写:
glBegin(GL_POINTS);
glVertex2f(0.0f, 0.0f);
glVertex2f(0.5f, 0.0f);
glEnd(); 则这两个点将分别被画出来。如果将GL_POINTS替换成GL_LINES,则两个点将被认为是直线的两个端点,OpenGL将会画出一条直线。
我们还可以指定更多的顶点,然后画出更复杂的图形。
另一方面,glBegin支持的方式除了GL_POINTS和GL_LINES,还有GL_LINE_STRIP,GL_LINE_LOOP,GL_TRIANGLES,GL_TRIANGLE_STRIP,GL_TRIANGLE_FAN等,每种方式的大致效果见下图:
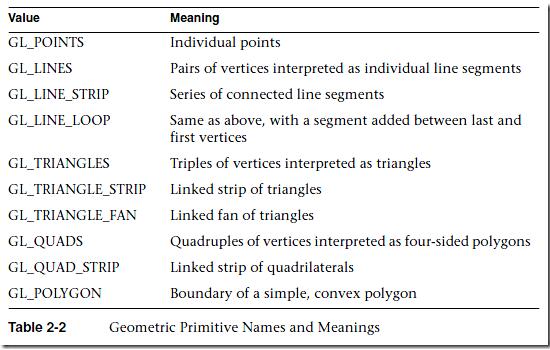
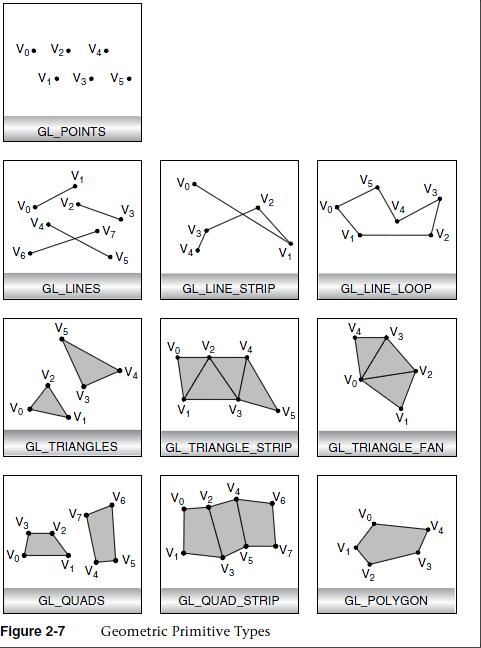
这里是对每种图形进行测试
我并不准备在glBegin的各种方式上大作文章。大家可以自己尝试改变glBegin的方式和顶点的位置,生成一些有趣的图案。
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glBegin( /* 在这里填上你所希望的模式 */ );
/* 在这里使用glVertex*系列函数 */
/* 指定你所希望的顶点位置 */
glEnd();
glFlush();
} 把这段代码改成你喜欢的样子,然后用它替换第一课中的myDisplay函数,编译后即可运行。
几个小例子:
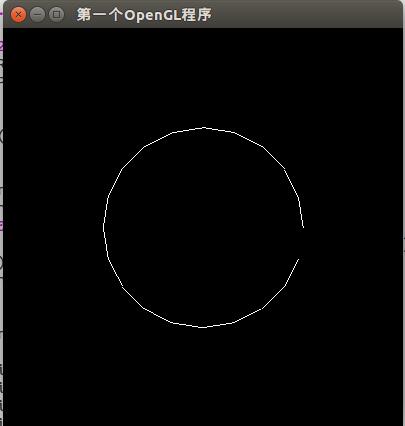
例一、画一个圆
正四边形,正五边形,正六边形,……,直到正n边形,当n越大时,这个图形就越接近圆当n大到一定程度后,人眼将无法把它跟真正的圆相区别这时我们已经成功的画出了一个“圆”
(注:画圆的方法很多,这里使用的是比较简单,但效率较低的一种)
试修改下面的const int n的值,观察当n=3,4,5,8,10,15,20,30,50等不同数值时输出的变化情况
将GL_POLYGON改为GL_LINE_LOOP、GL_POINTS等其它方式,观察输出的变化情况
#include cos(2*Pi/n*i), R*sin(2*Pi/n*i));
glEnd();
glFlush();
} 编译命令:
$ gcc -o test test.c -lGL -lGLU -lglut -lm生成图形:
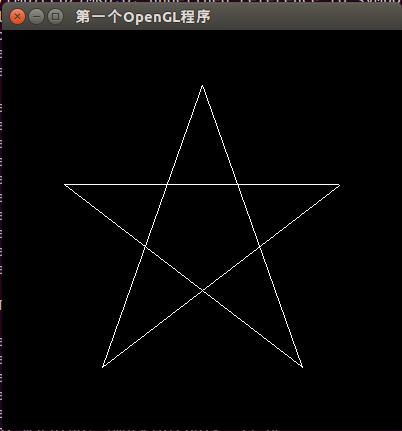
例二、画一个五角星
首先,根据余弦定理列方程,计算五角星的中心到顶点的距离a (为什么这么计算我想了很久都无法想通,高中的数学喂狗了!!TODO)
a = 1 / (2-2*cos(72*Pi/180)); 然后,根据正弦和余弦的定义,计算B的x坐标bx和y坐标by,以及C的y坐标
(假设五角星的中心在坐标原点)
bx = a * cos(18 * Pi/180);
by = a * sin(18 * Pi/180);
cy = -a * cos(18 * Pi/180);五个点的坐标就可以通过以上四个量和一些常数简单的表示出来
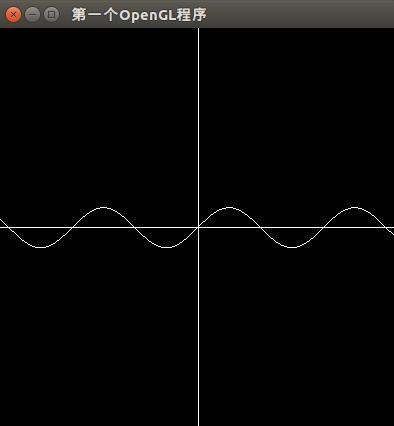
#include 例三、画出正弦函数的图形
由于OpenGL默认坐标值只能从-1到1,(可以修改,但方法留到以后讲)所以我们设置一个因子factor,把所有的坐标值等比例缩小,这样就可以画出更多个正弦周期。
试修改factor的值,观察变化情况
#include 小结
本课讲述了点、直线和多边形的概念,以及如何使用OpenGL来描述点,并使用点来描述几何图形。
大家可以发挥自己的想象,画出各种几何图形,当然,也可以用GL_LINE_STRIP把很多位置相近的点连接起来,构成函数图象。如果有兴趣,也可以去找一些图象比较美观的函数,自己动手,用OpenGL把它画出来。
OpenGL入门学习[三]
在第二课中,我们学习了如何绘制几何图形,但大家如果多写几个程序,就会发现其实还是有些郁闷之处。例如:点太小,难以看清楚;直线也太细,不舒服;或者想画虚线,但不知道方法只能用许多短直线,甚至用点组合而成。
这些问题将在本课中被解决。
下面就点、直线、多边形分别讨论。
关于点
点的大小默认为1个像素,但也可以改变之。改变的命令为glPointSize,其函数原型如下:
void glPointSize(GLfloat size);size必须大于0.0f,默认值为1.0f,单位为“像素”。
注意:对于具体的OpenGL实现,点的大小都有个限度的,如果设置的size超过最大值,则设置可能会有问题。
例子:
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glPointSize(5.0f);
glBegin(GL_POINTS);
glVertex2f(0.0f, 0.0f);
glVertex2f(0.5f, 0.5f);
glEnd();
glFlush();
}关于直线
(1)直线可以指定宽度:
void glLineWidth(GLfloat width);其用法跟glPointSize类似。
(2)画虚线。
首先,使用glEnable(GL_LINE_STIPPLE);来启动虚线模式(使用glDisable(GL_LINE_STIPPLE)可以关闭之)。
然后,使用glLineStipple来设置虚线的样式。
void glLineStipple(GLint factor, GLushort pattern); pattern是由1和0组成的长度为16的序列,从最低位开始看,如果为1,则直线上接下来应该画的factor个点将被画为实的;如果为0,则直线上接下来应该画的factor个点将被画为虚的。
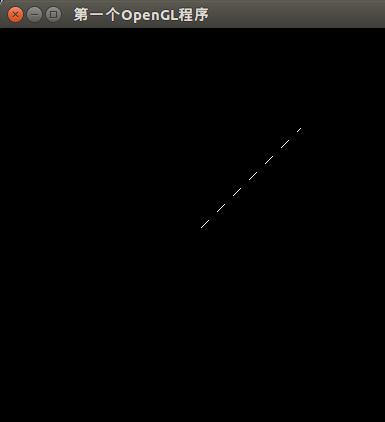
示例代码:
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glEnable(GL_LINE_STIPPLE);
glLineStipple(2, 0x0F0F);
glLineWidth(10.0f);
glBegin(GL_LINES);
glVertex2f(0.0f, 0.0f);
glVertex2f(0.5f, 0.5f);
glEnd();
glFlush();
}关于这个这里介绍的还不是很详细,可以看博文:opengl 直线的线型(各种虚线)
关于多边形
多边形的内容较多,我们将讲述以下四个方面。
(1)多边形的两面以及绘制方式。
虽然我们目前还没有真正的使用三维坐标来画图,但是建立一些三维的概念还是必要的。
从三维的角度来看,一个多边形具有两个面。每一个面都可以设置不同的绘制方式:填充、只绘制边缘轮廓线、只绘制顶点,其中“填充”是默认的方式。可以为两个面分别设置不同的方式。
glPolygonMode(GL_FRONT, GL_FILL); // 设置正面为填充方式
glPolygonMode(GL_BACK, GL_LINE); // 设置反面为边缘绘制方式
glPolygonMode(GL_FRONT_AND_BACK, GL_POINT); // 设置两面均为顶点绘制方式(2)反转
一般约定为“顶点以逆时针顺序出现在屏幕上的面”为“正面”,另一个面即成为“反面”。生活中常见的物体表面,通常都可以用这样的“正面”和“反面”,“合理的”被表现出来(请找一个比较透明的矿泉水瓶子,在正对你的一面沿逆时针画一个圆,并标明画的方向,然后将背面转为正面,画一个类似的圆,体会一下“正面”和“反面”。你会发现正对你的方向,瓶的外侧是正面,而背对你的方向,瓶的内侧才是正面。正对你的内侧和背对你的外侧则是反面。这样一来,同样属于“瓶的外侧”这个表面,但某些地方算是正面,某些地方却算是反面了)。但也有一些表面比较特殊。例如“麦比乌斯带”(请自己Google一下),可以全部使用“正面”或全部使用“背面”来表示。
可以通过glFrontFace函数来交换“正面”和“反面”的概念。
glFrontFace(GL_CCW); // 设置CCW方向为“正面”,CCW即CounterClockWise,逆时针
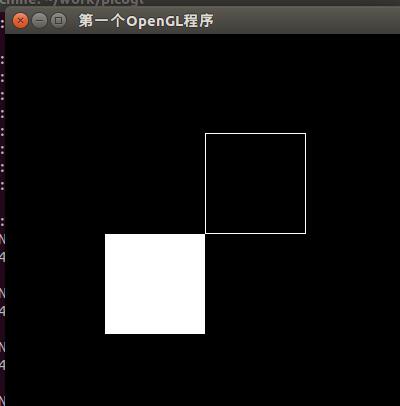
glFrontFace(GL_CW); // 设置CW方向为“正面”,CW即ClockWise,顺时针下面是一个示例程序,请用它替换第一课中的myDisplay函数,并将glFrontFace(GL_CCW)修改为glFrontFace(GL_CW),并观察结果的变化。
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glPolygonMode(GL_FRONT, GL_FILL); // 设置正面为填充模式
glPolygonMode(GL_BACK, GL_LINE); // 设置反面为线形模式
glFrontFace(GL_CCW); // 设置逆时针方向为正面
glBegin(GL_POLYGON); // 按逆时针绘制一个正方形,在左下方
glVertex2f(-0.5f, -0.5f);
glVertex2f(0.0f, -0.5f);
glVertex2f(0.0f, 0.0f);
glVertex2f(-0.5f, 0.0f);
glEnd();
glBegin(GL_POLYGON); // 按顺时针绘制一个正方形,在右上方
glVertex2f(0.0f, 0.0f);
glVertex2f(0.0f, 0.5f);
glVertex2f(0.5f, 0.5f);
glVertex2f(0.5f, 0.0f);
glEnd();
glFlush();
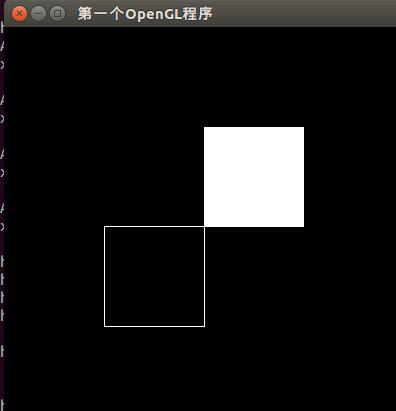
}将glFrontFace(GL_CCW)修改为glFrontFace(GL_CW)之后运行结果:
(3)剔除多边形表面
在三维空间中,一个多边形虽然有两个面,但我们无法看见背面的那些多边形,而一些多边形虽然是正面的,但被其他多边形所遮挡。如果将无法看见的多边形和可见的多边形同等对待,无疑会降低我们处理图形的效率。在这种时候,可以将不必要的面剔除。
首先,使用glEnable(GL_CULL_FACE);来启动剔除功能(使用glDisable(GL_CULL_FACE)可以关闭之)
然后,使用glCullFace来进行剔除。
glCullFace的参数可以是GL_FRONT,GL_BACK或者GL_FRONT_AND_BACK,分别表示剔除正面、剔除反面、剔除正反两面的多边形。
注意:剔除功能只影响多边形,而对点和直线无影响。例如,使用glCullFace(GL_FRONT_AND_BACK)后,所有的多边形都将被剔除,所以看见的就只有点和直线。
(4)镂空多边形
直线可以被画成虚线,而多边形则可以进行镂空。
首先,使用glEnable(GL_POLYGON_STIPPLE);来启动镂空模式(使用glDisable(GL_POLYGON_STIPPLE)可以关闭之)。
然后,使用glPolygonStipple来设置镂空的样式。
void glPolygonStipple(const GLubyte *mask);其中的参数mask指向一个长度为128字节的空间,它表示了一个32*32的矩形应该如何镂空。其中:第一个字节表示了最左下方的从左到右(也可以是从右到左,这个可以修改)8个像素是否镂空(1表示不镂空,显示该像素;0表示镂空,显示其后面的颜色),最后一个字节表示了最右上方的8个像素是否镂空。
但是,如果我们直接定义这个mask数组,像这样:
static GLubyte Mask[128] =
{
0x00, 0x00, 0x00, 0x00, // 这是最下面的一行
0x00, 0x00, 0x00, 0x00,
0x03, 0x80, 0x01, 0xC0, // 麻
0x06, 0xC0, 0x03, 0x60, // 烦
0x04, 0x60, 0x06, 0x20, // 的
0x04, 0x30, 0x0C, 0x20, // 初
0x04, 0x18, 0x18, 0x20, // 始
0x04, 0x0C, 0x30, 0x20, // 化
0x04, 0x06, 0x60, 0x20, // ,
0x44, 0x03, 0xC0, 0x22, // 不
0x44, 0x01, 0x80, 0x22, // 建
0x44, 0x01, 0x80, 0x22, // 议
0x44, 0x01, 0x80, 0x22, // 使
0x44, 0x01, 0x80, 0x22, // 用
0x44, 0x01, 0x80, 0x22,
0x44, 0x01, 0x80, 0x22,
0x66, 0x01, 0x80, 0x66,
0x33, 0x01, 0x80, 0xCC,
0x19, 0x81, 0x81, 0x98,
0x0C, 0xC1, 0x83, 0x30,
0x07, 0xE1, 0x87, 0xE0,
0x03, 0x3F, 0xFC, 0xC0,
0x03, 0x31, 0x8C, 0xC0,
0x03, 0x3F, 0xFC, 0xC0,
0x06, 0x64, 0x26, 0x60,
0x0C, 0xCC, 0x33, 0x30,
0x18, 0xCC, 0x33, 0x18,
0x10, 0xC4, 0x23, 0x08,
0x10, 0x63, 0xC6, 0x08,
0x10, 0x30, 0x0C, 0x08,
0x10, 0x18, 0x18, 0x08,
0x10, 0x00, 0x00, 0x08 // 这是最上面的一行
};这样一堆数据非常缺乏直观性,我们需要很费劲的去分析,才会发现它表示的竟然是一只苍蝇。如果将这样的数据保存成图片,并用专门的工具进行编辑,显然会方便很多。下面介绍如何做到这一点。
首先,用Windows自带的画笔程序新建一副图片,取名为mask.bmp,注意保存时,应该选择“单色位图”。在“图象”->“属性”对话框中,设置图片的高度和宽度均为32。
用放大镜观察图片,并编辑之。黑色对应二进制零(镂空),白色对应二进制一(不镂空),编辑完毕后保存。
然后,就可以使用以下代码来获得这个Mask数组了。
static GLubyte Mask[128];
FILE *fp;
fp = fopen("mask.bmp", "rb");
if( !fp )
exit(0);
// 移动文件指针到这个位置,使得再读sizeof(Mask)个字节就会遇到文件结束
// 注意-(int)sizeof(Mask)虽然不是什么好的写法,但这里它确实是正确有效的
// 如果直接写-sizeof(Mask)的话,因为sizeof取得的是一个无符号数,取负号会有问题
if( fseek(fp, -(int)sizeof(Mask), SEEK_END) )
exit(0);
// 读取sizeof(Mask)个字节到Mask
if( !fread(Mask, sizeof(Mask), 1, fp) )
exit(0);
fclose(fp); 好的,现在请自己编辑一个图片作为mask,并用上述方法取得Mask数组,运行后观察效果。
说明:绘制虚线时可以设置factor因子,但多边形的镂空无法设置factor因子。请用鼠标改变窗口的大小,观察镂空效果的变化情况。
#include 小结
本课学习了绘制几何图形的一些细节。
点可以设置大小。
直线可以设置宽度;可以将直线画成虚线。
多边形的两个面的绘制方法可以分别设置;在三维空间中,不可见的多边形可以被剔除;可以将填充多边形绘制成镂空的样式。
了解这些细节会使我们在一些图象绘制中更加得心应手。
另外,把一些数据写到程序之外的文件中,并用专门的工具编辑之,有时可以显得更方便。
OpenGL入门学习[四]
本次学习的是颜色的选择。终于要走出黑白的世界了~~
OpenGL支持两种颜色模式:一种是RGBA,一种是颜色索引模式。
无论哪种颜色模式,计算机都必须为每一个像素保存一些数据。不同的是,RGBA模式中,数据直接就代表了颜色;而颜色索引模式中,数据代表的是一个索引,要得到真正的颜色,还必须去查索引表。
RGBA颜色
RGBA模式中,每一个像素会保存以下数据:R值(红色分量)、G值(绿色分量)、B值(蓝色分量)和A值(alpha分量)。其中红、绿、蓝三种颜色相组合,就可以得到我们所需要的各种颜色,而alpha不直接影响颜色,它将留待以后介绍。
在RGBA模式下选择颜色是十分简单的事情,只需要一个函数就可以搞定。
glColor*系列函数可以用于设置颜色,其中三个参数的版本可以指定R、G、B的值,而A值采用默认;四个参数的版本可以分别指定R、G、B、A的值。
例如:
void glColor3f(GLfloat red, GLfloat green, GLfloat blue);
void glColor4f(GLfloat red, GLfloat green, GLfloat blue, GLfloat alpha);(还记得吗?3f表示有三个浮点参数~请看第二课中关于glVertex*函数的叙述。)
将浮点数作为参数,其中0.0表示不使用该种颜色,而1.0表示将该种颜色用到最多。例如:
glColor3f(1.0f, 0.0f, 0.0f); 表示不使用绿、蓝色,而将红色使用最多,于是得到最纯净的红色。
glColor3f(0.0f, 1.0f, 1.0f); 表示使用绿、蓝色到最多,而不使用红色。混合的效果就是浅蓝色。
glColor3f(0.5f, 0.5f, 0.5f); 表示各种颜色使用一半,效果为灰色。
注意:浮点数可以精确到小数点后若干位,这并不表示计算机就可以显示如此多种颜色。实际上,计算机可以显示的颜色种数将由硬件决定。如果OpenGL找不到精确的颜色,会进行类似“四舍五入”的处理。
大家可以通过改变下面代码中glColor3f的参数值,绘制不同颜色的矩形。
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(0.0f, 1.0f, 1.0f);
glRectf(-0.5f, -0.5f, 0.5f, 0.5f);
glFlush();
}注意:glColor系列函数,在参数类型不同时,表示“最大”颜色的值也不同。
采用f和d做后缀的函数,以1.0表示最大的使用。
采用b做后缀的函数,以127表示最大的使用。
采用ub做后缀的函数,以255表示最大的使用。
采用s做后缀的函数,以32767表示最大的使用。
采用us做后缀的函数,以65535表示最大的使用。
这些规则看似麻烦,但熟悉后实际使用中不会有什么障碍。
索引颜色
在索引颜色模式中,OpenGL需要一个颜色表。这个表就相当于画家的调色板:虽然可以调出很多种颜色,但同时存在于调色板上的颜色种数将不会超过调色板的格数。试将颜色表的每一项想象成调色板上的一个格子:它保存了一种颜色。
在使用索引颜色模式画图时,我说“我把第i种颜色设置为某某”,其实就相当于将调色板的第i格调为某某颜色。“我需要第k种颜色来画图”,那么就用画笔去蘸一下第k格调色板。
颜色表的大小是很有限的,一般在256~4096之间,且总是2的整数次幂。在使用索引颜色方式进行绘图时,总是先设置颜色表,然后选择颜色。
选择颜色
使用glIndex*系列函数可以在颜色表中选择颜色。其中最常用的可能是glIndexi,它的参数是一个整形。
void glIndexi(GLint c);是的,这的确很简单。
设置颜色表
OpenGL 并没有直接提供设置颜色表的方法,因此设置颜色表需要使用操作系统的支持。原文的例子是在windows下设置颜色表,这里略过。
指定清除屏幕用的颜色
我们写:glClear(GL_COLOR_BUFFER_BIT);意思是把屏幕上的颜色清空。
但实际上什么才叫“空”呢?在宇宙中,黑色代表了“空”;在一张白纸上,白色代表了“空”;在信封上,信封的颜色才是“空”。
OpenGL用下面的函数来定义清楚屏幕后屏幕所拥有的颜色。
在RGB模式下,使用glClearColor来指定“空”的颜色,它需要四个参数,其参数的意义跟glColor4f相似。
在索引颜色模式下,使用glClearIndex来指定“空”的颜色所在的索引,它需要一个参数,其意义跟glIndexi相似。
void myDisplay(void)
{
glClearColor(1.0f, 0.0f, 0.0f, 0.0f);
glClear(GL_COLOR_BUFFER_BIT);
glFlush();
}呵,这个还真简单~
指定着色模型
OpenGL允许为同一多边形的不同顶点指定不同的颜色。例如:
#include 显示效果:

在默认情况下,OpenGL会计算两点顶点之间的其它点,并为它们填上“合适”的颜色,使相邻的点的颜色值都比较接近。如果使用的是RGB模式,看起来就具有渐变的效果。如果是使用颜色索引模式,则其相邻点的索引值是接近的—如果将颜色表中接近的项设置成接近的颜色,则看起来也是渐变的效果。但如果颜色表中接近的项颜色却差距很大,则看起来可能是很奇怪的效果。
使用glShadeModel函数可以关闭这种计算,如果顶点的颜色不同,则将顶点之间的其它点全部设置为与某一个点相同。(直线以后指定的点的颜色为准,而多边形将以任意顶点的颜色为准,由实现决定。)为了避免这个不确定性,尽量在多边形中使用同一种颜色。
glShadeModel的使用方法:
glShadeModel(GL_SMOOTH); // 平滑方式,这也是默认方式
glShadeModel(GL_FLAT); // 单色方式小结:
本课学习了如何设置颜色。其中RGB颜色方式是目前PC机上的常用方式。
可以设置glClear清除后屏幕所剩的颜色。
可以设置颜色填充方式:平滑方式或单色方式。
OpenGL入门学习[五]
今天要讲的是三维变换的内容,课程比较枯燥。主要是因为很多函数在单独使用时都不好描述其效果,我只好在最后举一个比较综合的例子。希望大家能一口气看到底了。只看一次可能不够,如果感觉到迷糊,不妨多看两遍。有疑问可以在下面跟帖提出。
我也使用了若干图形,希望可以帮助理解。
在前面绘制几何图形的时候,大家是否觉得我们绘图的范围太狭隘了呢?坐标只能从-1到1,还只能是X轴向右,Y轴向上,Z轴垂直屏幕。这些限制给我们的绘图带来了很多不便。
我们生活在一个三维的世界——如果要观察一个物体,我们可以:
1、从不同的位置去观察它。(视图变换)
2、移动或者旋转它,当然了,如果它只是计算机里面的物体,我们还可以放大或缩小它。(模型变换)
3、如果把物体画下来,我们可以选择:是否需要一种“近大远小”的透视效果。另外,我们可能只希望看到物体的一部分,而不是全部(剪裁)。(投影变换)
4、我们可能希望把整个看到的图形画下来,但它只占据纸张的一部分,而不是全部。(视口变换)
这些,都可以在OpenGL中实现。
OpenGL变换实际上是通过矩阵乘法来实现。无论是移动、旋转还是缩放大小,都是通过在当前矩阵的基础上乘以一个新的矩阵来达到目的。关于矩阵的知识,这里不详细介绍,有兴趣的朋友可以看看线性代数(PS 当年线性代数本学渣就逃课弄了个专门解线性代数题的程序,居然让我弄成了,整本书几乎所有的向量,矩阵,行列式都能解答,成就感啊!)。
OpenGL可以在最底层直接操作矩阵,不过作为初学,这样做的意义并不大。这里就不做介绍了。
模型变换和视图变换
从“相对移动”的观点来看,改变观察点的位置与方向和改变物体本身的位置与方向具有等效性。在OpenGL中,实现这两种功能甚至使用的是同样的函数。
由于模型和视图的变换都通过矩阵运算来实现,在进行变换前,应先设置当前操作的矩阵为“模型视图矩阵”。设置的方法是以GL_MODELVIEW为参数调用glMatrixMode函数,像这样:
glMatrixMode(GL_MODELVIEW);通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。这也只需要一行代码:
glLoadIdentity();然后,就可以进行 模型变换和视图变换了。进行模型和视图变换,主要涉及到三个函数:
glTranslate*,把当前矩阵和一个表示移动物体的矩阵相乘。三个参数分别表示了在三个坐标上的位移值。
glRotate*,把当前矩阵和一个表示旋转物体的矩阵相乘。物体将绕着(0,0,0)到(x,y,z)的直线以逆时针旋转,参数angle表示旋转的角度。
glScale*,把当前矩阵和一个表示缩放物体的矩阵相乘。x,y,z分别表示在该方向上的缩放比例。
注意我都是说“与XX相乘”,而不是直接说“这个函数就是旋转”或者“这个函数就是移动”,这是有原因的,马上就会讲到。
假设当前矩阵为单位矩阵,然后先乘以一个表示旋转的矩阵R,再乘以一个表示移动的矩阵T,最后得到的矩阵再乘上每一个顶点的坐标矩阵v。所以,经过变换得到的顶点坐标就是((RT)v)。由于矩阵乘法的结合率,((RT)v) = (R(Tv)),换句话说,实际上是先进行移动,然后进行旋转。即:实际变换的顺序与代码中写的顺序是相反的。由于“先移动后旋转”和“先旋转后移动”得到的结果很可能不同,初学的时候需要特别注意这一点。
OpenGL之所以这样设计,是为了得到更高的效率。但在绘制复杂的三维图形时,如果每次都去考虑如何把变换倒过来,也是很痛苦的事情。这里介绍另一种思路,可以让代码看起来更自然(写出的代码其实完全一样,只是考虑问题时用的方法不同了)。
让我们想象,坐标并不是固定不变的。旋转的时候,坐标系统随着物体旋转。移动的时候,坐标系统随着物体移动。如此一来,就不需要考虑代码的顺序反转的问题了。
以上都是针对改变物体的位置和方向来介绍的。如果要改变观察点的位置,除了配合使用glRotate*和glTranslate*函数以外,还可以使用这个函数:gluLookAt。它的参数比较多,前三个参数表示了观察点的位置,中间三个参数表示了观察目标的位置,最后三个参数代表从(0,0,0)到 (x,y,z)的直线,它表示了观察者认为的“上”方向。
投影变换
投影变换就是定义一个可视空间,可视空间以外的物体不会被绘制到屏幕上。(注意,从现在起,坐标可以不再是-1.0到1.0了!)
OpenGL支持两种类型的投影变换,即透视投影和正投影。投影也是使用矩阵来实现的。如果需要操作投影矩阵,需要以GL_PROJECTION为参数调用glMatrixMode函数。
glMatrixMode(GL_PROJECTION);通常,我们需要在进行变换前把当前矩阵设置为单位矩阵。
glLoadIdentity(); 透视投影所产生的结果类似于照片,有近大远小的效果,比如在火车头内向前照一个铁轨的照片,两条铁轨似乎在远处相交了。
使用glFrustum函数可以将当前的可视空间设置为透视投影空间。也可以使用更常用的gluPerspective函数。
正投影相当于在无限远处观察得到的结果,它只是一种理想状态。但对于计算机来说,使用正投影有可能获得更好的运行速度。使用glOrtho函数可以将当前的可视空间设置为正投影空间。
如果绘制的图形空间本身就是二维的,可以使用gluOrtho2D。他的使用类似于glOrgho。
视口变换
当一切工作已经就绪,只需要把像素绘制到屏幕上了。这时候还剩最后一个问题:应该把像素绘制到窗口的哪个区域呢?通常情况下,默认是完整的填充整个窗口,但我们完全可以只填充一半。(即:把整个图象填充到一半的窗口内)
使用glViewport来定义视口。其中前两个参数定义了视口的左下脚(0,0表示最左下方),后两个参数分别是宽度和高度。
操作矩阵堆栈
鉴于是入门教程,先简单介绍一下堆栈。你可以把堆栈想象成一叠盘子。开始的时候一个盘子也没有,你可以一个一个往上放,也可以一个一个取下来。每次取下的,都是最后一次被放上去的盘子。通常,在计算机实现堆栈时,堆栈的容量是有限的,如果盘子过多,就会出错。当然,如果没有盘子了,再要求取一个盘子,也会出错。(最基本的数据结构了,就是一个先进后出)
我们在进行矩阵操作时,有可能需要先保存某个矩阵,过一段时间再恢复它。当我们需要保存时,调用glPushMatrix函数,它相当于把矩阵(相当于盘子)放到堆栈上。当需要恢复最近一次的保存时,调用glPopMatrix函数,它相当于把矩阵从堆栈上取下。OpenGL规定堆栈的容量至少可以容纳32个矩阵,某些OpenGL实现中,堆栈的容量实际上超过了32个。因此不必过于担心矩阵的容量问题。
通常,用这种先保存后恢复的措施,比先变换再逆变换要更方便,更快速。
注意:模型视图矩阵和投影矩阵都有相应的堆栈。使用glMatrixMode来指定当前操作的究竟是模型视图矩阵还是投影矩阵。
综合举例
好了,视图变换的入门知识差不多就讲完了。但我们不能就这样结束。因为本次课程的内容实在过于枯燥,如果分别举例,可能效果不佳。我只好综合的讲一个例子,算是给大家一个参考。至于实际的掌握,还要靠大家自己花功夫。闲话少说,现在进入正题。
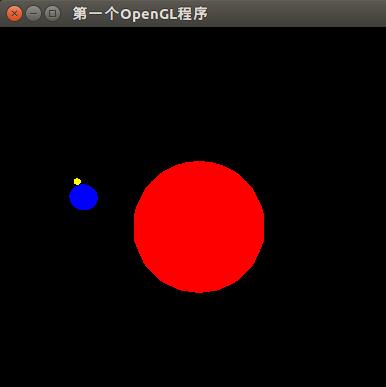
我们要制作的是一个三维场景,包括了太阳、地球和月亮。假定一年有12个月,每个月30天。每年,地球绕着太阳转一圈。每个月,月亮围着地球转一圈。即一年有360天。
现在给出日期的编号(0~359),要求绘制出太阳、地球、月亮的相对位置示意图。(这是为了编程方便才这样设计的。如果需要制作更现实的情况,那也只是一些数值处理而已,与OpenGL关系不大)
首先,让我们认定这三个天体都是球形,且他们的运动轨迹处于同一水平面,建立以下坐标系:太阳的中心为原点,天体轨迹所在的平面表示了X轴与Y轴决定的平面,且每年第一天,地球在X轴正方向上,月亮在地球的正X轴方向。
下一步是确立可视空间。注意:太阳的半径要比太阳到地球的距离短得多。如果我们直接使用天文观测得到的长度比例,则当整个窗口表示地球轨道大小时,太阳的大小将被忽略。因此,我们只能成倍的放大几个天体的半径,以适应我们观察的需要。(百度一下,得到太阳、地球、月亮的大致半径分别是:696000km,6378km,1738km。地球到太阳的距离约为1.5亿km=150000000km,月亮到地球的距离约为380000km。)
让我们假想一些数据,将三个天体的半径分别“修改”为:69600000(放大100倍),15945000(放大2500倍),4345000(放大2500倍)。将地球到月亮的距离“修改”为38000000(放大100倍)。地球到太阳的距离保持不变。
为了让地球和月亮在离我们很近时,我们仍然不需要变换观察点和观察方向就可以观察它们,我们把观察点放在这个位置:(0, -200000000, 0) ——因为地球轨道半径为150000000,咱们就凑个整,取-200000000就可以了。观察目标设置为原点(即太阳中心),选择Z轴正方向作为 “上”方。当然我们还可以把观察点往“上”方移动一些,得到(0, -200000000, 200000000),这样可以得到45度角的俯视效果。
为了得到透视效果,我们使用gluPerspective来设置可视空间。假定可视角为60度(如果调试时发现该角度不合适,可修改之。我在最后选择的数值是75。)高宽比为1.0。最近可视距离为1.0,最远可视距离为200000000*2=400000000。即:gluPerspective (60, 1, 1, 400000000);现在我们来看看如何绘制这三个天体。
为了简单起见,我们把三个天体都想象成规则的球体。而我们所使用的glut实用工具中,正好就有一个绘制球体的现成函数:glutSolidSphere,这个函数在“原点”绘制出一个球体。由于坐标是可以通过glTranslate*和glRotate*两个函数进行随意变换的,所以我们就可以在任意位置绘制球体了。函数有三个参数:第一个参数表示球体的半径,后两个参数代表了“面”的数目,简单点说就是球体的精确程度,数值越大越精确,当然代价就是速度越缓慢。这里我们只是简单的设置后两个参数为20。
太阳在坐标原点,所以不需要经过任何变换,直接绘制就可以了。
地球则要复杂一点,需要变换坐标。由于今年已经经过的天数已知为day,则地球转过的角度为day/一年的天数*360度。前面已经假定每年都是360天,因此地球转过的角度恰好为day。所以可以通过下面的代码来解决:
glRotatef(day, 0, 0, -1);
/* 注意地球公转是“自西向东”的,因此是饶着Z轴负方向进行逆时针旋转 */
glTranslatef(地球轨道半径, 0, 0);
glutSolidSphere(地球半径, 20, 20);月亮是最复杂的。因为它不仅要绕地球转,还要随着地球绕太阳转。但如果我们选择地球作为参考,则月亮进行的运动就是一个简单的圆周运动了。如果我们先绘制地球,再绘制月亮,则只需要进行与地球类似的变换:
glRotatef(月亮旋转的角度, 0, 0, -1);
glTranslatef(月亮轨道半径, 0, 0);
glutSolidSphere(月亮半径, 20, 20); 但这个“月亮旋转的角度”,并不能简单的理解为day/一个月的天数30*360度。因为我们在绘制地球时,这个坐标已经是旋转过的。现在的旋转是在以前的基础上进行旋转,因此还需要处理这个“差值”。我们可以写成:day/30*360 - day,即减去原来已经转过的角度。这只是一种简单的处理,当然也可以在绘制地球前用glPushMatrix保存矩阵,绘制地球后用glPopMatrix恢复矩阵。再设计一个跟地球位置无关的月亮位置公式,来绘制月亮。通常后一种方法比前一种要好,因为浮点的运算是不精确的,即是说我们计算地球本身的位置就是不精确的。拿这个不精确的数去计算月亮的位置,会导致 “不精确”的成分累积,过多的“不精确”会造成错误。我们这个小程序没有去考虑这个,但并不是说这个问题不重要。
还有一个需要注意的细节: OpenGL把三维坐标中的物体绘制到二维屏幕,绘制的顺序是按照代码的顺序来进行的。因此后绘制的物体会遮住先绘制的物体,即使后绘制的物体在先绘制的物体的“后面”也是如此。使用深度测试可以解决这一问题。使用的方法是:
1、以GL_DEPTH_TEST为参数调用glEnable函数,启动深度测试。
2、在必要时(通常是每次绘制画面开始时),清空深度缓冲,即:glClear(GL_DEPTH_BUFFER_BIT);其中,glClear (GL_COLOR_BUFFER_BIT)与glClear(GL_DEPTH_BUFFER_BIT)可以合并写为:glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT); 且后者的运行速度可能比前者快。
到此为止,我们终于可以得到整个“太阳,地球和月亮”系统的完整代码。
// 太阳、地球和月亮
// 假设每个月都是30天
// 一年12个月,共是360天
static int day = 200; // day的变化:从0到359
void myDisplay(void)
{
glEnable(GL_DEPTH_TEST);
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
gluPerspective(75, 1, 1, 400000000);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
gluLookAt(0, -200000000, 200000000, 0, 0, 0, 0, 0, 1);
// 绘制红色的“太阳”
glColor3f(1.0f, 0.0f, 0.0f);
glutSolidSphere(69600000, 20, 20);
// 绘制蓝色的“地球”
glColor3f(0.0f, 0.0f, 1.0f);
glRotatef(day/360.0*360.0, 0.0f, 0.0f, -1.0f);
glTranslatef(150000000, 0.0f, 0.0f);
glutSolidSphere(15945000, 20, 20);
// 绘制黄色的“月亮”
glColor3f(1.0f, 1.0f, 0.0f);
glRotatef(day/30.0*360.0 - day/360.0*360.0, 0.0f, 0.0f, -1.0f);
glTranslatef(38000000, 0.0f, 0.0f);
glutSolidSphere(4345000, 20, 20);
glFlush();
}小结:本课开始,我们正式进入了三维的OpenGL世界。
OpenGL通过矩阵变换来把三维物体转变为二维图象,进而在屏幕上显示出来。为了指定当前操作的是何种矩阵,我们使用了函数glMatrixMode。
我们可以移动、旋转观察点或者移动、旋转物体,使用的函数是glTranslate*和glRotate*。
我们可以缩放物体,使用的函数是glScale*。
我们可以定义可视空间,这个空间可以是“正投影”的(使用glOrtho或gluOrtho2D),也可以是“透视投影”的(使用glFrustum或gluPerspective)。
我们可以定义绘制到窗口的范围,使用的函数是glViewport。
矩阵有自己的“堆栈”,方便进行保存和恢复。这在绘制复杂图形时很有帮助。使用的函数是glPushMatrix和glPopMatrix。
好了,艰苦的一课终于完毕。我知道,本课的内容十分枯燥,就连最后的例子也是。但我也没有更好的办法了,希望大家能坚持过去。不必担心,熟悉本课内容后,以后的一段时间内,都会是比较轻松愉快的了。
OpenGL入门学习[六]
今天要讲的是动画制作——可能是各位都很喜欢的。除了讲授知识外,我们还会让昨天那个“太阳、地球和月亮”天体图画动起来。缓和一下枯燥的气氛。
本次课程,我们将进入激动人心的计算机动画世界。
想必大家都知道电影和动画的工作原理吧?是的,快速的把看似连续的画面一幅幅的呈现在人们面前。一旦每秒钟呈现的画面超过24幅,人们就会错以为它是连续的。
我们通常观看的电视,每秒播放25或30幅画面。但对于计算机来说,它可以播放更多的画面,以达到更平滑的效果。如果速度过慢,画面不够平滑。如果速度过快,则人眼未必就能反应得过来。对于一个正常人来说,每秒60~120幅图画是比较合适的。具体的数值因人而异。
假设某动画一共有n幅画面,则它的工作步骤就是:
显示第1幅画面,然后等待一小段时间,直到下一个1/24秒
显示第2幅画面,然后等待一小段时间,直到下一个1/24秒
……
显示第n幅画面,然后等待一小段时间,直到下一个1/24秒
结束
如果用C语言伪代码来描述这一过程,就是:
for(i=0; ii)
{
DrawScene(i);
Wait();
} 双缓冲技术
在计算机上的动画与实际的动画有些不同:实际的动画都是先画好了,播放的时候直接拿出来显示就行。计算机动画则是画一张,就拿出来一张,再画下一张,再拿出来。如果所需要绘制的图形很简单,那么这样也没什么问题。但一旦图形比较复杂,绘制需要的时间较长,问题就会变得突出。
让我们把计算机想象成一个画图比较快的人,假如他直接在屏幕上画图,而图形比较复杂,则有可能在他只画了某幅图的一半的时候就被观众看到。而后面虽然他把画补全了,但观众的眼睛却又没有反应过来,还停留在原来那个残缺的画面上。也就是说,有时候观众看到完整的图象,有时却又只看到残缺的图象,这样就造成了屏幕的闪烁。
如何解决这一问题呢?我们设想有两块画板,画图的人在旁边画,画好以后把他手里的画板与挂在屏幕上的画板相交换。这样以来,观众就不会看到残缺的画了。这一技术被应用到计算机图形中,称为双缓冲技术。即:在存储器(很有可能是显存)中开辟两块区域,一块作为发送到显示器的数据,一块作为绘画的区域,在适当的时候交换它们。由于交换两块内存区域实际上只需要交换两个指针,这一方法效率非常高,所以被广泛的采用。
注意:虽然绝大多数平台都支持双缓冲技术,但这一技术并不是OpenGL标准中的内容。OpenGL为了保证更好的可移植性,允许在实现时不使用双缓冲技术。当然,我们常用的PC都是支持双缓冲技术的。
要启动双缓冲功能,最简单的办法就是使用GLUT工具包。我们以前在main函数里面写:
glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE); 其中GLUT_SINGLE表示单缓冲,如果改成GLUT_DOUBLE就是双缓冲了。
当然还有需要更改的地方——每次绘制完成时,我们需要交换两个缓冲区,把绘制好的信息用于屏幕显示(否则无论怎么绘制,还是什么都看不到)。如果使用GLUT工具包,也可以很轻松的完成这一工作,只要在绘制完成时简单的调用glutSwapBuffers函数就可以了。
实现连续动画
似乎没有任何疑问,我们应该把绘制动画的代码写成下面这个样子:
for(i=0; ii)
{
DrawScene(i);
glutSwapBuffers();
Wait();
} 但事实上,这样做不太符合窗口系统的程序设计思路。还记得我们的第一个OpenGL程序吗?我们在main函数里写:
glutDisplayFunc(&myDisplay); 意思是对系统说:如果你需要绘制窗口了,请调用myDisplay这个函数。为什么我们不直接调用myDisplay,而要采用这种看似“舍近求远”的做法呢?原因在于——我们自己的程序无法掌握究竟什么时候该绘制窗口。因为一般的窗口系统——拿我们熟悉一点的来说——Windows和X窗口系统,都是支持同时显示多个窗口的。假如你的程序窗口碰巧被别的窗口遮住了,后来用户又把原来遮住的窗口移开,这时你的窗口需要重新绘制。很不幸的,你无法知道这一事件发生的具体时间。因此这一切只好委托操作系统来办了。
现在我们再看上面那个循环。既然DrawScene都可以交给操作系统来代办了,那让整个循环运行起来的工作是否也可以交给操作系统呢?答案是肯定的。我们先前的思路是:绘制,然后等待一段时间;再绘制,再等待一段时间。但如果去掉等待的时间,就变成了绘制,绘制,……,不停的绘制。——当然了,资源是公用的嘛,杀毒软件总要工作吧?我的下载不能停下来吧?我的mp3播放还不能给耽搁了。总不能因为我们的动画,让其他的工作都停下来。因此,我们需要在CPU空闲的时间绘制。
这里的“在CPU空闲的时间绘制”和我们在第一课讲的“在需要绘制的时候绘制”有些共通,都是“在XX时间做XX事”,GLUT工具包也提供了一个比较类似的函数:glutIdleFunc,表示在CPU空闲的时间调用某一函数。其实GLUT还提供了一些别的函数,例如“在键盘按下时做某事”等。
到现在,我们已经可以初步开始制作动画了。好的,就拿上次那个“太阳、地球和月亮”的程序开刀,让地球和月亮自己动起来。
#include 因为这个是动态的结果截图无意义,这里就不上图了。
关于垂直同步
代码是写好了,但相信大家还有疑问。某些朋友可能在运行时发现,虽然CPU几乎都用上了,但运动速度很快,根本看不清楚,另一些朋友在运行时发现CPU使用率很低,根本就没有把空闲时间完全利用起来。但对于上面那段代码来说,这些现象都是合理的。这里就牵涉到关于垂直同步的问题。
大家知道显示器的刷新率是比较有限的,一般为60~120Hz,也就是一秒钟刷新60~120次。但如果叫计算机绘制一个简单的画面,例如只有一个三角形,则一秒钟可以绘制成千上万次。因此,如果最大限度的利用计算机的处理能力,绘制很多幅画面,但显示器的刷新速度却跟不上,这不仅造成性能的浪费,还可能带来一些负面影响(例如,显示器只刷新到一半时,需要绘制的内容却变化了,由于显示器是逐行刷新的,于是显示器上半部分和下半部分实际上是来自两幅画面)。采用垂直同步技术可以解决这一问题。即,只有在显示器刷新时,才把绘制好的图象传输出去供显示。这样一来,计算机就不必去绘制大量的根本就用不到的图象了。如果显示器的刷新率为85Hz,则计算机一秒钟只需要绘制85幅图象就足够,如果场景足够简单,就会造成比较多的CPU空闲。
几乎所有的显卡都支持“垂直同步”这一功能。
垂直同步也有它的问题。如果刷新频率为60Hz,则在绘制比较简单的场景时,绘制一幅图画需要的时间很段,帧速可以恒定在60FPS(即60帧/秒)。如果场景变得复杂,绘制一幅图画的时间超过了1/60秒,则帧速将急剧下降。
如果绘制一幅图画的时间为1/50,则在第一个1/60秒时,显示器需要刷新了,但由于新的图画没有画好,所以只能显示原来的图画,等到下一个1/60秒时才显示新的图画。于是显示一幅图画实际上用了1/30秒,帧速为30FPS。(如果不采用垂直同步,则帧速应该是50FPS)如果绘制一幅图画的时间更长,则下降的趋势就是阶梯状的:60FPS,30FPS,20FPS,……(60/1,60/2,60/3,……)
如果每一幅图画的复杂程度是不一致的,且绘制它们需要的时间都在1/60上下。则在1/60时间内画完时,帧速为60FPS,在1/60时间未完成时,帧速为30FPS,这就造成了帧速的跳动。这是很麻烦的事情,需要避免它——要么想办法简化每一画面的绘制时间,要么都延迟一小段时间,以作到统一。
回过头来看前面的问题。如果使用了大量的CPU而且速度很快无法看清,则打开垂直同步可以解决该问题。当然如果你认为垂直同步有这样那样的缺点,也可以关闭它。——至于如何打开和关闭,因操作系统而异了。具体步骤请自己搜索之。
当然,也有其它办法可以控制动画的帧速,或者尽量让动画的速度尽量和帧速无关。不过这里面很多内容都是与操作系统比较紧密的,况且它们跟OpenGL关系也不太大。这里就不做介绍了。
计算帧速
不知道大家玩过3D Mark这个软件没有,它可以运行各种场景,测出帧速,并且为你的系统给出评分。这里我也介绍一个计算帧速的方法。
根据定义,帧速就是一秒钟内播放的画面数目(FPS)。我们可以先测量绘制两幅画面之间时间t,然后求它的倒数即可。假如t=0.05s,则FPS的值就是1/0.05=20。
理论上是如此了,可是如何得到这个时间呢?通常C语言的time函数精确度一般只到一秒,肯定是不行了。clock函数也就到十毫秒左右,还是有点不够。因为FPS为60和FPS为100的时候,t的值都是十几毫秒。
你知道如何测量一张纸的厚度吗?一个粗略的办法就是:用很多张纸叠在一起测厚度,计算平均值就可以了。我们这里也可以这样办。测量绘制50幅画面(包括垂直同步等因素的等待时间)需要的时间t’,由t’=t*50很容易的得到FPS=1/t=50/t’
下面这段代码可以统计该函数自身的调用频率,(原理就像上面说的那样),程序并不复杂,并且这并不属于OpenGL的内容,所以我不打算详细讲述它。
#include 最后,要把计算的帧速显示出来,但我们并没有学习如何使用OpenGL把文字显示到屏幕上。——但不要忘了,在我们的图形窗口背后,还有一个命令行窗口~使用printf函数就可以轻易的输出文字了。
#include 最后的一步,也被我们解决了——虽然做法不太雅观,没关系,以后我们还会改善它的。
时间过得太久,每次给的程序都只是一小段,一些朋友难免会出问题。
现在,我给出一个比较完整的程序,供大家参考。
小结:
OpenGL动画和传统意义上的动画相似,都是把画面一幅一幅的呈现在观众面前。一旦画面变换的速度快了,观众就会认为画面是连续的。
双缓冲技术是一种在计算机图形中普遍采用的技术,绝大多数OpenGL实现都支持双缓冲技术。
通常都是利用CPU空闲的时候绘制动画,但也可以有其它的选择。
介绍了垂直同步的相关知识。
介绍了一种简单的计算帧速(FPS)的方法。
最后,我们列出了一份完整的天体动画程序清单。
OpenGL入门学习[七]
今天要讲的是OpenGL光照的基本知识。虽然内容显得有点多,但条理还算比较清晰,理解起来应该没有困难。即使对于一些内容没有记住,问题也不大——光照部分是一个比较独立的内容,它的学习与其它方面的学习可以分开,不像视图变换那样,影响到许多方面。课程的最后给出了一个有关光照效果的动画演示程序,我想大家会喜欢的。
从生理学的角度上讲,眼睛之所以看见各种物体,是因为光线直接或间接的从它们那里到达了眼睛。人类对于光线强弱的变化的反应,比对于颜色变化的反应来得灵敏。因此对于人类而言,光线很大程度上表现了物体的立体感。
OpenGL对于光照效果提供了直接的支持,只需要调用某些函数,便可以实现简单的光照效果。但是在这之前,我们有必要了解一些基础知识。
建立光照模型
在现实生活中,某些物体本身就会发光,例如太阳、电灯等,而其它物体虽然不会发光,但可以反射来自其它物体的光。这些光通过各种方式传播,最后进入我们的眼睛——于是一幅画面就在我们的眼中形成了。
就目前的计算机而言,要准确模拟各种光线的传播,这是无法做到的事情。比如一个四面都是粗糙墙壁的房间,一盏电灯所发出的光线在很短的时间内就会经过非常多次的反射,最终几乎布满了房间的每一个角落,这一过程即使使用目前运算速度最快的计算机,也无法精确模拟。不过,我们并不需要精确的模拟各种光线,只需要找到一种近似的计算方式,使它的最终结果让我们的眼睛认为它是真实的,这就可以了。
OpenGL在处理光照时采用这样一种近似:把光照系统分为三部分,分别是光源、材质和光照环境。光源就是光的来源,可以是前面所说的太阳或者电灯等。材质是指接受光照的各种物体的表面,由于物体如何反射光线只由物体表面决定(OpenGL中没有考虑光的折射),材质特点就决定了物体反射光线的特点。光照环境是指一些额外的参数,它们将影响最终的光照画面,比如一些光线经过多次反射后,已经无法分清它究竟是由哪个光源发出,这时,指定一个“环境亮度”参数,可以使最后形成的画面更接近于真实情况。
在物理学中,光线如果射入理想的光滑平面,则反射后的光线是很规则的(这样的反射称为镜面反射)。光线如果射入粗糙的、不光滑的平面,则反射后的光线是杂乱的(这样的反射称为漫反射)。现实生活中的物体在反射光线时,并不是绝对的镜面反射或漫反射,但可以看成是这两种反射的叠加。对于光源发出的光线,可以分别设置其经过镜面反射和漫反射后的光线强度。对于被光线照射的材质,也可以分别设置光线经过镜面反射和漫反射后的光线强度。这些因素综合起来,就形成了最终的光照效果。
法线向量
根据光的反射定律,由光的入射方向和入射点的法线就可以得到光的出射方向。因此,对于指定的物体,在指定了光源后,即可计算出光的反射方向,进而计算出光照效果的画面。在OpenGL中,法线的方向是用一个向量来表示。
不幸的是,OpenGL并不会根据你所指定的多边形各个顶点来计算出这些多边形所构成的物体的表面的每个点的法线(这话听着有些迷糊),通常,为了实现光照效果,需要在代码中为每一个顶点指定其法线向量。
指定法线向量的方式与指定颜色的方式有雷同之处。在指定颜色时,只需要指定每一个顶点的颜色,OpenGL就可以自行计算顶点之间的其它点的颜色。并且,颜色一旦被指定,除非再指定新的颜色,否则以后指定的所有顶点都将以这一颜色作为自己的颜色。在指定法线向量时,只需要指定每一个顶点的法线向量,OpenGL会自行计算顶点之间的其它点的法线向量。并且,法线向量一旦被指定,除非再指定新的法线向量,否则以后指定的所有顶点都将以这一向量作为自己的法线向量。使用glColor*函数可以指定颜色,而使用glNormal*函数则可以指定法线向量。
注意:使用glTranslate*函数或者glRotate*函数可以改变物体的外观,但法线向量并不会随之改变。然而,使用glScale*函数,对每一坐标轴进行不同程度的缩放,很有可能导致法线向量的不正确,虽然OpenGL提供了一些措施来修正这一问题,但由此也带来了各种开销。因此,在使用了法线向量的场合,应尽量避免使用glScale*函数。即使使用,也最好保证各坐标轴进行等比例缩放。
控制光源
在OpenGL中,仅仅支持有限数量的光源。使用GL_LIGHT0表示第0号光源,GL_LIGHT1表示第1号光源,依次类推,OpenGL至少会支持8个光源,即GL_LIGHT0到GL_LIGHT7。使用glEnable函数可以开启它们。例如,glEnable(GL_LIGHT0);可以开启第0号光源。使用glDisable函数则可以关闭光源。一些OpenGL实现可能支持更多数量的光源,但总的来说,开启过多的光源将会导致程序运行速度的严重下降,玩过3D Mark的朋友可能多少也有些体会。一些场景中可能有成百上千的电灯,这时可能需要采取一些近似的手段来进行编程,否则以目前的计算机而言,是无法运行这样的程序的。
每一个光源都可以设置其属性,这一动作是通过glLight*函数完成的。glLight*函数具有三个参数,第一个参数指明是设置哪一个光源的属性,第二个参数指明是设置该光源的哪一个属性,第三个参数则是指明把该属性值设置成多少。光源的属性众多,下面将分别介绍。
(1)GL_AMBIENT、GL_DIFFUSE、GL_SPECULAR属性。这三个属性表示了光源所发出的光的反射特性(以及颜色)。每个属性由四个值表示,分别代表了颜色的R, G, B, A值。GL_AMBIENT表示该光源所发出的光,经过非常多次的反射后,最终遗留在整个光照环境中的强度(颜色)。GL_DIFFUSE表示该光源所发出的光,照射到粗糙表面时经过漫反射,所得到的光的强度(颜色)。GL_SPECULAR表示该光源所发出的光,照射到光滑表面时经过镜面反射,所得到的光的强度(颜色)。
(2)GL_POSITION属性。表示光源所在的位置。由四个值(X, Y, Z, W)表示。如果第四个值W为零,则表示该光源位于无限远处,前三个值表示了它所在的方向。这种光源称为方向性光源,通常,太阳可以近似的被认为是方向性光源。如果第四个值W不为零,则X/W, Y/W, Z/W表示了光源的位置。这种光源称为位置性光源。对于位置性光源,设置其位置与设置多边形顶点的方式相似,各种矩阵变换函数例如:glTranslate*、glRotate*等在这里也同样有效。方向性光源在计算时比位置性光源快了不少,因此,在视觉效果允许的情况下,应该尽可能的使用方向性光源。
(3)GL_SPOT_DIRECTION、GL_SPOT_EXPONENT、GL_SPOT_CUTOFF属性。表示将光源作为聚光灯使用(这些属性只对位置性光源有效)。很多光源都是向四面八方发射光线,但有时候一些光源则是只向某个方向发射,比如手电筒,只向一个较小的角度发射光线。GL_SPOT_DIRECTION属性有三个值,表示一个向量,即光源发射的方向。GL_SPOT_EXPONENT属性只有一个值,表示聚光的程度,为零时表示光照范围内向各方向发射的光线强度相同,为正数时表示光照向中央集中,正对发射方向的位置受到更多光照,其它位置受到较少光照。数值越大,聚光效果就越明显。
(4)GL_CONSTANT_ATTENUATION、GL_LINEAR_ATTENUATION、GL_QUADRATIC_ATTENUATION属性。这三个属性表示了光源所发出的光线的直线传播特性(这些属性只对位置性光源有效)。现实生活中,光线的强度随着距离的增加而减弱,OpenGL把这个减弱的趋势抽象成函数:
衰减因子 = 1 / (k1 + k2 * d + k3 * k3 * d) 其中d表示距离,光线的初始强度乘以衰减因子,就得到对应距离的光线强度。k1,k2,k3分别就是GL_CONSTANT_ATTENUATION, GL_LINEAR_ATTENUATION, GL_QUADRATIC_ATTENUATION。通过设置这三个常数,就可以控制光线在传播过程中的减弱趋势。属性还真是不少。当然了,如果是使用方向性光源,(3)(4)这两类属性就不会用到了,问题就变得简单明了。
控制材质
材质与光源相似,也需要设置众多的属性。不同的是,光源是通过glLight*函数来设置的,而材质则是通过glMaterial*函数来设置的。
glMaterial*函数有三个参数。第一个参数表示指定哪一面的属性。可以是GL_FRONT、GL_BACK或者GL_FRONT_AND_BACK。分别表示设置“正面”“背面”的材质,或者两面同时设置。(关于“正面”“背面”的内容需要参看前些课程的内容)第二、第三个参数与glLight*函数的第二、三个参数作用类似。下面分别说明glMaterial*函数可以指定的材质属性。
(1)GL_AMBIENT、GL_DIFFUSE、GL_SPECULAR属性。这三个属性与光源的三个对应属性类似,每一属性都由四个值组成。GL_AMBIENT表示各种光线照射到该材质上,经过很多次反射后最终遗留在环境中的光线强度(颜色)。GL_DIFFUSE表示光线照射到该材质上,经过漫反射后形成的光线强度(颜色)。GL_SPECULAR表示光线照射到该材质上,经过镜面反射后形成的光线强度(颜色)。通常,GL_AMBIENT和GL_DIFFUSE都取相同的值,可以达到比较真实的效果。使用GL_AMBIENT_AND_DIFFUSE可以同时设置GL_AMBIENT和GL_DIFFUSE属性。
(2)GL_SHININESS属性。该属性只有一个值,称为“镜面指数”,取值范围是0到128。该值越小,表示材质越粗糙,点光源发射的光线照射到上面,也可以产生较大的亮点。该值越大,表示材质越类似于镜面,光源照射到上面后,产生较小的亮点。
(3)GL_EMISSION属性。该属性由四个值组成,表示一种颜色。OpenGL认为该材质本身就微微的向外发射光线,以至于眼睛感觉到它有这样的颜色,但这光线又比较微弱,以至于不会影响到其它物体的颜色。
(4)GL_COLOR_INDEXES属性。该属性仅在颜色索引模式下使用,由于颜色索引模式下的光照比RGBA模式要复杂,并且使用范围较小,这里不做讨论。
选择光照模型
这里所说的“光照模型”是OpenGL的术语,它相当于我们在前面提到的“光照环境”。在OpenGL中,光照模型包括四个部分的内容:全局环境光线(即那些充分散射,无法分清究竟来自哪个光源的光线)的强度、观察点位置是在较近位置还是在无限远处、物体正面与背面是否分别计算光照、镜面颜色(即GL_SPECULAR属性所指定的颜色)的计算是否从其它光照计算中分离出来,并在纹理操作以后在进行应用。
以上四方面的内容都通过同一个函数glLightModel*来进行设置。该函数有两个参数,第一个表示要设置的项目,第二个参数表示要设置成的值。
GL_LIGHT_MODEL_AMBIENT表示全局环境光线强度,由四个值组成。
GL_LIGHT_MODEL_LOCAL_VIEWER表示是否在近处观看,若是则设置为GL_TRUE,否则(即在无限远处观看)设置为GL_FALSE。
GL_LIGHT_MODEL_TWO_SIDE表示是否执行双面光照计算。如果设置为GL_TRUE,则OpenGL不仅将根据法线向量计算正面的光照,也会将法线向量反转并计算背面的光照。
GL_LIGHT_MODEL_COLOR_CONTROL表示颜色计算方式。如果设置为GL_SINGLE_COLOR,表示按通常顺序操作,先计算光照,再计算纹理。如果设置为GL_SEPARATE_SPECULAR_COLOR,表示将>GL_SPECULAR属性分离出来,先计算光照的其它部分,待纹理操作完成后再计算GL_SPECULAR。后者通常可以使画面效果更为逼真(当然,如果本身就没有执行任何纹理操作,这样的分离就没有任何意义)。
最后的准备
到现在可以说是完事俱备了。不过,OpenGL默认是关闭光照处理的。要打开光照处理功能,使用下面的语句:
glEnable(GL_LIGHTING);要关闭光照处理功能,使用glDisable(GL_LIGHTING);即可。
示例程序
到现在,我们已经可以编写简单的使用光照的OpenGL程序了。
我们仍然以太阳、地球作为例子(这次就不考虑月亮了^-^),把太阳作为光源,模拟地球围绕太阳转动时光照的变化。于是,需要设置一个光源——太阳,设置两种材质——太阳的材质和地球的材质。把太阳光线设置为白色,位置在画面正中。把太阳的材质设置为微微散发出红色的光芒,把地球的材质设置为微微散发出暗淡的蓝色光芒,并且反射蓝色的光芒,镜面指数设置成一个比较小的值。简单起见,不再考虑太阳和地球的大小关系,用同样大小的球体来代替之。
关于法线向量。球体表面任何一点的法线向量,就是球心到该点的向量。如果使用glutSolidSphere函数来绘制球体,则该函数会自动的指定这些法线向量,不必再手工指出。如果是自己指定若干的顶点来绘制一个球体,则需要自己指定法线响亮。
由于我们使用的太阳是一个位置性光源,在设置它的位置时,需要利用到矩阵变换。因此,在设置光源的位置以前,需要先设置好各种矩阵。利用gluPerspective函数来创建具有透视效果的视图。我们也将利用前面课程所学习的动画知识,让整个画面动起来。
下面给出具体的代码:
#include 小结:
本课介绍了OpenGL光照的基本知识。OpenGL把光照分解为光源、材质、光照模式三个部分,根据这三个部分的各种信息,以及物体表面的法线向量,可以计算得到最终的光照效果。
光源、材质和光照模式都有各自的属性,尽管属性种类繁多,但这些属性都只用很少的几个函数来设置。使用glLight*函数可设置光源的属性,使用glMaterial*函数可设置材质的属性,使用glLightModel*函数可设置光照模式。
GL_AMBIENT、GL_DIFFUSE、GL_SPECULAR这三种属性是光源和材质所共有的,如果某光源发出的光线照射到某材质的表面,则最终的漫反射强度由两个GL_DIFFUSE属性共同决定,最终的镜面反射强度由两个GL_SPECULAR属性共同决定。
可以使用多个光源来实现各种逼真的效果,然而,光源数量的增加将造成程序运行速度的明显下降。
在使用OpenGL光照过程中,属性的种类和数量都非常繁多,通常,需要很多的经验才可以熟练的设置各种属性,从而形成逼真的光照效果。(各位也看到了,其实这个课程的示例程序中,属性设置也不怎么好)。然而,设置这些属性的艺术性远远超过了技术性,往往是一些美术制作人员设置好各种属性(并保存为文件),然后由程序员编写的程序去执行绘制工作。因此,即使目前无法熟练运用各种属性,也不必过于担心。如果条件允许,可以玩玩类似3DS MAX之类的软件,对理解光照、熟悉各种属性设置会有一些帮助。
在课程的最后,我们给出了一个样例程序,演示了太阳和地球模型中的光照效果。
OpenGL入门学习[八]
今天介绍关于OpenGL显示列表的知识。本课内容并不多,但需要一些理解能力。在学习时,可以将显示列表与C语言的“函数”进行类比,加深体会。
我们已经知道,使用OpenGL其实只要调用一系列的OpenGL函数就可以了。然而,这种方式在一些时候可能导致问题。比如某个画面中,使用了数千个多边形来表现一个比较真实的人物,OpenGL为了产生这数千个多边形,就需要不停的调用glVertex*函数,每一个多边形将至少调用三次(因为多边形至少有三个顶点),于是绘制一个比较真实的人物就需要调用上万次的glVertex*函数。更糟糕的是,如果我们需要每秒钟绘制60幅画面,则每秒调用的glVertex*函数次数就会超过数十万次,乃至接近百万次。这样的情况是我们所不愿意看到的。
同时,考虑这样一段代码:
const int segments = 100;
const GLfloat pi = 3.14f;
int i;
glLineWidth(10.0);
glBegin(GL_LINE_LOOP);
for(i=0; i2 * pi * i / segments;
glVertex2f(cos(tmp), sin(tmp));
}
glEnd(); 这段代码将绘制一个圆环。如果我们在每次绘制图象时调用这段代码,则虽然可以达到绘制圆环的目的,但是cos、sin等开销较大的函数被多次调用,浪费了CPU资源。如果每一个顶点不是通过cos、sin等函数得到,而是使用更复杂的运算方式来得到,则浪费的现象就更加明显。
经过分析,我们可以发现上述两个问题的共同点:程序多次执行了重复的工作,导致CPU资源浪费和运行速度的下降。使用显示列表可以较好的解决上述两个问题。
在编写程序时,遇到重复的工作,我们往往是将重复的工作编写为函数,在需要的地方调用它。类似的,在编写OpenGL程序时,遇到重复的工作,可以创建一个显示列表,把重复的工作装入其中,并在需要的地方调用这个显示列表。
使用显示列表一般有四个步骤:分配显示列表编号、创建显示列表、调用显示列表、销毁显示列表。
分配显示列表编号
OpenGL允许多个显示列表同时存在,就好象C语言允许程序中有多个函数同时存在。C语言中,不同的函数用不同的名字来区分,而在OpenGL中,不同的显示列表用不同的正整数来区分。
你可以自己指定一些各不相同的正整数来表示不同的显示列表。但是如果你不够小心,可能出现一个显示列表将另一个显示列表覆盖的情况。为了避免这一问题,使用glGenLists函数来自动分配一个没有使用的显示列表编号。
glGenLists函数有一个参数i,表示要分配i个连续的未使用的显示列表编号。返回的是分配的若干连续编号中最小的一个。例如,glGenLists(3);如果返回20,则表示分配了20、21、22这三个连续的编号。如果函数返回零,表示分配失败。
可以使用glIsList函数判断一个编号是否已经被用作显示列表。
创建显示列表
创建显示列表实际上就是把各种OpenGL函数的调用装入到显示列表中。使用glNewList开始装入,使用glEndList结束装入。glNewList有两个参数,第一个参数是一个正整数表示装入到哪个显示列表。第二个参数有两种取值,如果为GL_COMPILE,则表示以下的内容只是装入到显示列表,但现在不执行它们;如果为GL_COMPILE_AND_EXECUTE,表示在装入的同时,把装入的内容执行一遍。
例如,需要把“设置颜色为红色,并且指定一个坐标为(0, 0)的顶点”这两条命令装入到编号为list的显示列表中,并且在装入的时候不执行,则可以用下面的代码:
glNewList(list, GL_COMPILE);
glColor3f(1.0f, 0.0f, 0.0f);
glVertex2f(0.0f, 0.0f);
glEnd();注意:显示列表只能装入OpenGL函数,而不能装入其它内容。例如:
int i = 3;
glNewList(list, GL_COMPILE);
if( i > 20 )
glColor3f(1.0f, 0.0f, 0.0f);
glVertex2f(0.0f, 0.0f);
glEnd();其中if这个判断就没有被装入到显示列表。以后即使修改i的值,使i>20的条件成立,则glColor3f这个函数也不会被执行。因为它根本就不存在于显示列表中。
另外,并非所有的OpenGL函数都可以装入到显示列表中。例如,各种用于查询的函数,它们无法被装入到显示列表,因为它们都具有返回值,而glCallList和glCallLists函数都不知道如何处理这些返回值。在网络方式下,设置客户端状态的函数也无法被装入到显示列表,这是因为显示列表被保存到服务器端,各种设置客户端状态的函数在发送到服务器端以前就被执行了,而服务器端无法执行这些函数。分配、创建、删除显示列表的动作也无法被装入到另一个显示列表,但调用显示列表的动作则可以被装入到另一个显示列表。
调用显示列表
使用glCallList函数可以调用一个显示列表。该函数有一个参数,表示要调用的显示列表的编号。例如,要调用编号为10的显示列表,直接使用glCallList(10);就可以了。
使用glCallLists函数可以调用一系列的显示列表。该函数有三个参数,第一个参数表示了要调用多少个显示列表。第二个参数表示了这些显示列表的编号的储存格式,可以是GL_BYTE(每个编号用一个GLbyte表示),GL_UNSIGNED_BYTE(每个编号用一个GLubyte表示),GL_SHORT,GL_UNSIGNED_SHORT,GL_INT,GL_UNSIGNED_INT,GL_FLOAT。第三个参数表示了这些显示列表的编号所在的位置。在使用该函数前,需要用glListBase函数来设置一个偏移量。假设偏移量为k,且glCallLists中要求调用的显示列表编号依次为l1, l2, l3, …,则实际调用的显示列表为l1+k, l2+k, l3+k, …。
例如:
GLuint lists[] = {1, 3, 4, 8};
glListBase(10);
glCallLists(4, GL_UNSIGNED_INT, lists);则实际上调用的是编号为11, 13, 14, 18的四个显示列表。
注:“调用显示列表”这个动作本身也可以被装在另一个显示列表中。
销毁显示列表
销毁显示列表可以回收资源。使用glDeleteLists来销毁一串编号连续的显示列表。
例如,使用glDeleteLists(20, 4);将销毁20,21,22,23这四个显示列表。
使用显示列表将会带来一些开销,例如,把各种动作保存到显示列表中会占用一定数量的内存资源。但如果使用得当,显示列表可以提升程序的性能。这主要表现在以下方面:
- 1 明显的减少OpenGL函数的调用次数。如果函数调用是通过网络进行的(Linux等操作系统支持这样的方式,即由应用程序在客户端发出OpenGL请求,由网络上的另一台服务器进行实际的绘图操作),将显示列表保存在服务器端,可以大大减少网络负担。
- 2 保存中间结果,避免一些不必要的计算。例如前面的样例程序中,cos、sin函数的计算结果被直接保存到显示列表中,以后使用时就不必重复计算。
- 3 便于优化。我们已经知道,使用
glTranslate*、glRotate*、glScale*等函数时,实际上是执行矩阵乘法操作,由于这些函数经常被组合在一起使用,通常会出现矩阵的连乘。这时,如果把这些操作保存到显示列表中,则一些复杂的OpenGL版本会尝试先计算出连乘的一部分结果,从而提高程序的运行速度。在其它方面也可能存在类似的例子。
同时,显示列表也为程序的设计带来方便。我们在设置一些属性时,经常把一些相关的函数放在一起调用,(比如,把设置光源的各种属性的函数放到一起)这时,如果把这些设置属性的操作装入到显示列表中,则可以实现属性的成组的切换。
当然了,即使使用显示列表在某些情况下可以提高性能,但这种提高很可能并不明显。毕竟,在硬件配置和大致的软件算法都不变的前提下,性能可提升的空间并不大。
显示列表的内容就是这么多了,下面我们看一个例子。
假设我们需要绘制一个旋转的彩色正四面体,则可以这样考虑:设置一个全局变量angle,然后让它的值不断的增加(到达360后又恢复为0,周而复始)。每次需要绘制图形时,根据angle的值进行旋转,然后绘制正四面体。这里正四面体采用显示列表来实现,即把绘制正四面体的若干OpenGL函数装到一个显示列表中,然后每次需要绘制时,调用这个显示列表即可。
将正四面体的四个顶点颜色分别设置为红、黄、绿、蓝,通过数学计算,将坐标设置为:
A点:( 0.5, -sqrt(6)/12, -sqrt(3)/6)
B点:( -0.5, -sqrt(6)/12, -sqrt(3)/6)
C点:( 0, -sqrt(6)/12, sqrt(3)/3)
D点:( 0, sqrt(6)/4, 0)程序代码中也做了相应的修改
下面给出程序代码,大家可以从中体会一下显示列表的用法。
#include 在程序中,我们将绘制正四面体的OpenGL函数装到了一个显示列表中,但是,关于旋转的操作却在显示列表之外进行。这是因为如果把旋转的操作也装入到显示列表,则每次旋转的角度都是一样的,不会随着angle的值的变化而变化,于是就不能表现出动态的旋转效果了。
程序运行时,可能感觉到画面的立体感不足,这主要是因为没有使用光照的缘故。如果将glColor3fv函数去掉,改为设置各种材质,然后开启光照效果,则可以产生更好的立体感。大家可以自己试着使用光照效果,唯一需要注意的地方就是法线向量的计算。由于这里的正四面体四个顶点坐标选取得比较特殊,使得正四面体的中心坐标正好是(0, 0, 0),因此,每三个顶点坐标的平均值正好就是这三个顶点所组成的平面的法线向量的值。
void setNormal(GLfloat* Point1, GLfloat* Point2, GLfloat* Point3)
{
GLfloat normal[3];
int i;
for(i=0; i<3; ++i)
normal[i] = (Point1[i]+Point2[i]+Point3[i]) / 3;
glNormal3fv(normal);
}限于篇幅,这里就不给出完整的程序了。不过,大家可以自行尝试,看看使用光照后效果有何种改观。尤其是注意四面体各个表面交界的位置,在未使用光照前,几乎看不清轮廓,在使用光照后,可比较容易的区分各个平面,因此立体感得到加强。
当然了,这样的效果还不够。如果在各表面的交界处设置很多细小的平面,进行平滑处理,则光照后的效果将更真实。但这已经远离本课的内容了。
小结
本课介绍了显示列表的知识和简单的应用。
可以把各种OpenGL函数调用的动作装到显示列表中,以后调用显示列表,就相当于调用了其中的OpenGL函数。显示列表中除了存放对OpenGL函数的调用外,不会存放其它内容。
使用显示列表的过程是:分配一个未使用的显示列表编号,把OpenGL函数调用装入显示列表,调用显示列表,销毁显示列表。
使用显示列表有可能带来程序运行速度的提升,但是这种提升并不一定会很明显。显示列表本身也存在一定的开销。
把绘制固定的物体的OpenGL函数放到一个显示列表中,是一种不错的编程思路。本课最后的例子中使用了这种思路。
OpenGL入门学习[九]
今天介绍关于OpenGL混合的基本知识。混合是一种常用的技巧,通常可以用来实现半透明。但其实它也是十分灵活的,你可以通过不同的设置得到不同的混合结果,产生一些有趣或者奇怪的图象。
混合是什么呢?混合就是把两种颜色混在一起。具体一点,就是把某一像素位置原来的颜色和将要画上去的颜色,通过某种方式混在一起,从而实现特殊的效果。
假设我们需要绘制这样一个场景:透过红色的玻璃去看绿色的物体,那么可以先绘制绿色的物体,再绘制红色玻璃。在绘制红色玻璃的时候,利用“混合”功能,把将要绘制上去的红色和原来的绿色进行混合,于是得到一种新的颜色,看上去就好像玻璃是半透明的。
要使用OpenGL的混合功能,只需要调用:glEnable(GL_BLEND);即可。
要关闭OpenGL的混合功能,只需要调用:glDisable(GL_BLEND);即可。
注意:只有在RGBA模式下,才可以使用混合功能,颜色索引模式下是无法使用混合功能的。
源因子和目标因子
前面我们已经提到,混合需要把原来的颜色和将要画上去的颜色找出来,经过某种方式处理后得到一种新的颜色。这里把将要画上去的颜色称为“源颜色”,把原来的颜色称为“目标颜色”。
OpenGL会把源颜色和目标颜色各自取出,并乘以一个系数(源颜色乘以的系数称为“源因子”,目标颜色乘以的系数称为“目标因子”),然后相加,这样就得到了新的颜色。(也可以不是相加,新版本的OpenGL可以设置运算方式,包括加、减、取两者中较大的、取两者中较小的、逻辑运算等,但我们这里为了简单起见,不讨论这个了)
下面用数学公式来表达一下这个运算方式。假设源颜色的四个分量(指红色,绿色,蓝色,alpha值)是(Rs, Gs, Bs, As),目标颜色的四个分量是(Rd, Gd, Bd, Ad),又设源因子为(Sr, Sg, Sb, Sa),目标因子为(Dr, Dg, Db, Da)。则混合产生的新颜色可以表示为:
(Rs*Sr+Rd*Dr, Gs*Sg+Gd*Dg, Bs*Sb+Bd*Db, As*Sa+Ad*Da)当然了,如果颜色的某一分量超过了1.0,则它会被自动截取为1.0,不需要考虑越界的问题。
源因子和目标因子是可以通过glBlendFunc函数来进行设置的。glBlendFunc有两个参数,前者表示源因子,后者表示目标因子。这两个参数可以是多种值,下面介绍比较常用的几种。
GL_ZERO: 表示使用0.0作为因子,实际上相当于不使用这种颜色参与混合运算。
GL_ONE: 表示使用1.0作为因子,实际上相当于完全的使用了这种颜色参与混合运算。
GL_SRC_ALPHA:表示使用源颜色的alpha值来作为因子。
GL_DST_ALPHA:表示使用目标颜色的alpha值来作为因子。
GL_ONE_MINUS_SRC_ALPHA:表示用1.0减去源颜色的alpha值来作为因子。
GL_ONE_MINUS_DST_ALPHA:表示用1.0减去目标颜色的alpha值来作为因子。
除此以外,还有GL_SRC_COLOR(把源颜色的四个分量分别作为因子的四个分量)、GL_ONE_MINUS_SRC_COLOR、GL_DST_COLOR、GL_ONE_MINUS_DST_COLOR等,前两个在OpenGL旧版本中只能用于设置目标因子,后两个在OpenGL旧版本中只能用于设置源因子。新版本的OpenGL则没有这个限制,并且支持新的GL_CONST_COLOR(设定一种常数颜色,将其四个分量分别作为因子的四个分量)、GL_ONE_MINUS_CONST_COLOR、GL_CONST_ALPHA、GL_ONE_MINUS_CONST_ALPHA。另外还有GL_SRC_ALPHA_SATURATE。新版本的OpenGL还允许颜色的alpha值和RGB值采用不同的混合因子。但这些都不是我们现在所需要了解的。毕竟这还是入门教材,不需要整得太复杂~
举例来说:
如果设置了glBlendFunc(GL_ONE, GL_ZERO); 则表示完全使用源颜色,完全不使用目标颜色,因此画面效果和不使用混合的时候一致(当然效率可能会低一点点)。如果没有设置源因子和目标因子,则默认情况就是这样的设置。
如果设置了glBlendFunc(GL_ZERO, GL_ONE);,则表示完全不使用源颜色,因此无论你想画什么,最后都不会被画上去了。(但这并不是说这样设置就没有用,有些时候可能有特殊用途)
如果设置了glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);,则表示源颜色乘以自身的alpha值,目标颜色乘以1.0减去源颜色的alpha值,这样一来,源颜色的alpha值越大,则产生的新颜色中源颜色所占比例就越大,而目标颜色所占比例则减小。这种情况下,我们可以简单的将源颜色的alpha值理解为“不透明度”。这也是混合时最常用的方式。
如果设置了glBlendFunc(GL_ONE, GL_ONE);则表示完全使用源颜色和目标颜色,最终的颜色实际上就是两种颜色的简单相加。例如红色(1, 0, 0)和绿色(0, 1, 0)相加得到(1, 1, 0),结果为黄色。
注意:
所谓源颜色和目标颜色,是跟绘制的顺序有关的。假如先绘制了一个红色的物体,再在其上绘制绿色的物体。则绿色是源颜色,红色是目标颜色。如果顺序反过来,则红色就是源颜色,绿色才是目标颜色。在绘制时,应该注意顺序,使得绘制的源颜色与设置的源因子对应,目标颜色与设置的目标因子对应。不要被混乱的顺序搞晕了。
二维图形混合举例
下面看一个简单的例子,实现将两种不同的颜色混合在一起。为了便于观察,我们绘制两个矩形:glRectf(-1, -1, 0.5, 0.5);glRectf(-0.5, -0.5, 1, 1);,这两个矩形有一个重叠的区域,便于我们观察混合的效果。
先来看看使用glBlendFunc(GL_ONE, GL_ZERO);的它的结果与不使用混合时相同。
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT);
glEnable(GL_BLEND);
glBlendFunc(GL_ONE, GL_ZERO);
glColor4f(1, 0, 0, 0.5);
glRectf(-1, -1, 0.5, 0.5);
glColor4f(0, 1, 0, 0.5);
glRectf(-0.5, -0.5, 1, 1);
glutSwapBuffers();
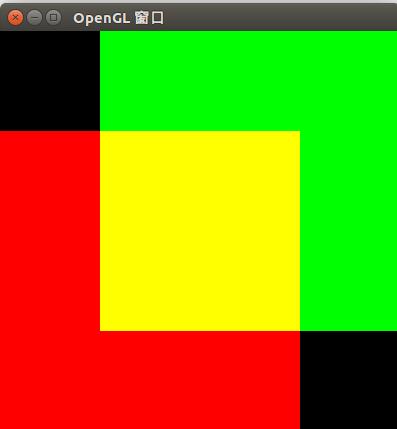
}尝试把glBlendFunc的参数修改为
glBlendFunc(GL_SRC_ALPHA,GL_ONE_MINUS_SRC_ALPHA);
glBlendFunc(GL_ONE, GL_ONE); 观察效果。第一种情况下,效果与没有使用混合时相同,后绘制的图形会覆盖先绘制的图形。第二种情况下,alpha被当作“不透明度”,由于被设置为0.5,所以两个矩形看上去都是半透明的,乃至于看到黑色背景。第三种是将颜色相加,红色和绿色相加得到黄色。
第一种情况:

第二种情况:
实现三维混合
也许你迫不及待的想要绘制一个三维的带有半透明物体的场景了。但是现在恐怕还不行,还有一点是在进行三维场景的混合时必须注意的,那就是深度缓冲。
深度缓冲是这样一段数据,它记录了每一个像素距离观察者有多近。在启用深度缓冲测试的情况下,如果将要绘制的像素比原来的像素更近,则像素将被绘制。否则,像素就会被忽略掉,不进行绘制。这在绘制不透明的物体时非常有用——不管是先绘制近的物体再绘制远的物体,还是先绘制远的物体再绘制近的物体,或者干脆以混乱的顺序进行绘制,最后的显示结果总是近的物体遮住远的物体。
然而在你需要实现半透明效果时,发现一切都不是那么美好了。如果你绘制了一个近距离的半透明物体,则它在深度缓冲区内保留了一些信息,使得远处的物体将无法再被绘制出来。虽然半透明的物体仍然半透明,但透过它看到的却不是正确的内容了。
要解决以上问题,需要在绘制半透明物体时将深度缓冲区设置为只读,这样一来,虽然半透明物体被绘制上去了,深度缓冲区还保持在原来的状态。如果再有一个物体出现在半透明物体之后,在不透明物体之前,则它也可以被绘制(因为此时深度缓冲区中记录的是那个不透明物体的深度)。以后再要绘制不透明物体时,只需要再将深度缓冲区设置为可读可写的形式即可。嗯?你问我怎么绘制一个一部分半透明一部分不透明的物体?这个好办,只需要把物体分为两个部分,一部分全是半透明的,一部分全是不透明的,分别绘制就可以了。
即使使用了以上技巧,我们仍然不能随心所欲的按照混乱顺序来进行绘制。必须是先绘制不透明的物体,然后绘制透明的物体。否则,假设背景为蓝色,近处一块红色玻璃,中间一个绿色物体。如果先绘制红色半透明玻璃的话,它先和蓝色背景进行混合,则以后绘制中间的绿色物体时,想单独与红色玻璃混合已经不能实现了。
总结起来,绘制顺序就是:首先绘制所有不透明的物体。如果两个物体都是不透明的,则谁先谁后都没有关系。然后,将深度缓冲区设置为只读。接下来,绘制所有半透明的物体。如果两个物体都是半透明的,则谁先谁后只需要根据自己的意愿(注意了,先绘制的将成为“目标颜色”,后绘制的将成为“源颜色”,所以绘制的顺序将会对结果造成一些影响)。最后,将深度缓冲区设置为可读可写形式。
调用glDepthMask(GL_FALSE);可将深度缓冲区设置为只读形式。调用glDepthMask(GL_TRUE);可将深度缓冲区设置为可读可写形式。
一些网上的教程,包括大名鼎鼎的NeHe教程,都在使用三维混合时直接将深度缓冲区禁用,即调用glDisable(GL_DEPTH_TEST);。这样做并不正确。如果先绘制一个不透明的物体,再在其背后绘制半透明物体,本来后面的半透明物体将不会被显示(被不透明的物体遮住了),但如果禁用深度缓冲,则它仍然将会显示,并进行混合。NeHe提到某些显卡在使用glDepthMask函数时可能存在一些问题,但可能是由于我的阅历有限,并没有发现这样的情况。
那么,实际的演示一下吧。我们来绘制一些半透明和不透明的球体。假设有三个球体,一个红色不透明的,一个绿色半透明的,一个蓝色半透明的。红色最远,绿色在中间,蓝色最近。根据前面所讲述的内容,红色不透明球体必须首先绘制,而绿色和蓝色则可以随意修改顺序。这里为了演示不注意设置深度缓冲的危害,我们故意先绘制最近的蓝色球体,再绘制绿色球体。
为了让这些球体有一点立体感,我们使用光照。在(1, 1, -1)处设置一个白色的光源。代码如下:
void setLight(void)
{
static const GLfloat light_position[] = {1.0f, 1.0f, -1.0f, 1.0f};
static const GLfloat light_ambient[] = {0.2f, 0.2f, 0.2f, 1.0f};
static const GLfloat light_diffuse[] = {1.0f, 1.0f, 1.0f, 1.0f};
static const GLfloat light_specular[] = {1.0f, 1.0f, 1.0f, 1.0f};
glLightfv(GL_LIGHT0, GL_POSITION, light_position);
glLightfv(GL_LIGHT0, GL_AMBIENT, light_ambient);
glLightfv(GL_LIGHT0, GL_DIFFUSE, light_diffuse);
glLightfv(GL_LIGHT0, GL_SPECULAR, light_specular);
glEnable(GL_LIGHT0);
glEnable(GL_LIGHTING);
glEnable(GL_DEPTH_TEST);
}每一个球体颜色不同。所以它们的材质也都不同。这里用一个函数来设置材质。
void setMatirial(const GLfloat mat_diffuse[4], GLfloat mat_shininess)
{
static const GLfloat mat_specular[] = {0.0f, 0.0f, 0.0f, 1.0f};
static const GLfloat mat_emission[] = {0.0f, 0.0f, 0.0f, 1.0f};
glMaterialfv(GL_FRONT, GL_AMBIENT_AND_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_EMISSION, mat_emission);
glMaterialf (GL_FRONT, GL_SHININESS, mat_shininess);
}有了这两个函数,我们就可以根据前面的知识写出整个程序代码了。这里只给出了绘制的部分,其它部分大家可以自行完成。
void myDisplay(void)
{
// 定义一些材质颜色
const static GLfloat red_color[] = {1.0f, 0.0f, 0.0f, 1.0f};
const static GLfloat green_color[] = {0.0f, 1.0f, 0.0f, 0.3333f};
const static GLfloat blue_color[] = {0.0f, 0.0f, 1.0f, 0.5f};
// 清除屏幕
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
// 启动混合并设置混合因子
glEnable(GL_BLEND);
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
// 设置光源
setLight();
// 以(0, 0, 0.5)为中心,绘制一个半径为.3的不透明红色球体(离观察者最远)
setMatirial(red_color, 30.0);
glPushMatrix();
glTranslatef(0.0f, 0.0f, 0.5f);
glutSolidSphere(0.3, 30, 30);
glPopMatrix();
// 下面将绘制半透明物体了,因此将深度缓冲设置为只读
glDepthMask(GL_FALSE);
// 以(0.2, 0, -0.5)为中心,绘制一个半径为.2的半透明蓝色球体(离观察者最近)
setMatirial(blue_color, 30.0);
glPushMatrix();
glTranslatef(0.2f, 0.0f, -0.5f);
glutSolidSphere(0.2, 30, 30);
glPopMatrix();
// 以(0.1, 0, 0)为中心,绘制一个半径为.15的半透明绿色球体(在前两个球体之间)
setMatirial(green_color, 30.0);
glPushMatrix();
glTranslatef(0.1, 0, 0);
glutSolidSphere(0.15, 30, 30);
glPopMatrix();
// 完成半透明物体的绘制,将深度缓冲区恢复为可读可写的形式
glDepthMask(GL_TRUE);
glutSwapBuffers();
} 大家也可以将上面两处glDepthMask删去,结果会看到最近的蓝色球虽然是半透明的,但它的背后直接就是红色球了,中间的绿色球没有被正确绘制。(我经过测试发现不是这样的,和原来的显示一样,是不是因为版本改变了??)
小结:
本课介绍了OpenGL混合功能的相关知识。
混合就是在绘制时,不是直接把新的颜色覆盖在原来旧的颜色上,而是将新的颜色与旧的颜色经过一定的运算,从而产生新的颜色。新的颜色称为源颜色,原来旧的颜色称为目标颜色。传统意义上的混合,是将源颜色乘以源因子,目标颜色乘以目标因子,然后相加。
源因子和目标因子是可以设置的。源因子和目标因子设置的不同直接导致混合结果的不同。将源颜色的alpha值作为源因子,用1.0减去源颜色alpha值作为目标因子,是一种常用的方式。这时候,源颜色的alpha值相当于“不透明度”的作用。利用这一特点可以绘制出一些半透明的物体。
在进行混合时,绘制的顺序十分重要。因为在绘制时,正要绘制上去的是源颜色,原来存在的是目标颜色,因此先绘制的物体就成为目标颜色,后来绘制的则成为源颜色。绘制的顺序要考虑清楚,将目标颜色和设置的目标因子相对应,源颜色和设置的源因子相对应。
在进行三维混合时,不仅要考虑源因子和目标因子,还应该考虑深度缓冲区。必须先绘制所有不透明的物体,再绘制半透明的物体。在绘制半透明物体时前,还需要将深度缓冲区设置为只读形式,否则可能出现画面错误。
/*****************************************************************************/
转来的东西,原文是在windows上开发,这里在linux下稍作修改就能跑起来。
这里不是为了弄出绚丽的3D效果,而是让opengl也能在skyworth平台上跑起来。
/*****************************************************************************/