类脑运算--脉冲神经网络（Spiking Neural Network）叙述

Spiking Neural Network简述（一）

传统神经网络包括现存的各种以perceptron为基本单元的拓扑变种， 比如卷积神经网络系列（CNNs), 循环神经网络系列（RNNs）, 生成对抗网络（GANs）， 自编码器（Autoencoders) 等等。 因为反向传播算法的存在和各类数学优化器的发展， 使得第二代神经网络在各项任务上有着出色的表现。

Spiking Neural Network(SNN) 被公认为继现有的MLP为基础的第二代神经网络(ANN)之后发展的第三代神经网络。虽然传统神经网络已然在各项任务上取得了优异的成绩， 但它们的原理和运算过程仍然和真正的人脑信息处理过程依然相差甚远。主要的差异可以总结为以下几点：

1. 传统神经网络算法仍然依据于使用高精度的浮点数进行运算， 然而人脑并不会使用浮点数进行运算。 在人的传感系统和大脑中， 信息会以动作电压或称之为电脉冲（electric spike）的形式传递，接受，和处理。
2. ANN的训练过程对反向传播算法（梯度下降)的依赖程度非常之高， 然而在真实的人脑学习过程中，科学家们还没有观察到这种学习类型。 更多的， 人脑的记忆和学习依赖于突触后细胞受到刺激后所产生的突触可塑性。 详见： Hebbian learning
3. ANN通常需要大量的标签数据集来驱动网络的拟合。 这与我们平时经理的有所不同。 我们在很多情况下的感知和学习过程都是非监督式的。并且， 人脑通常不需要如此大量反复的数据来学习同一件事情。

综上所述， 为了使神经网络更加接近于人脑， SNN随而诞生了。发现它的灵感，就来自于生物大脑处理信息的方式—spikes。 读到这里，就应该已经明白SNN并不是一个像CNN,RNN这样的网络结构， 而是一个新型的，更加接近人脑的一种神经网络算法的统称。

SNN和ANN的区别

那么， SNN和传统方法的区别在哪里呢？

1，信息载体（information carrier）

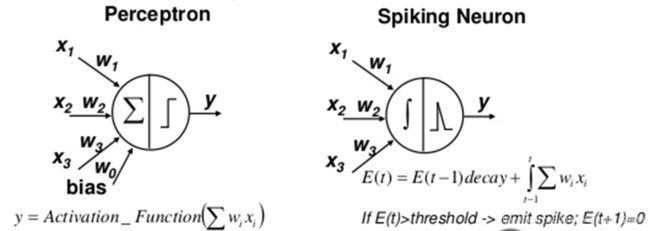
首先， 最基本的区别是SNN和ANN的信息载体不一样。 ANN 使用的是高精度浮点数而SNN使用的是spikes 或可以理解为1和0，这就大大增加了信息在网络中的稀疏性。这些spike在网络中有相同的幅度和duration.

图1左：传统神经网络结构。 右：SNN结构

那么，在SNN中， 信息是如何用spike来表达的呢？ 这就涉及到脉冲编码的知识了。这里做简单介绍，之后我会再详细解释它。 在SNN中， 很重要的一点是引入了时序（temporal）相关的处理形式。 信息是被编码在脉冲序列的时间序列（spike train）中的。 例如： 高频率的一组脉冲序列可以代表一个较高的值而低频率的脉冲则代表低值。又例如： 在一个固定的时间窗中， 单个脉冲出现的位置也可以代表相应的值/信息。

2，神经元

图2左：传统神经元。 右：spiking neuron

既然信息的载体不一样， 那么神经网络中的基本单元–神经元肯定也是不一样的。 对ANN有了解的同学们都知道， 基本神经元perceptron 是一个简单的 加乘运算器用来整合输入该神经元的值 而后接着一个非线性的激活方程（Non-linear activation function）。然而这种针对确切数值的运算并不适用于二进制脉冲的处理。 在SNN中， 基本的运算单元为以生物突触结构为基础构建的脉冲神经元（spiking neuron)。 想象有两个spiking neuron 其中一个为突触前神经元（pre-synaptic neuron）作为spiking的发出者， 一个为突触后神经元（post-synaptic neuron) 作为spike的接受者。 spiking neuron所进行的处理是接受由突触传递而来的脉冲， 依据突触权重通过spiking function产生突触后膜电压（post synaptic potential (PSP)）

图2 spiking neuron的示例。 PSP代表post synaptic potential.

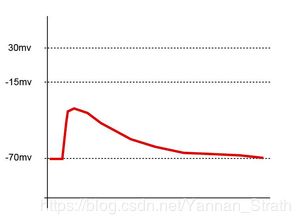
那么PSP是什么呢？ 简单的解释就是神经元上的膜电压变化。例如图三就是一个神经元接受到spike后膜电压 $u(t)$随着时间 $t$ 的变化。在生物学中， 这种电脉冲的幅值和时间常数是在特定范围内的， 例如图三中， 膜电压在接受到脉冲输入前会一直保持在 $-70$mV 的地方， 这个值通常叫做静止值（resting value）。 当接受到刺激后， 会产生电压变化的幅值。 在变化结束后， 膜电压会归位回起始的静止值。在实际操作中这种波形要怎样产生呢？ 科学家们对生物神经元进行实验分析后， 给出了许多神经元的差分方程（differential equation）模型:

例如：
IF neuron(integrated and fire)

$I(t)=C_m\frac{d{V}_m(t）}{dt}$

可以看出来式子为电容定律的时间导数，Q = CV。 当施加输入电流时，膜电压会随时间增加，直到达到恒定阈值Vth，此时将出现增量函数尖峰，并且电压会重置为其静止电位，此后模型将继续运行。

除此之外Hodgkin–Huxley 模型， LIF模型， SRM模型等等。 但Neuron model在SNN中的作用主要还是作为脉冲序列的处理单元， 其真正的生物学仿真特性我个人认为在SNN的实际应用过程中不必要求过于苛刻的接近于实际生物学的膜电压波形。

图3 单个spike产生的膜电压变化。

那么像图4一样， 当一个突触后神经元接受到多个channel的脉冲序列输入膜电压会发生什么样的变化呢？

图4 单个spiking neuron接受多个spike输入。

图5 膜电压变化仿真。

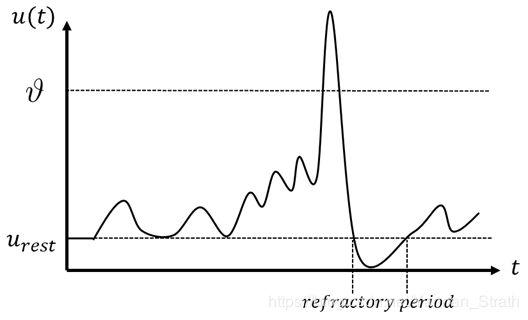
如图5所示。 突触后神经元会首先按照接受到的时间整合脉冲， 将他们变为膜电压的变化的叠加。 当膜电压超过预先设置好的阈值（$\vartheta$）时，突触后neuron被认定为收到了足够的刺激从而发出一个脉冲（spike）。 在发出脉冲后， 膜电压会被重置并且突触后神经元会在一段时间内无法处理接收到的脉冲， 这段时间称为神经元的refractory period。 在refractory period之后， 膜电压会恢复到静止值从而可以准备下一次脉冲的产生。 这就是脉冲神经元一次完整的spike generation过程。

3，学习方法/使用方法

传统ANN主要依赖于基于梯度下降的反向传播算法。 但在SNN中， 因为spiking neuron的function通常为不可导的差分方程， 在SNN中实现反向传播就显得异常的困难。 那么如何训练SNN呢？在实际应用N中， SNN implementation主流的方式大概有三种， 这里做简要的方法叙述：

1. 将传统ANN转换为SNN
   既然SNN不可以使用BP来训练那么将传统的神经网络训练好转换为SNN是有可能的吗？ 答案是肯定的。 这种方法的优点是不用考虑任何SNN的特性， 但要将训练好的网络在输入，运算和输出上全面转换为以二进制spike为处理载体的网络。 在输入上，要将输入信号编码为脉冲序列。 所有神经元要用相应的spiking neuron来替换， 训练所得得权重要进行量化。

2. 反向传播

欸，作者。你不是刚刚提到SNN得spike function是无法进行反向传播得嘛？那为啥这里又说它可以了？ 没错， 脉冲神经元得spike function的确无法直接求导做差计算出梯度。 但研究人员想出了很多聪明得方法来预估网络中得变化参数得梯度从而进行反向传播。 这样得算法虽然还存在争论但它确实在某种程度上降低了SNN得训练复杂度， 这样得算法比如有 spikeprop, Slayer 等等

3. 突触可塑性

这个相比前两种方法就更加接近于生物学得学习了。 利用生物学得原理研究人员将spike time dependent plasticity （脉冲时间相关可塑性）引入了SNN得训练。 然而这种训练方法虽然novel， 但训练过程非常繁琐， 而且是一种纯非监督式学习， 非常考验设计者对神经科学和神经网络得理解， 我会后续继续写出相关得博客来介绍并使用它。

ANN VS SNN

总结， SNN目前仍在快速发展中， 其优势展现在于相比ANN具有更大的移动设备应用潜能。 这主要归于它的处理方式可以结合新型的类脑芯片（neuromorphic chips）实现高速低功耗的大规模网络运算。

写在最后

第一次撰写个人博客， 所想所写都仅为个人理解， 如有错误欢迎指出和更正。 期待与您共同在新兴领域进行探索和学习。

在后续博客中，我准备继续更新以下内容：

1. SNN的发展现状以及已经出现的应用
2. 类脑传感器：动态视觉传感器Dynamic sensor和人工耳蜗：silicon cohlear
3. 实例教学：基于SNN的手写数字识别
4. 实例教学：基于卷积脉冲神经网络的物体识别
5. 实例教学：基于脉冲神经网络的动态手势识别