BPSK、QPSK、16QAM、64QAM到底是个啥

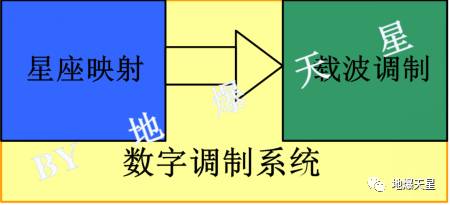
聊一聊数字调制，一般可以认为数字调制比模拟调制多了一个程序，就是星座映射。在星座映射之前，信源编码之后，有时候还会有纠错码的环节，某些情况还不止一个纠错码，为了方便这里先略去不表。

 

数字调制系统组成

 

星座映射和载波调制这两个部分并非独立存在的，相反这两者结合的非常紧密，甚至可以说是互为依靠并不过分。

 

那末，星座映射也就要根据调制载波的方式来进行了，于是也就很好想了，大致上分为三类。

 

I  振幅键控（ASK，amplify shift keying）

 

小星君一直觉得这个名字里的“键”字比较传神，ASK也叫脉冲幅度调制（PAM）。通俗说ASK就是AM，区别就在于模拟和数字之间的关键性区别，就是前边小星君讲过的模拟信号连续而数字信号不连续。下边简单回顾一下模拟/数字信号。

 

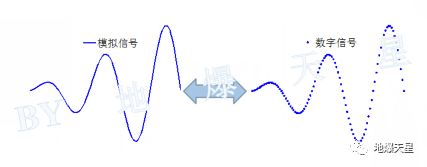
模拟信号和数字信号再次对比

 

如图所示，左侧表示模拟信号，在时间和幅度两个方向，都是连续取值的。右侧表示数字信号，从时间上看是一个个离散时刻的点；从幅度上看，每个点的值实际上都量化取值。

 

量化是一个接收端概念，数字器件的处理精度是有限的，比如8比特只能表示0到255这一共256个整数，如果某个量的原始值是127.2356，机器是无法表示那么精确的，只能就近四舍五入取值127，这就是量化。

 

回到ASK，星座映射是在发射端完成的，不涉及量化问题。由信源编码得到的01比特信息，就是把照片或者mp3或者视频变成的01序列，又或者是更进一步，对这个01比特信息进行信道纠错编码后得到的01比特信息，要将这个序列按照每m个比特打包时，一共可以取2^m个不同的值。

 

这里与量化有些类似，要想办法把01序列映射成与之对应的整数值。举个例子，要把每3个比特打包，那么3个01的不同组合一共有8种，所以整数值分别取-7, -5,-3,-1,1,3,5,7。那么关键的问题就是，如何将01和这8个整数对应起来？

 

星座映射就是完成把01变成整数这个功能，这里的映射有函数的思想，具体如何映射可以自由定义。比如：000映射为整数-7，001映射为整数-5，…，111映射为整数7。当然，把000映射为7，111映射为-7，也是完全可以的。需要注意的是，在发射端怎样映射的，在收端就要按照这个规则反映射。不能在发端把000映射为7，到了终端却把收到的7反映射为111。

 

8进制的ASK调制

 

OK，当已经确定了调制进制时，把01比特映射为多进制的整数，就完成了ASK。

 

最后回到星座映射，这个名词除了映射还有星座的概念。小星君一直觉得星座应该是取自于星空，当我们把01序列映射为一个个具有整数概念的点时，就像是把01打包挂到天空中一个个星星上。这就有一个小小尴尬，星空我们认为是二维的，而ASK却是站在一维角度（幅度轴），所以习惯上，通信一般不把星座映射这个概念放在幅度键控这里。

 

那么，星座映射一定是用于二维映射了，有哪些呢？

 

 

II 相移键控PSK

 

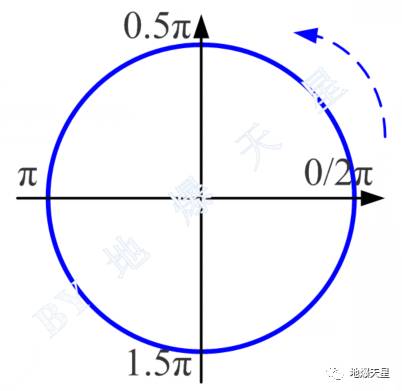
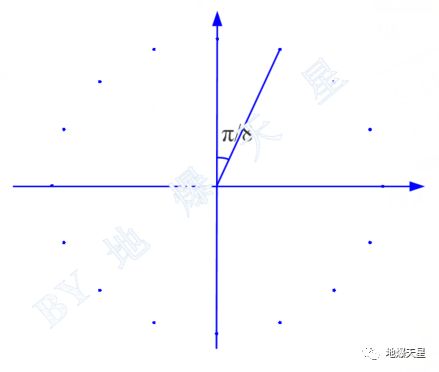
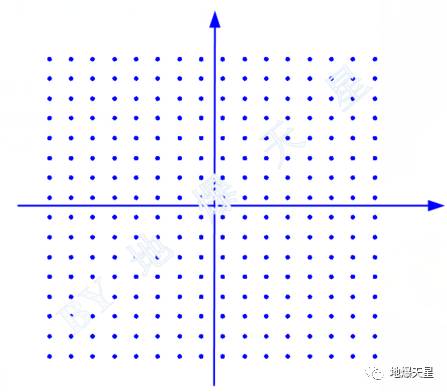
我们都知道，三角函数的相位变化范围在0到2π，放在单位圆里，相位为0和2π的点重叠于x轴正半轴，相位为0.5π、π、1.5π三个点分别在y轴正半轴、x轴负半轴、y轴负半轴。

 

图1 单位圆，相位逆时针增加

 

PSK就平均分割整个0到2π的相位，简单的说也就是在单位圆上-等-间-隔-取点。取多少个点，就看调制进制了。比如2进制，就是所谓的BPSK，在单位圆上取两个点。而4进制的QPSK，就是取四个点。

 

 

---

是不是一定要等间隔这么样操作？并非必须。但是考虑到抗噪声和抗干扰能力，最好是尽量让调制的星座点之间距离最大。对于单位圆，怎么样才能距离最大？自然是等间隔了。

 

---

 

二进制相位调制取得的两个点都在x轴上，很容易联想到幅度调制ASK的一个特殊情况，2ASK也是把0和1映射为两种幅度值比如正负1，那么二者在传输方面的性能是否一样呢？这个问题请持续关注地爆天星公众号，小星君会在后续分解“各种调制方式的性能”中结合计算机仿真给出确切答案。

 

回到星座映射，沿着单位圆将整个圆弧进行等分，假设进制为M，那么任意两个相邻星座点与圆心连线之间的夹角就能算出来，是2π/M。下边分别画出8PSK和16PSK的星座图。

 

8PSK星座图

 

16PSK星座图

 

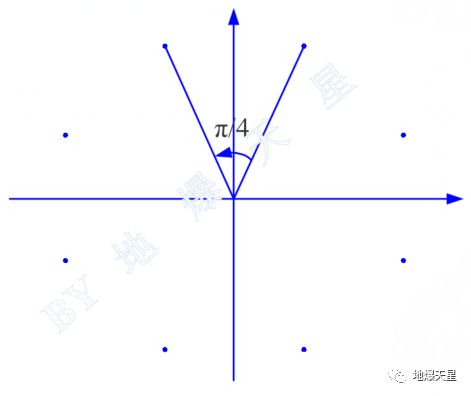
对比8进制和16进制，显而易见进制越高星座点也就相对越密集，因为单位圆总共就只有那么大，分的越多自然只能越密集了。虽然各星座点的密集程度受限于进制数，但是它们的位置却可以相对自由一些，只要保证各相邻点与圆心的夹角不变，整体相对旋转一个初始相偏是不会影响性能的。如下图。

 

有π/8 初始相偏的8PSK星座图

 

PSK星座点分布在单位圆上，在幅度方面完全没有差异。所以对于调相信号，不必考虑幅度方面带来的影响，凡事有利必有弊，这里的星座点也是一样。忽略了幅度信息，就好比拿一张纸表示整个二维平面，在纸上画个圆，然后只单独使用这个圆，而整张纸的绝大部分都浪费了。

 

于是，既使用相位信息，又使用幅度信息的正交幅度调制就吸引了关注。

 

III 正交幅度调制QAM

 

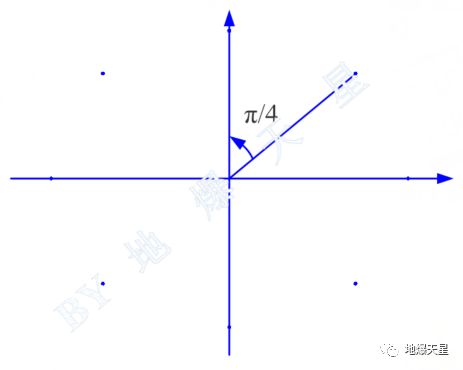
这种算法同时调整幅度和相位，它需要通过两个正交波形来完成，从这个角度稍微难理解一些，小星觉得把这种调制表达成A*exp(jθ)，就方便理解多了，A表示幅度，θ表示相位。

 

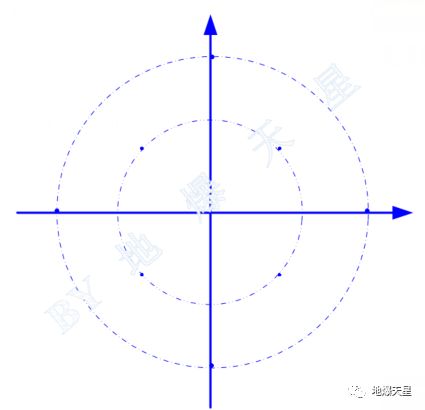
通过后者可以得到一种更加具有辨识性的判断方法，把QAM看作ASK和PSK的级联。比如8进制的QAM，看作2进制ASK级联4进制PSK。通俗的说就是两种幅度，每种幅度有四个相位。如下图的样子

 

8QAM：两个圆表示2ASK，每个圆上四个星座点表示4PSK

 

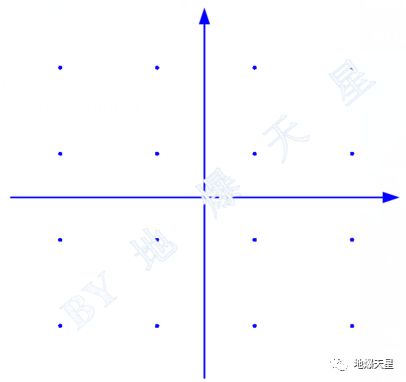
考虑到能尽量分散的把各个星座点分布，提高抗噪声能力，一般QAM把星座点安排成为矩形分布。比如这样的16QAM和256QAM星座图。

 

16QAM星座图 

 

256QAM星座图

 

IV 有记忆调制

 

ASK、PSK还有QAM这三种调制都是无记忆的，这样的调制器在时间上靠前的调制信号与靠后的调制信号完全没有关联，比较容易实现。

 

还有一类调制方式必须以正交波形的形式出现，信号在时间上前后有强的关联，称之为有记忆调制。