K均值聚类算法(Kmeans)讲解及源码实现

K均值聚类算法(Kmeans)讲解及源码实现

---

算法核心

K均值聚类的核心目标是将给定的数据集划分成K个簇，并给出每个数据对应的簇中心点。算法的具体步骤描述如下。

1. 数据预处理，如归一化、离群点处理等。
2. 随机选取K个簇中心，记为${\mu }_1^{(0)},{\mu }_2^{(0)},...,{\mu }_k^{(0)}$。
3. 定义代价函数：$J(c,\mu )=mi{n}_{\mu }mi{n}_c{\Sigma }_{i=1}^M||x_i-{\mu }_{c_i}|{|}^2$。
4. 令$t=0,1,2,...$为迭代步数，重复下面过程直到$J$收敛

• 对于每一个样本$x_i$，将其分配到距离最近的簇$$c_i^{(t)}\leftarrow argmi{n}_k||x_i-{\mu }_k^{(t)}|{|}^2$$
• 对于每一个类簇$k$，重新计算该类簇的中心$${\mu }_k^{(t+1)}\leftarrow argmi{n}_{\mu }{\Sigma }_{i:x_i^{(t)}=k}||x_i-\mu |{|}^2$$

$K$均值算法在迭代时，假设当前损失函数$J$没有达到最小值，那么首先固定簇中心$\{{\mu }_k\}$，调整每个样例$x_i$所属的类别$c_i$来让$J$函数减少；
然后固定$\{c_i\}$，调整簇中心$\{{\mu }_k\}$使$J$减少。
这两个过程交替循环，$J$单调递减：当$J$递减到最小值时，${\mu }_k$和$c_i$也同时收敛。

源码实现（含可视化）

导入包

import numpy as np
import matplotlib.pyplot as plt

数据预处理

设置地图尺寸

# map 100*100
high = 100
width = 100

创建随机数据
每一条数据的格式为$(x坐标,y坐标,类别)$，列表初始化为0，类别序数间隔1递增

data = np.random.rand(100, 2)
data = data * [high, width]
data = np.hstack((data, np.zeros([100, 1])))

定义簇数目

# count of classes
classes = 5

定义距离函数，此处我们使用欧氏距离

def distance(point1, center):
    return np.sqrt((point1[0] - center[0]) ** 2 + (point1[1] - center[1]) ** 2)

定义从类别到颜色的映射函数，即
$$类别\ast 255/总类别数$$

def color(i):
    global classes
    return i * 255. / classes

定义主函数

先将plt设置为连续作图模式
然后随机挑选簇中心点，并加入到中心点数组$centers\_data$中

if __name__ == '__main__':
    plt.ion()
    # select center randomly
    centers = np.random.randint(0, 100, [classes])
    centers_data = []
    for i in range(classes):
        data[i][2] = i
        centers_data.append(data[i])

先画散点图，且暂停0.5秒以显示迭代中的聚类情况。

    while True:
        colors = [color(x) for x in data[:, 2]]
        plt.scatter(data[:, 0], data[:, 1], c=colors)
        plt.pause(0.5)

先后依次迭代更新每个点所对应的簇，和每个簇的中心点。

        # caculate nearest center
        for i in range(100):
            distances = np.array([distance(data[i], center_data) for center_data in centers_data])
            i_class = np.argmin(distances)
            data[i][2] = i_class
        # caculate new center
        new_centers_data = np.zeros([classes, 2])
        new_centers_count = np.zeros([classes])
        for j in range(5):
            for i in range(100):
                if data[i][2] == j:
                    new_centers_count[j] += 1
                    new_centers_data[j] += data[i][0:2]

计算五个簇的中心点位置先后变化的最大值，其值小于1e-4（可自定义）时，跳出循环，停止迭代。

		new_centers_data /= np.array([new_centers_count]).T
        dist = np.max([distance(new_centers_data[i], centers_data[i]) for i in range(classes)])
        print('max distance ', dist)
        if dist < 1e-4:
            break

在每次迭代的最后更新中心点数据

		centers_data = new_centers_data

最后关闭连续作图模式，并展示最后的图画，打印结束。

	plt.ioff()
    plt.show()
    print('kmeans completed.')

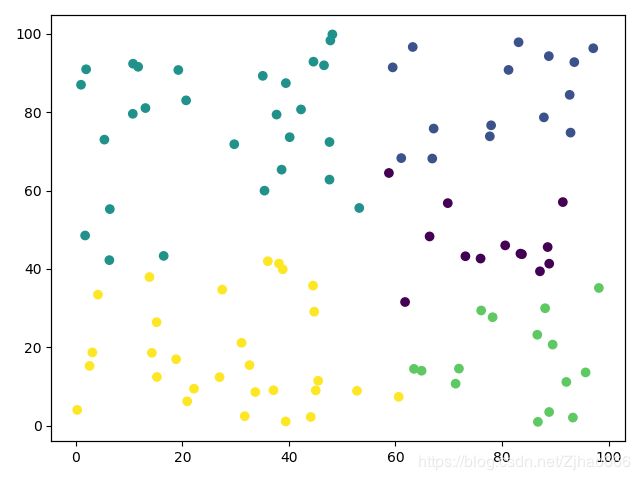
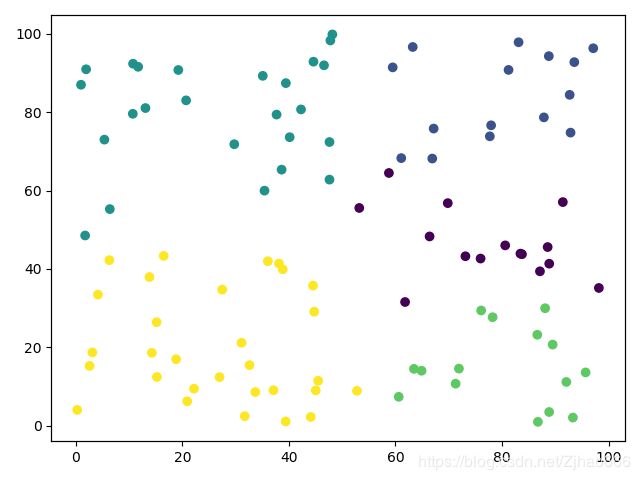
效果

命令行

max distance  28.36595846126929
max distance  7.136259328045152
max distance  3.533885366585787
max distance  2.153654229308223
max distance  0.0
kmeans completed.

可视化过程

第1次迭代

第2次迭代

第3次迭代

第4次迭代

全部代码

import numpy as np
import matplotlib.pyplot as plt

# map 100*100
high = 100
width = 100
# create random data
data = np.random.rand(100, 2)
data = data * [high, width]
data = np.hstack((data, np.zeros([100, 1])))
# count of classes
classes = 5


def distance(point1, center):
    return np.sqrt((point1[0] - center[0]) ** 2 + (point1[1] - center[1]) ** 2)


def color(i):
    global classes
    return i * 255. / classes


if __name__ == '__main__':
    plt.ion()
    # select center randomly
    centers = np.random.randint(0, 100, [classes])
    centers_data = []
    for i in range(classes):
        data[i][2] = i
        centers_data.append(data[i])
    while True:
        colors = [color(x) for x in data[:, 2]]
        plt.scatter(data[:, 0], data[:, 1], c=colors)
        plt.pause(0.5)
        # caculate nearest center
        for i in range(100):
            distances = np.array([distance(data[i], center_data) for center_data in centers_data])
            i_class = np.argmin(distances)
            data[i][2] = i_class
        # caculate new center
        new_centers_data = np.zeros([classes, 2])
        new_centers_count = np.zeros([classes])
        for j in range(5):
            for i in range(100):
                if data[i][2] == j:
                    new_centers_count[j] += 1
                    new_centers_data[j] += data[i][0:2]
        new_centers_data /= np.array([new_centers_count]).T
        dist = np.max([distance(new_centers_data[i], centers_data[i]) for i in range(classes)])
        print('max distance ', dist)
        if dist < 1e-4:
            break
        centers_data = new_centers_data
    plt.ioff()
    plt.show()
    print('kmeans completed.')