KMP是解决两个字符串匹配问题的非常好的算法,算法的时间复杂是O(n)。
现在假设场景是两个字符串str1,str2,求str2是否是str1的子串,如果是,返回第一个子串的第一个字母在str1中的索引。
例如:str1 = "ababcababtk";str2 = "ababtk";则返回5。
要使用KMP算法,首先要算出用来加速匹配的str2的数组next;
一、next数组的求解
next[n]中装的是str2中索引为n的字符前面的子串substr2前缀与后缀相等的最长前缀的长度,前缀与后缀的要求是,前缀一定要包含子串substr2的第一个字符,但是不能包含最后一个字符,后缀一定要包含子串substr2的最后一个字符,但是不能包含最后一个字符。
比如对于字符串str2中的't'前面的子串就是abab,它的前缀是"a","ab","aba";后缀是"b","ab","bab"。前缀与后缀相等的最长前缀的长度是2,所以't'对应的next数组的值是2,即next[4] = 2。
规定next[0] = -1,next[1] = 0,这是人为规定的,当然如果str2的长度为1,那么next数组就只有一个-1。
下面介绍怎么利用前面的next值求后面的next的值。
假设str中n-1位置求出的最长相等前后缀长度是m,要求n位置的最长相等前后缀长度即next[n],下面为了方便表述,将str字符串看成一个str字符数组。
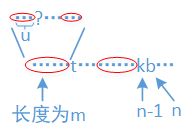
1、str[n-1] = str[m],如下图,n-1和m的位置都是'k',所以'b'对应的next[n] = m+1;
2、str[n-1] != str[m],如下图,则看字符't'对应的next[m],假设next[m] = u,如果next[u]=next[m],则'b'对应的next[n] = u+1,否则再看next[u],按照上述步骤继续进行,直到next[x] = -1为止,此时next[n] = 0;
使用上述方法求出的str2的next数组是[-1,0,0,1,2,0]。
public static int[] getNext(String str){
// 如果str长度为1,直接返回只含-1的数组
if(str.length() == 1){
return new int[]{-1};
}
int[] next = new int[str.length()];
char[] str2 = str.toCharArray();
// 首先将人为设定最长相等前缀的值填好
next[0] = -1;
next[1] = 0;
int n = 2;
// m代表i前面一个字符的最长相等前缀的长度,最开始i=2,next[i-1] = 0,所以n的初始值是0;
int m = 0;
while(n < next.length){
// 这是情况一,str[n-1] = str[m],此时next[n] = m+1
if(str2[m] == str2[n-1]){
next[n++] = ++m;
// 这是情况二,str[n-1] != str[m],此时,m = next[m],再次比较
}else if(m > 0){
m = next[m];
// 当m=0时,则next[n] = 0;
}else{
next[n++] = 0;
}
}
return next;
}
二、使用next数组加速匹配
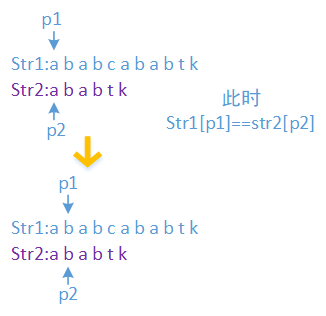
还是上述问题,str1 = "ababcababtk";str2 = "ababtk",上面已经求出str2的next数组是[-1,0,0,1,2,0],p1是指向str1当前匹配位置的指针,p2是指向str2当前位置的指针,开始匹配时会出现下面的情况。为了方便描述,还是将str1和str2看成两个字符数组。
1、str1[p1] == str2[p2] ,则p1和p2都往后移一位。
2、str1[p1] != str2[p2]且p2 != 0,则p2 = next[p2],p1不动。
3、str1[p1] != str2[p2]且p2==0,p2不移动,p1向后移动一位。
如果p2 = str2.length,停止上述过程,此时子串的第一个字符在str1中的位置是p1-p2,否则直到str1遍历完,之后若p2 != str2.length,则str1中不包含str2,否则子串的第一个字符在str1中的位置是p1-p2。
完整代码实现如下:
public static void main(String[] args) {
String str1 = "ababcababtk";
String str2 = "ababtk";
int[] next = getNext(str2);
int res = KMP(str1,str2,next);
System.out.println(res);
}
public static int KMP(String str1,String str2,int[] next){
if(str1 == null || str2 == null || str2.length() < 1 || str1.length() < str2.length()){
return -1;
}
char[] strArr1 = str1.toCharArray();
char[] strArr2 = str2.toCharArray();
int p1 = 0;
int p2 = 0;
while(p1 < strArr1.length && p2 < strArr2.length){
// 情况1,strArr1[p1] == strArr2[p2] ,则p1和p2都往后移一位
if(strArr1[p1] == strArr2[p2]){
p1++;
p2++;
// 情况3,str1[p1] != str2[p2]且p2==0,p2不移动,p1向后移动一位
}else if(p2 == 0){
p1++;
// 情况2,str1[p1] != str2[p2]且p2!=0,则p2 = next[p2],p1不动。
}else{
p2 = next[p2];
}
}
return p2 == strArr2.length ? p1-p2:-1;
}
public static int[] getNext(String str){
// 如果str长度为1,直接返回只含-1的数组
if(str.length() == 1){
return new int[]{-1};
}
int[] next = new int[str.length()];
char[] str2 = str.toCharArray();
// 首先将人为设定最长相等前缀的值填好
next[0] = -1;
next[1] = 0;
int n = 2;
// m代表i前面一个字符的最长相等前缀的长度,最开始i=2,next[i-1] = 0,所以n的初始值是0;
int m = 0;
while(n < next.length){
// 这是情况一,str[n-1] = str[m],此时next[n] = m+1
if(str2[m] == str2[n-1]){
next[n++] = ++m;
// 这是情况二,str[n-1] != str[m],此时,m = next[m],再次比较
}else if(m > 0){
m = next[m];
// 当m=0时,则next[n] = 0;
}else{
next[n++] = 0;
}
}
return next;
}