读书笔记-opencv-阈值分割
读书笔记-opencv-阈值分割
阈值分割处理主要是灰度值信息提取前景,所以对前景物体与背景物体有较强的对比度的图像的分割特别有用,对对比度很弱的图像进行阈值分割,需要先进行对比度增强,在进行阈值处理。常用的两种:全局阈值分割和自适应局部阈值分割。
全局阈值分割
全局阈值分割指的是将灰度值大于thresh(阈值)的图像设为白色,小于或者等于thresh的像素设为黑色;或者反只。
假设输入图像为I,高为H,宽为W,I(r,c)代表第r行第c列的灰度值,0<=r
或者:
O ( r , c ) = { 0 , I ( r , c ) > t h r e s h 255 , I ( r , c ) ≤ t h r e s h O(r,c)= \begin{cases} 0,\quad I(r,c)>thresh \\ 255, I(r,c) \leq thresh\end{cases} O(r,c)={0,I(r,c)>thresh255,I(r,c)≤thresh
src[src>150]= 255
src[src<=150]= 0
图像处理不改变原图,先将原图进行复制,再进行操作,opencv提供threshold()函数:
threshold(InputArray src, OutputArray dst, double thresh, double maxval, int type)
src:单通道矩阵,数据类型为CV_8U或者CV_32F;
dst输出矩阵,即阈值分割后的矩阵; thresh: 阈值
maxVal:在图像二值化显示时,一般设为255
type:类型查看枚举类型ThresholdTypes
enum ThresholdTypes{THRESH_BINARY = 0, THRESH_BINARY_INV = 1,
THRESH_TRUNC = 2, THRESH_TOZERO = 3,
THRESH_TOZERO_INV = 4, THRESH_MASK = 7,
THRESH_OTSU = 8, THRESH_TRIANGLE = 16}
注意类型为THRESH_OSTU或THRESH_TRIANGLE时,输入参数只支持uchar类型,这是thresh也是作为输出参数的,通过Otsu和TRIANGLE算法自动计算出来的,这两种类型和其他类型配合使用,如设置type = THRESH_OSTU + THRESH_BINARY,先利用THRESH_OSTU计算出阈值,才利用THRESH_BINARY进行阈值分割。THRESH_TRIANGLE和后面的直方图阈值处理原理类似,后面会进行介绍这两种算法。
if __name__ == "__main__":
imagePath = "G:\\blog\\OpenCV_picture\\chapter4\\img4.jpg"
src = cv2.imread(imagePath, 0)
#手动设置阈值
thresh = 60
maxVal = 255
#注意这里返回的也是两个值,若是不用ret来接受返回值,会报错
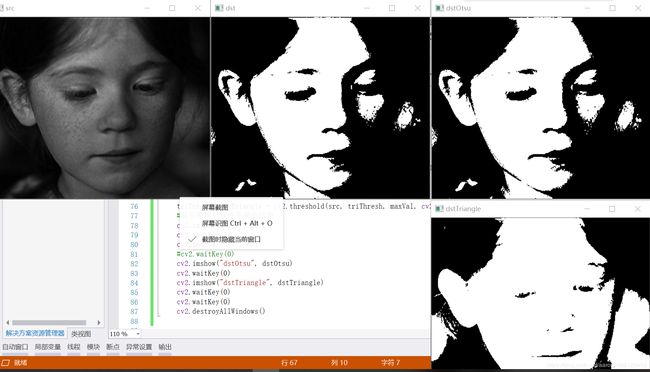
ret, dst = cv2.threshold(src, thresh, maxVal, cv2.THRESH_BINARY)
#THRESH_OTSU和THRESH_TRIANGLE默认和THRESH_BINARY搭配使用
#Otsu阈值处理
otsuThresh = 0
otsuThresh, dstOtsu = cv2.threshold(src, otsuThresh, maxVal, cv2.THRESH_OTSU)
#TRIANGLE阈值处理
triThresh = 0
triThresh, dstTriangle = cv2.threshold(src, triThresh, maxVal, cv2.THRESH_TRIANGLE)
#显示原图和阈值处理后的的图片
cv2.imshow("src", src)
cv2.waitKey(0)
cv2.imshow("dst", dst)
cv2.waitKey(0)
cv2.imshow("dstOtsu", dstOtsu)
cv2.waitKey(0)
cv2.imshow("dstTriangle", dstTriangle)
cv2.waitKey(0)
cv2.destroyAllWindows()
int main()
{
//输入图像
std::string imagePath = "G:\\blog\\OpenCV_picture\\chapter4\\img4.jpg";
Mat src = imread(imagePath, 0);
if (!src.data)
{
std::cout << "load image error!" << std::endl;
return -1;
}
//手动设置阈值
double thresh = 60;
double maxValue = 255;
Mat dst;
threshold(src, dst, thresh, maxValue, THRESH_BINARY);
//Otsu设置阈值
double OtsuThresh = 0.0;
Mat OtsuMat;
OtsuThresh = threshold(src, OtsuMat, OtsuThresh, maxValue, THRESH_OTSU + THRESH_BINARY);
//TRIANGLE设置阈值
double TriThresh = 0.0;
Mat TriMat;
TriThresh = threshold(src, TriMat, TriThresh, maxValue, THRESH_TRIANGLE + THRESH_BINARY);
//显示图像
imshow("src", src);
imshow("dst", dst);
imshow("OtsuMat", OtsuMat);
imshow("TriMat", TriMat);
cout << "OtsuThresh: " << OtsuThresh << " " << "TriThresh: " << OtsuThresh << endl;
waitKey(0);
return 0;
}
运行图片
局部阈值分割
在比较理想的情况下,对整个图像使用单阈值才会成功,在受到光照等其他因素的影响下,全局分割阈值往往不理想,需要局部阈值分割(自适应阈值分割)规则如下:
O ( r , c ) = { 255 , I ( r , c ) > t h r e s h ( r , c ) 0 , I ( r , c ) ≤ t h r e s h ( r , c ) O(r,c) = \begin {cases}255, \quad I(r,c)>thresh(r,c) \\ 0, \quad\quad I(r,c) \leq thresh(r,c) \end{cases} O(r,c)={255,I(r,c)>thresh(r,c)0,I(r,c)≤thresh(r,c)
或者
O ( r , c ) = { 0 , I ( r , c ) > t h r e s h ( r , c ) 255 , I ( r , c ) ≤ t h r e s h ( r , c ) O(r,c) = \begin {cases}0, \quad\quad I(r,c)>thresh(r,c) \\ 255, \quad I(r,c) \leq thresh(r,c) \end{cases} O(r,c)={0,I(r,c)>thresh(r,c)255,I(r,c)≤thresh(r,c)
不像全局阈值只有一个阈值,二十针对每个输入矩阵的元素都有一个阈值,构成相同尺寸的矩阵thresh。
局部阈值分割的核心也是计算阈值矩阵。比较常用的是自适应阈值算法(移动平均值算法)。核心思想是每个像素邻域的“平均值”作为该位置的阈值。
直方图技术法
当一幅图像有一个与背景呈现明显对比的物体的图像会具有包含双峰的直方图,两个峰值对应物体内部和外部较多数目的点两个峰值之间的波谷对应于物体边缘附近相对较少的点。而直方图技术则是根据这一“双峰”特点计算的。首先要找到这两个峰值,然后取两个峰值之间的波谷对应的灰度值,这个灰度值就是阙值,我们采用如下的算法来寻找直方图中的波谷。由于灰度值在直方图中随机波动,在双峰之间可能出现两个较小值,通过鲁棒性选定最小值对应的阈值。一种常见的方式:先对直方图进行高斯平滑,逐渐增大高斯滤波的标准差,知道得到两个直方图的两个唯一波峰和他们之间的最小值。这种需要手动调节,下面介绍的是自动选取波峰和波谷。
假设输入图像为I,高位H,宽为W h i s t o g r a m I histogram_{I} histogramI代表其对应的灰度直方图, h i s t o g r a m I ( k ) histogram_{I}(k) histogramI(k)代表灰度值等于k的像素点个数,其中 0 ≤ k ≤ 255 0\leq k\leq255 0≤k≤255
第一步:找到灰度直方图的第一个峰值,并找到其对应的灰度值也就是该峰值对应的位置,显然,第一个峰值就是灰度直方图的最大值,它对应的灰度值使用firstPeak表示。
第二步:找到灰度直方图的第二个峰值,并找到其对应的灰度值。注意:第二峰值不一定是直方图的第二大值,因为我们需要的峰值是希望在一定邻域内是最大值,如果第二大值和第一大值出现的很近,那么这种情况下第二大值就很明显不是一个峰值。使用如下公式计算最大峰值,
s e c o n d P e a k = a r g k { ( k − f i r s t P e a k ) 2 ∗ h i s t o g r a m I ( k ) } 0 ≤ k ≤ 255 secondPeak=arg_k\{(k-firstPeak)^2*histogram_I(k)\} \quad\quad0\leq k\leq 255 secondPeak=argk{(k−firstPeak)2∗histogramI(k)}0≤k≤255
换成绝对值形式
s e c o n d P e a k = a r g k { ∣ k − f i r s t P e a k ∣ ∗ h i s t o g r a m I ( k ) } 0 ≤ k ≤ 255 secondPeak=arg_k\{|k-firstPeak|*histogram_I(k)\} \quad\quad0\leq k\leq 255 secondPeak=argk{∣k−firstPeak∣∗histogramI(k)}0≤k≤255
第三步:找到两个峰值之间的波谷,如果出现多个波谷,去左侧波谷。波谷计算则取最小值。
c++参考代码
//灰度直方图实现
Mat calGrayHist(const Mat & image)
{
//存储256个灰度级的像素个数
Mat histogray = Mat::zeros(Size(256, 1), CV_32SC1);
//图像的宽和高
int rows = image.rows;
int cols = image.cols;
//计算每个灰度级的个数
for (int i = 0; i < image.rows; i++)
{
for (int j = 0; j < image.cols; j++)
{
int index = int(image.at(i, j));
histogray.at(0, index) += 1;
}
}
return histogray;
}
//直方图阈值分割
int threshTwoPeaks(const Mat & image, Mat & thresh_out)
{
//计算灰度直方图
Mat histogram = calGrayHist(image);
//找到灰度直方图最大峰值对应的灰度值
Point firstPeakLoc;
minMaxLoc(histogram, NULL, NULL, NULL, &firstPeakLoc);
int firstPeak = firstPeakLoc.x;
//寻找灰度直方图第二峰值对应灰度值
Mat measureDists = Mat::zeros(Size(256, 1), CV_32FC1);
for (int k = 0; k < 256; k++)
{
int hist_k = histogram.at(0, k);
measureDists.at(0, k) = pow(float(k - firstPeak), 2)*hist_k;
}
Point secondPeakLoc;
minMaxLoc(histogram, NULL, NULL, NULL, &secondPeakLoc);
int secondPeak = secondPeakLoc.x;
//找到两峰之间最小值作为阈值
Point threshMinLoc;
int thresh = 0;
//
if (firstPeak < secondPeak)
{
minMaxLoc(histogram.colRange(firstPeak, secondPeak), NULL, NULL, &threshMinLoc);
thresh = firstPeak + threshMinLoc.x + 1;
}
else
{
minMaxLoc(histogram.colRange(firstPeak, secondPeak), NULL, NULL, &threshMinLoc);
thresh = secondPeak + threshMinLoc.x + 1;
}
threshold(image, thresh_out, thresh, 255, THRESH_BINARY);
return thresh;
}
int main()
{
//输入图像
std::string imagePath = "G:\\blog\\OpenCV_picture\\第6章\\img7.jpg";
Mat src = imread(imagePath, 0);
if (!src.data)
{
std::cout << "load image error!" << std::endl;
return -1;
}
Mat thresh_out_dst;
int ret = 0;
ret = threshTwoPeaks(src, thresh_out_dst);
if (!ret)
{
cout << "thresh error!" << endl;
return -1;
}
cout << ret << endl;
//显示图片
imshow("src", src);
imshow("dst", thresh_out_dst);
waitKey(0);
return 0;
}
运行结果:
import sys,cv2
import numpy as np
import matplotlib.pyplot as plt
def calcGrayHist(image):
rows,cols = image.shape
grayHist = np.zeros([256],np.uint64)
for r in range(rows):
for c in range(cols):
grayHist[image[r][c]] +=1#把图像灰度值作为索引
return(grayHist)
def threshTwoPeaks(image):
#计算灰度直方图
histogram = calcGrayHist(image)
x_range = range(256)
plt.plot(x_range,histogram,'r',linewidth = 2,c='black')
#设置坐标轴范围
y_maxValue = np.max(histogram)
plt.axis([0,255,0,y_maxValue])
#设置坐标轴标签
plt.xlabel('gray Level')
plt.ylabel('number of pixels')
plt.show()
print(histogram)
print(histogram.shape)
#直方图最大峰值对应的灰度值
maxLoc = np.where(histogram==np.max(histogram))
print(maxLoc)
firstPeak = maxLoc[0][0]
print(firstPeak)
#第二个峰值对应的灰度直方图
measureDists = np.zeros([256],np.float32)
for k in range(256):
measureDists[k] = pow(k-firstPeak,2)*histogram[k]
maxLoc2 = np.where(measureDists==np.max(measureDists))
print(measureDists)
print(maxLoc2)
secondPeak = maxLoc2[0][0]
#找出最小值
thresh = 0
if firstPeak > secondPeak:
temp = histogram[int(secondPeak):int(firstPeak)]
minLoc = np.where(temp ==np.min(temp))
thresh = secondPeak+minLoc[0][0]+1
else:
temp = histogram[int(firstPeak):int(secondPeak)]
minLoc = np.where(temp ==np.min(temp))
thresh = firstPeak+minLoc[0][0]+1
print(temp)
print(minLoc)
threshImage_out = image.copy()
threshImage_out[threshImage_out>thresh]=255
threshImage_out[threshImage_out<=thresh]=0
return(thresh,threshImage_out)
if __name__ =='__main__':
src = cv2.imread('G:/blog/OpenCV_picture/chapter6/img7.jpg',cv2.IMREAD_GRAYSCALE)
re,dst = threshTwoPeaks(src)
print(re)
print(dst)
cv2.imshow('dst',dst)
cv2.waitKey(0)
cv2.destroyAllWindows()
- 运行结果图:
注意:
-
python读取图片的路径设为中文路径,否则会加载错误。
-
直方图技术应用于两个明显波峰有较好的阈值化结果
熵算法
信息熵(entropy)的概念来自信息论,假设信源信号u有n种取值,记为u_{1},u_{2}…u_{n},每一种信号出现的概率记为p_{1},p_{2}…p_{n},那么该信号的信号熵记为: e n t r o p y ( u ) = − ∑ i = 1 n p i log p i entropy(u)=-\sum_{i=1}^{n}p_{i}\log p_{i} entropy(u)=−∑i=1npilogpi,如果把图像看作是一个信源,假设输入图像为I, n o r m a H i s t I normaHist_I normaHistI代表归一化的图像灰度直方图,那么对于8位图,就可以将其看为256个灰度符号,每一个符号出现的概率为 n o r m H i s t I ( k ) normHist_I(k) normHistI(k),
使用熵计算阙值的步骤如下:
第一步:计算归一化的灰度直方图I的累加概率直方图,又称零阶累积矩,记为
c u m u H i s t ( k ) = ∑ i = 0 k n o r m H i s t I ( i ) , k ∈ [ 0 , 255 ] cumuHist(k)=\sum_{i=0}^{k}normHist_I(i),k\in [0,255] cumuHist(k)=i=0∑knormHistI(i),k∈[0,255]
所以,首先要获取灰度直方图,然后将其归一化得到 n o r m H i s t normHist normHist。
第二步:计算各个灰度级的熵,记为
e n t r o p y ( t ) = − ∑ k = 0 t n o r m H i s t I ( k ) log ( n o r m H i s t I ( k ) ) , entropy(t)=-\sum_{k=0}^{t}normHist_{I}(k)\log (normHist_{I}(k)), entropy(t)=−k=0∑tnormHistI(k)log(normHistI(k)),
计算完之后将其存入一个1行256列的矩阵中
第三步:计算使f(t)=f_{1}(t)+f_{2}(t)最大的t的值,即为阙值,其中
f 1 ( t ) = ( e n t r o y ( t ) / e n t r o y ( 255 ) ) ∗ ( l o g ( n o r m H i s t ( t ) ) / l o g { n o r m H i s t ( 0 ) , n o r m H i s t ( 1 ) , . . . , n o r m H i s t ( t ) } ) f 2 ( t ) = ( 1 − e n t r o y ( t ) / e n t r o y ( 255 ) ) ∗ ( l o g ( 1 − n o r m H i s t ( t ) ) / l o g { n o r m H i s t ( t + 1 ) , . . . , n o r m H i s t ( 255 ) } ) f_{1}(t)=(entroy(t)/entroy(255)) * (log(normHist(t))/log\left \{ normHist(0),normHist(1),...,normHist(t) \right \}) \\ \\ f_{2}(t)=(1-entroy(t)/entroy(255)) * (log(1-normHist(t))/log\left \{ normHist(t+1),...,normHist(255) \right \}) f1(t)=(entroy(t)/entroy(255))∗(log(normHist(t))/log{normHist(0),normHist(1),...,normHist(t)})f2(t)=(1−entroy(t)/entroy(255))∗(log(1−normHist(t))/log{normHist(t+1),...,normHist(255)})
代码实现时,要特别注意在第二步和第三步的公式中,log函数要判断参数是否为0,进行相除操作时需要判断被除数是否为0,否则会出现异常。
import cv2
import numpy as np
#from scipy import signal
import math
def calcGrayHist(image):
rows,cols=image.shape
grayHist=np.zeros([256],np.uint64)
for r in range(rows):
for c in range(cols):
grayHist[image[r][c]]+=1
return grayHist
def threshEntroy(image):
rows,cols=image.shape
#灰度直方图
grayHist=calcGrayHist(image)
#归一化直方图即概率直方图
normGrayHist=grayHist/float(rows*cols)
#第一步:计算累加直方图,也称零阶累计矩阵
zeroCumuMoment=np.zeros([256],np.float32)
for k in range(256):
if k==0:
zeroCumuMoment[k]=normGrayHist[k]
else:
zeroCumuMoment[k]=zeroCumuMoment[k-1]+normGrayHist[k]
#第二步:就是那个个灰度级的熵
entropy=np.zeros([256],np.float32)
for k in range(256):
if k==0:
if normGrayHist[k]==0:
entropy[k]=0
else:
entropy[k]=-normGrayHist[k]*math.log10(normGrayHist[k])
else:
if normGrayHist[k]==0:
entropy[k]=entropy[k-1]
else:
entropy[k]=entropy[k-1]-normGrayHist[k]*math.log10(normGrayHist[k])
#找阈值
fT=np.zeros([256],np.float32)
ft1,ft2=0.0,0.0
totalEntroy=entropy[255]
for k in range(255):
maxFront=np.max(zeroCumuMoment[0:k+1])
maxBack=np.max(zeroCumuMoment[k+1:256])
if maxFront==0 or zeroCumuMoment[k]==0 or maxFront==1 or zeroCumuMoment[k]==1 or totalEntroy==0:
ft1=0
else:
ft1=entropy[k]/totalEntroy*(math.log10(zeroCumuMoment[k])/math.log10(maxFront))
if maxBack==0 or 1-zeroCumuMoment[k]==0 or maxBack==1 or 1-zeroCumuMoment[k]==1:
ft2=0
else:
if totalEntroy==0:
ft2=math.log10(1-zeroCumuMoment[k])/math.log10(maxBack)
else:
ft2=(1-entropy[k]/totalEntroy)*(math.log10(1-zeroCumuMoment[k])/math.log10(maxBack))
fT[k]=ft1+ft2
threshLoc=np.where(fT==np.max(fT))
thresh=threshLoc[0][0]
#阈值处理
threshold=np.copy(image)
threshold[threshold>thresh]=255
threshold[threshold<=thresh]=0
return (thresh,threshold)
if __name__ =='__main__':
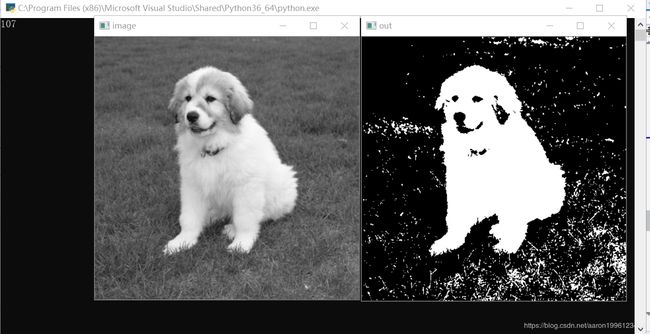
image=cv2.imread("G:\\blog\\OpenCV_picture\\chapter6\\img7.jpg",cv2.IMREAD_GRAYSCALE)
cv2.imshow("image",image)
thresh,out=threshEntroy(image)
print(thresh)
out=np.round(out)
out.astype(np.uint8)
cv2.imshow("out",out)
cv2.waitKey(0)
cv2.destroyAllWindows()
运行结果:
c++实现
//灰度直方图实现
Mat calcGrayHist(const Mat & image)
{
//存储256个灰度级的像素个数
Mat histogray = Mat::zeros(Size(256, 1), CV_32SC1);
//图像的宽和高
int rows = image.rows;
int cols = image.cols;
//计算每个灰度级的个数
for (int i = 0; i < image.rows; i++)
{
for (int j = 0; j < image.cols; j++)
{
int index = int(image.at(i, j));
histogray.at(0, index) += 1;
}
}
return histogray;
}
//直方图阈值分割
int threshTwoPeaks(const Mat & image, Mat & thresh_out)
{
//计算灰度直方图
Mat histogram = calcGrayHist(image);
//找到灰度直方图最大峰值对应的灰度值
Point firstPeakLoc;
minMaxLoc(histogram, NULL, NULL, NULL, &firstPeakLoc);
int firstPeak = firstPeakLoc.x;
//寻找灰度直方图第二峰值对应灰度值
Mat measureDists = Mat::zeros(Size(256, 1), CV_32FC1);
for (int k = 0; k < 256; k++)
{
int hist_k = histogram.at(0, k);
measureDists.at(0, k) = pow(float(k - firstPeak), 2)*hist_k;
}
Point secondPeakLoc;
minMaxLoc(measureDists, NULL, NULL, NULL, &secondPeakLoc);
int secondPeak = secondPeakLoc.x;
//找到两峰之间最小值作为阈值
Point threshMinLoc;
int thresh = 0;
//
if (firstPeak < secondPeak)
{
minMaxLoc(histogram.colRange(firstPeak, secondPeak), NULL, NULL, &threshMinLoc);
thresh = firstPeak + threshMinLoc.x + 1;
}
else
{
minMaxLoc(histogram.colRange(firstPeak, secondPeak), NULL, NULL, &threshMinLoc);
thresh = secondPeak + threshMinLoc.x + 1;
}
threshold(image, thresh_out, thresh, 255, THRESH_BINARY);
return thresh;
}
//熵算法计算全局阙值
int Otsu(const Mat & image, Mat & threshImageOut) {
//获取灰度直方图
Mat histogram = calcGrayHist(image);
//归一化灰度直方图
Mat normHist;
histogram.convertTo(normHist, CV_32FC1, 1.0 / (image.rows*image.cols), 0.0);
//第一步,计算零阶累积矩阵和一阶累计矩阵
Mat zeroCumuHist = Mat::zeros(Size(256, 1), CV_32FC1);
Mat oneCumuHist = Mat::zeros(Size(256, 1), CV_32FC1);
for (int i = 0; i < 256; i++) {
if (i == 0)
{
zeroCumuHist.at(0, i) = normHist.at(0, 0);
oneCumuHist.at(0, i) = i * normHist.at(0, 0);
}
else
{
zeroCumuHist.at(0, i) = zeroCumuHist.at(0, i - 1) + normHist.at(0, i);
oneCumuHist.at(0, i) = oneCumuHist.at(0, i - 1) + i * normHist.at(0, i);
}
}
//计算类间方差
//第二步,计算各个灰度级的熵
Mat variance = Mat::zeros(Size(256, 1), CV_32FC1);
//
float mean = oneCumuHist.at(0, 255);
for (int i = 0; i < 255; i++) {
if (zeroCumuHist.at(0, i) == 0 || zeroCumuHist.at(0, i) == 1)
{
variance.at(0, i) = 0;
}
else
{
float cofficient = zeroCumuHist.at(0, i)*(1.0 - zeroCumuHist.at(0, i));
variance.at(0, i) = pow(mean*zeroCumuHist.at(0, i) - oneCumuHist.at(0, i), 2.0) / cofficient;
}
}
Point threshLoc;
minMaxLoc(variance, NULL, NULL, NULL, &threshLoc);
//阙值分割操作
threshold(image, threshImageOut, threshLoc.x, 255, THRESH_BINARY);
return threshLoc.x;
}
//熵算法计算全局阙值
int threshByEntroy(const Mat & image, Mat & threshImageOut) {
//获取灰度直方图
Mat histogram = calcGrayHist(image);
//归一化灰度直方图
Mat normHist;
histogram.convertTo(normHist, CV_32FC1, 1.0 / (image.rows*image.cols), 0.0);
//第一步,计算零阶累积矩阵
Mat cumuHist = Mat::zeros(Size(256, 1), CV_32FC1);
for (int i = 0; i < 256; i++) {
if (i == 0)
cumuHist.at(0, i) = normHist.at(0, 0);
else
cumuHist.at(0, i) = cumuHist.at(0, i - 1) + normHist.at(0, i);
}
//第二步,计算各个灰度级的熵
Mat entroyHist = Mat::zeros(Size(256, 1), CV_32FC1);
for (int i = 0; i < 256; i++) {
float normHist_i = normHist.at(0, i);
if (i == 0) {
if (normHist_i == 0)
entroyHist.at(0, i) = 0;
else
entroyHist.at(0, i) = -normHist_i * log10(normHist_i);
}
else {
if (normHist_i == 0)
entroyHist.at(0, i) = entroyHist.at(0, i - 1);
else
entroyHist.at(0, i) = entroyHist.at(0, i - 1) - normHist_i * log10(normHist_i);
}
}
//计算最大的f(t),得到阙值
Mat FHist = Mat::zeros(Size(256, 1), CV_32FC1);
float totalEntroy = entroyHist.at(0, 255);
for (int i = 0; i < 256; i++) {
float cumuHist_i = cumuHist.at(0, i);
double maxVal1;
minMaxLoc(normHist(Rect(0, 0, i + 1, 1)), NULL, &maxVal1);
float f1 = 0;
if (cumuHist_i == 0 || cumuHist_i == 1 || maxVal1 == 0 || maxVal1 == 1 || totalEntroy == 0) {
f1 = 0;
}
else {
f1 = (entroyHist.at(0, i) / totalEntroy)*(log10f(cumuHist_i) / log10f(maxVal1));
}
double maxVal2;
minMaxLoc(normHist(Rect(i + 1, 0, 255 - i, 1)), NULL, &maxVal2);
float f2 = 0;
if (cumuHist_i == 0 || cumuHist_i == 1 || maxVal2 == 0 || maxVal2 == 1) {
f2 = 0;
}
else {
if (totalEntroy == 0) {
f2 = log10f(1 - cumuHist_i) / log10f(maxVal2);
}
else
f2 = (1 - entroyHist.at(0, i) / totalEntroy)*(log10f(1 - cumuHist_i) / log10f(maxVal2));
}
FHist.at(0, i) = f1 + f2;
}
Point threshLoc;
minMaxLoc(FHist, NULL, NULL, NULL, &threshLoc);
//阙值分割操作
threshold(image, threshImageOut, threshLoc.x, 255, THRESH_BINARY);
return threshLoc.x;
}
int main()
{
//输入图像
std::string imagePath = "G:\\blog\\OpenCV_picture\\chapter6\\img7.jpg";
Mat src = imread(imagePath, 0);
if (!src.data)
{
std::cout << "load image error!" << std::endl;
return -1;
}
Mat thresh_out_dst;
int ret = 0;
ret = threshTwoPeaks(src, thresh_out_dst);
if (!ret)
{
return -1;
}
cout << ret << endl;
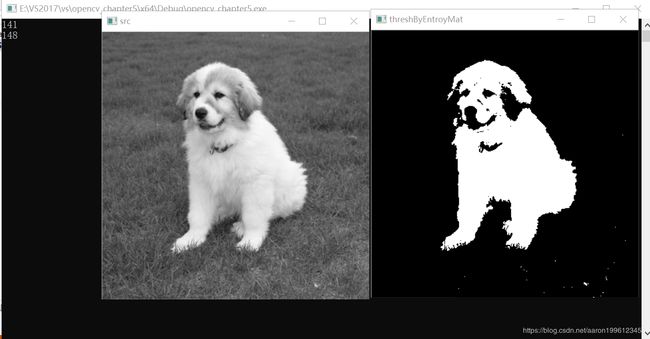
Mat threshByEntroyMat;
ret = threshByEntroy(src, threshByEntroyMat);
if (!ret)
{
return -1;
}
cout << ret << endl;
Mat OtsuMat;
ret = Otsu(src, OtsuMat);
if (!ret)
{
return -1;
}
cout << ret << endl;
//显示图片
imshow("src", src);
imshow("dst", thresh_out_dst);
imshow("threshByEntroy", threshByEntroyMat);
imshow("Otsu", OtsuMat);
waitKey(0);
return 0;
}
Otsu阈值处理
在进行阈值分割时,前景平均阈值和背景平均阈值与整幅图像的平局灰度之间差异最大,Otsu用区域方差表示。
假设输入图像为I,高为H,宽慰W, h i s t g r a m I histgram_I histgramI代表归一化图像的灰度直方图, h i s t g r a m I ( k ) histgram_I(k) histgramI(k)代表灰度值等于k像素个数所占比例, k ∈ [ 0 , 255 ] k\in[0,255] k∈[0,255]:
第一步:计算灰度直方图的零阶累积矩(累加直方图)
z e r o C u m u M o m e n t ( k ) = ∑ i = 0 k h i s t o g r a m I ( i ) , k ∈ [ 0 , 255 ] zeroCumuMoment(k) = \sum_{i=0}^khistogram_I(i),\quad k \in[0,255] zeroCumuMoment(k)=i=0∑khistogramI(i),k∈[0,255]
第二步:计算灰度直方图的一阶累积矩
o n e C u m u M o m e n t ( k ) = ∑ i = 0 k ( i ∗ h i s t o g r a m I ( i ) ) , k ∈ [ 0 , 255 ] oneCumuMoment(k) = \sum_{i=0}^k (i*histogram_I(i)),\quad k \in[0,255] oneCumuMoment(k)=i=0∑k(i∗histogramI(i)),k∈[0,255]
第三步:计算图像I总体的灰度平均值mean,就是k=255时的一阶累加矩
m e a n = o n e C u m u M o m e n t ( 255 ) mean=oneCumuMoment(255) mean=oneCumuMoment(255)
第四步:计算每一个灰度级作为阈值时前景区域的平均灰度,背景区域的平均灰度与整幅图像平均灰度的方差。对方差的衡量采用以下度量
σ 2 = ( m e a n ∗ z e r o C u m u M o m e n t ( k ) − o n e C u m u M o m e n t ( k ) ) 2 z e r o C u m u M o m e n t ( k ) ∗ ( 1 − o n e C u m u M o m e n t ( k ) ) , k ∈ [ 0 , 255 ] \sigma^2 = \frac{(mean*zeroCumuMoment(k) -oneCumuMoment(k))^2}{zeroCumuMoment(k) *(1-oneCumuMoment(k))},\quad k\in[0,255] σ2=zeroCumuMoment(k)∗(1−oneCumuMoment(k))(mean∗zeroCumuMoment(k)−oneCumuMoment(k))2,k∈[0,255]
第五步:找到其中最大的 σ 2 ( k ) \sigma^2(k) σ2(k),然后对应的k即是Otsu自东选区的阈值
t h r e s h = a r g k ∈ [ 0 , 255 ] m a x ( σ 2 ( k ) ) thresh= arg_{k\in[0,255]}max(\sigma^2(k)) thresh=argk∈[0,255]max(σ2(k))
c++实现
//灰度直方图实现
Mat calcGrayHist(const Mat & image)
{
//存储256个灰度级的像素个数
Mat histogray = Mat::zeros(Size(256, 1), CV_32SC1);
//图像的宽和高
int rows = image.rows;
int cols = image.cols;
//计算每个灰度级的个数
for (int i = 0; i < image.rows; i++)
{
for (int j = 0; j < image.cols; j++)
{
int index = int(image.at(i, j));
histogray.at(0, index) += 1;
}
}
return histogray;
}
//直方图阈值分割
int threshTwoPeaks(const Mat & image, Mat & thresh_out)
{
//计算灰度直方图
Mat histogram = calcGrayHist(image);
//找到灰度直方图最大峰值对应的灰度值
Point firstPeakLoc;
minMaxLoc(histogram, NULL, NULL, NULL, &firstPeakLoc);
int firstPeak = firstPeakLoc.x;
//寻找灰度直方图第二峰值对应灰度值
Mat measureDists = Mat::zeros(Size(256, 1), CV_32FC1);
for (int k = 0; k < 256; k++)
{
int hist_k = histogram.at(0, k);
measureDists.at(0, k) = pow(float(k - firstPeak), 2)*hist_k;
}
Point secondPeakLoc;
minMaxLoc(measureDists, NULL, NULL, NULL, &secondPeakLoc);
int secondPeak = secondPeakLoc.x;
//找到两峰之间最小值作为阈值
Point threshMinLoc;
int thresh = 0;
//
if (firstPeak < secondPeak)
{
minMaxLoc(histogram.colRange(firstPeak, secondPeak), NULL, NULL, &threshMinLoc);
thresh = firstPeak + threshMinLoc.x + 1;
}
else
{
minMaxLoc(histogram.colRange(firstPeak, secondPeak), NULL, NULL, &threshMinLoc);
thresh = secondPeak + threshMinLoc.x + 1;
}
threshold(image, thresh_out, thresh, 255, THRESH_BINARY);
return thresh;
}
//熵算法计算全局阙值
int threshByEntroy(const Mat & image, Mat & threshImageOut) {
//获取灰度直方图
Mat histogram = calcGrayHist(image);
//归一化灰度直方图
Mat normHist;
histogram.convertTo(normHist, CV_32FC1, 1.0 / (image.rows*image.cols), 0.0);
//第一步,计算零阶累积矩阵和一阶累计矩阵
Mat zeroCumuHist = Mat::zeros(Size(256, 1), CV_32FC1);
Mat oneCumuHist = Mat::zeros(Size(256, 1), CV_32FC1);
for (int i = 0; i < 256; i++) {
if (i == 0)
{
zeroCumuHist.at(0, i) = normHist.at(0, 0);
oneCumuHist.at(0, i) = i * normHist.at(0, 0);
}
else
{
zeroCumuHist.at(0, i) = zeroCumuHist.at(0, i - 1) + normHist.at(0, i);
oneCumuHist.at(0, i) = oneCumuHist.at(0, i - 1) + i * normHist.at(0, i);
}
}
//计算类间方差
//第二步,计算各个灰度级的熵
Mat variance = Mat::zeros(Size(256, 1), CV_32FC1);
//
float mean = oneCumuHist.at(0, 255);
for (int i = 0; i < 255; i++) {
if (zeroCumuHist.at(0, i) == 0 || zeroCumuHist.at(0, i) == 1)
{
variance.at(0, i) = 0;
}
else
{
float cofficient = zeroCumuHist.at(0, i)*(1.0 - zeroCumuHist.at(0, i));
variance.at(0, i) = pow(mean*zeroCumuHist.at(0, i) - oneCumuHist.at(0, i), 2.0) / cofficient;
}
}
Point threshLoc;
minMaxLoc(variance, NULL, NULL, NULL, &threshLoc);
//阙值分割操作
threshold(image, threshImageOut, threshLoc.x, 255, THRESH_BINARY);
return threshLoc.x;
}
int main()
{
//输入图像
std::string imagePath = "G:\\blog\\OpenCV_picture\\chapter6\\img7.jpg";
Mat src = imread(imagePath, 0);
if (!src.data)
{
std::cout << "load image error!" << std::endl;
return -1;
}
Mat thresh_out_dst;
int ret = 0;
ret = threshTwoPeaks(src, thresh_out_dst);
if (!ret)
{
return -1;
}
cout << ret << endl;
Mat threshByEntroyMat;
ret = threshByEntroy(src, threshByEntroyMat);
cout << ret << endl;
//显示图片
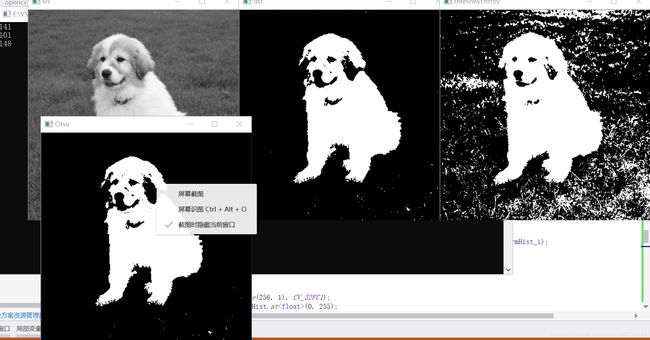
imshow("src", src);
imshow("dst", thresh_out_dst);
imshow("threshByEntroyMat", threshByEntroyMat);
waitKey(0);
return 0;
}
总体上,Otsu处理好于直方图和熵处理,opencv 中提供threshold()函数,其中参数type可以设置为THRESH_OTSU。
自适应阈值
在不均匀照明或者灰度值分布不均匀的情况下,如果使用全局阈值分割,那么得到的分割效果往往不理想。想到的策略是针对每一个位置的灰度值设置一个对应的阈值,而该位置阈值的设置也和其邻域有必然的关系。
在对图像进行平滑处理时,均值平滑、高斯平滑、中值平滑用不同规则计算出以当前像素为中心的邻域内的灰度“平均值”,所以可以使用平滑处理后的输出结果作为每个像素设置阈值的参考值。
在自适应阈值处理中,平滑算子的尺寸决定了分割出来的物体的尺寸,如果滤波器尺寸太小,那么估计出的局部阈值将不理想。凭经验,平滑算子的宽度必须大于被识别物体的宽度,平滑算子的尺寸越大,平滑后的结果越能更好地作为每个像素的阈值的参考,当然也不能无限大。
假设输入图像为I,高为H,宽为W,平滑算子的尺寸记为H*W,其中W和H均为奇数。自适应阈值分割算法的步骤如下:
第一步,对图像进行平滑处理,平滑结果记为 f s m o o t h ( I ) f_{smooth}(I) fsmooth(I),其中 f s m o o t h f_{smooth} fsmooth可以代表均值平滑、高斯平滑、中值平滑。
第二步,自适应阈值矩阵
T h r e s h = ( 1 − r a t i o ) ∗ f s m o o t h ( I ) Thresh=(1-ratio)*f_{smooth}(I) Thresh=(1−ratio)∗fsmooth(I)
,一般令ratio=0.15.
第三步,利用局部阈值分割的规则
在这里插入图片描述
O ( r , c ) = { 255 , I ( r , c ) > T h r e s h ( r , c ) 0 I ( r , c ) ≥ T h r e s h ( r , c ) O(r,c)= \begin{cases}255, \quad I(r,c)>Thresh(r,c) \\0\quad\quad I(r,c)\geq Thresh(r,c) \end{cases} O(r,c)={255,I(r,c)>Thresh(r,c)0I(r,c)≥Thresh(r,c)
或
O ( r , c ) = { 0 , I ( r , c ) > T h r e s h ( r , c ) 255 I ( r , c ) ≥ T h r e s h ( r , c ) O(r,c)= \begin{cases}0, \quad\quad I(r,c)>Thresh(r,c) \\255\quad I(r,c)\geq Thresh(r,c) \end{cases} O(r,c)={0,I(r,c)>Thresh(r,c)255I(r,c)≥Thresh(r,c)
C++实现
在以下c++实现的自适应阈值分割中,利用OpenCV提供的boxfilter、GaussianBlur、medianBlur函数分别完成了均值平滑、高斯平滑和中值平滑,其中radius为平滑算子窗口的半径,即平滑窗口尺寸( 2 ∗ r a d i u s + 1 2*radius+1 2∗radius+1, 2 ∗ r a d i u s + 1 2*radius+1 2∗radius+1),返回值为自适用阈值分割后的结果。具体代码如下
enum METHOD {MEAN,GAUSS,MEDIAN};
Mat adaptiveThresh(Mat I, int radius, float ratio, METHOD method=MEAN)
{
//第一步,对图像矩阵进行平滑处理
Mat smooth;
switch(method)
{
case MEAN://均值平滑
boxFilter(I,smooh,CV_32FC1,Size(2*radius+1,2*radius+1));
break;
case GAUSS:
GaussianBlur(I,smooth,Size(2*radius+1,2*radius+1),0,0);
case MEDIAN:
medianBlur(I,smooth,2*radius+1);
default:
break;
}
//第二步:平滑结果乘以比例系数,然后图像矩阵与其做差
I.convertTo(I,CV_32FC1);
smooth.convertTo(smooth,CV_32FC1);
Mat diff =I-(1.0-ratio)*I_smooth;
//第三步:阈值处理,当大于或等于0时,输出值为255;反之,输出值为0
Mat out = Mat::zeros(diff.size(),CV_8UC1);
for(int r=0;r(r,c)>=0)
{
out.at(r,c)=255;
}
}
return out;
}
OpenCV提供的自适用阈值函数
void adaptiveThreshold(InputArray src,OutputArray dst,double maxValue,int adaptiveMethod,int thresholdType,int blockSize,double C)
//src :单通道矩阵,数据类型为CV_8U
//dst:输出矩阵,即阈值分割后的矩阵
//maxValue:与函数threshold类似,一般取255
//adaptiveMethold:ADAPTIVE_THRESH_MEAN_C:采用均指平滑,ADAPTIVE_THRESH_GAUSSIAN_C:采用高斯平滑
//thresholdType:THRESH_BINARY THRESH_BINARY_INV
//blockSize:平滑算子的尺寸,且为奇数
//C:比例系数
当图像中出现较大的明暗差异时,自适应阈值非常有效。计算每个区域blocksize*blocksize加权平均值(如果选择cv::ADAPTIVE_THRESH_MEAN_C,那么均值时取得权值是相等的;如果选择cv::ADAPTIVE_THRESH_GAUSSIAN_C,(x,y)周围的像素的权值则根据其到中心点的距离通过高斯方程得到)然后减去常数C,结果与对应输入的像素值做比较。
什么是平滑算子,在网上搜索一下,未理解。
一类起光滑作用的算子.给定一个二进小波ψ(x),取重构小波χ(x),使得对于任意w,ψ(2jw)…引进实函数φ(x),使其[傅里叶变换](https://www.baidu.com/s?wd=傅里叶变换&tn=SE_PcZhidaonwhc_ngpagmjz&rsv_dl=gh_pc_zhidao)满足|φ(w)|2=ψ(2jw)χ(2jw),这时2j尺度下的平滑算子定义为其中φ2j(x)=φ…