算法导论学习--红黑树详解之删除(含完整红黑树代码)
前面我们讨论了红黑树的插入的实现,基本思想是分类讨论;然后分情况讨论以后我们发现插入操作调整函数只需要处理三种情况,并不是太复杂。但是删除操作会更复杂一点,因为二叉搜索树的删除操作本身就分成了多种情况,这样在执行删除操作后要处理的情况会更多;下面对于删除操作我们仍旧采取分类讨论的方法,将所有的情况梳理清楚后,就可以理解红黑树的删除调整函数的实质了。
下面先放出红黑树删除函数的代码:
//红黑树删除函数
///类似于二叉树删除函数,不过在删除完成以后需要调用调整函数恢复性质
///总的过程也是按z的左右儿子情况进行分类.
///1.z只有左儿子/右儿子
///2.z有左右儿子,z的后继结点是z的右儿子
///3.z有左右儿子,z的后继结点不是z的右儿子
void RBDelete(RBTree z)
{ ///在下面的过程中y总是指向树中会被删除的结点或是会被替代的结点
///x总是指向要替代z或y的结点
RBTree x=NULL;
RBTree y=z;
int ycolor=y->color; ///记录y原来的颜色
if(z->left==Nul) ///只有右儿子
{
x=z->right;
RBTransplant(z,z->right);
}
else if(z->right==Nul) ///只有左儿子
{
x=z->left;
RBTransplant(z,z->left);
}
else ///左右儿子都有
{
y=RBTreeMinMuM(z->right); ///查找z的后继
ycolor=y->color;
x=y->right; ///因为后面y会被染成z原来的颜色,所以违反性质的就是y的右儿子
if(y->p==z) ///y是z的孩子结点
x->p=y;///这种情况下,y为x的父结点
else ///y不是z的孩子结点的情况
{///先用y的右孩子取代y,然后再更改z的右孩子的指向
RBTransplant(y,y->right);
y->right=z->right;
y->right->p=y;
}
RBTransplant(z,y); ///y取代z
y->left=z->left; ///z的左孩子改变指向
y->left->p=y;
y->color=z->color; ///更改y的颜色,这样的话从y以上红黑树的性质都不会违反
}
///如果y原来的颜色是黑色,那么就意味着有一个黑色结点被覆盖了,
///红黑树的性质可能会被破坏(性质4或5),需要调整
if(ycolor==BLACK)
RBDeleteFixUp(x);
}我们设要删除的结点为z,在下面的过程中y总是指向树中会被删除的结点或是会被替代的结点而x总是指向要替代z或y的结点;从代码上看,红黑树的删除操作与二叉树搜索树一样都是分三种情况进行的:
1).z只有左儿子/右儿子
2).z有左右儿子,z的后继结点是z的右儿子
3).z有左右儿子,z的后继的结点不是z的右儿子
那么现在我们就来分析这三种情况下删除z需要怎样操作,以及删除z后红黑树的那些性质会被违反,我们如何进行调整以恢复性质。
情况1:z只有左儿子/右儿子
这种情况下删除操作是很简单的,我们只需要用z的左孩子或右孩子替代z就行了;然后y表示z,x表示z的左孩子或右孩子,ycolor表示z的颜色。
(1).如果z的颜色为红;那么这种替代以后红黑树不会有任何性质被违反,所以就不需要进行调整。
(2).如果z的颜色为黑;那么就意味着有一个黑色结点被覆盖了,这时如果替代z的x是黑色,那么就意味着黑高减少,性质5被破坏了,这时我们可以在x上再人为的”增添”一重黑色,此时x变成双重黑色的结点,但是性质5恢复了;如果x是红色,那么如果z的父结点是红色的,那么性质4和性质5都就会被破坏,这时我们就可以将x染成红色,这样性质4,性质5都可以恢复了。
情况2:z有左右儿子,并且其右儿子就是其后继结点
我们知道一个结点的后继就是将所有结点按关键字从小到大的排序后,排在其后面的那一个结点。z的右儿子就是z的后继,说明z的右儿子的左子树为空。此时y表示z的右儿子,而x表示y的右儿子。删除过程应该是用x替代y,然后就用y替代z,并且将y染成z原来的颜色,ycolor表示y原来的颜色。现在因为y替代z以后被染成z原来的颜色,所以至z以上红黑树的所有性质都不会变,唯一有可能会影响红黑树性质的地方在x替代y这一点。所以其实情况有返回到情况1了,下面按y的颜色进行分类讨论:
(1).y的颜色为红;那么无论x的颜色为红还是为黑,x替换y以后都不会影响任何性质。
(2).y的颜色为黑;这时与上面的情况1是相似的,如果x为黑,则性质5会被违反,我们通过将其染成双重黑色解决。如果x为红,则性质4,5都会被违反,但是我们可以通过将x染成黑色恢复。
情况3:z有左右儿子,并且z的后继不是其右儿子
其实这种情况和情况2是基本一样的,唯一不同的点在于y的位置会变。在情况2中y是z的右儿子,而在这里我们需要用一个查找后继的函数查找到y,然后x仍然表示y的右儿子,ycolor表示y的颜色。同样的x取代y,然后y取代z并被染成z原来的颜色。所以我们还是只需要关注x取代y的过程。接下来按y的颜色讨论,其实与上面情况2是一模一样的:
(1).如果y的颜色为红色;那么无论x为红还是为黑,替换都不会影响任何性质,无需调整。
(2).y的颜色为黑;如果x为黑,则性质5会被违反,我们通过将其染成双重黑色解决。如果x为红,则性质4,5都会被违反,但是我们可以通过将x染成黑色恢复。
上面的所有情况讨论完了以后,我们就发现如果ycolor为红,则删除以后不需要任何的调整。否则如果ycolor为黑,红黑树的性质就会被违反,需要进入调整函数中调整恢复性质。并且进入调整函数时,如果x为红,那么我们简单的将其染成黑色就可以恢复性质了;如果x为黑,那么进入调整函数是我们就将其看成带有双重黑色的情况,调整函数中需要消除那重额外的黑色。对于x为双重黑色的情况,还有一点需要注意:如果此时x为根结点,我们可以简单的去掉一重黑色就行了(其实就是不需要做任何操作),这时黑高是不会受影响的。所以我们下面集中精力来讨论如何调整双重黑色的情况。
(1).w的颜色为红
此时x的父结点一定是黑色的,我们可以通过将w染成黑色,x的父结点染成红色,然后对x的父结点进行左旋变成下面w为黑的情况(旋转以后要重新指定w)。
(2).w的颜色为黑
此时又需要按照w的左右儿子的颜色进行分类讨论
1).w的左右儿子都为黑色:此时我们可以将w染成红色,x移动为x的父结点,将x在树中上移一层,如果x->p是根结点或x->p原来是红色则结束循环,否则转成情况(1).
2).w的右儿子为黑(左孩子为红):此时我们可以通过染色和选择转成w的右孩子为红的情况(具体的操作见代码)
3).w的右儿子为红:这种情况下,我们是可以通过选择和染色去掉x的双重黑色,结束循环的(具体操作见代码)
至此我们就将调整函数中所有的情况讨论完了,下面给出调整函数的代码:
///红黑树删除调整函数
///这个函数主要要解决的问题是x被染成红黑色,或是双重黑色的问题
///对于第一种情况只要简单的去掉x的红色就行了。
///对于第二种情况我们分情况讨论,将双重黑色的结点在树中上升
///直到转成情况1,或是上升为根结点
void RBDeleteFixUp(RBTree x)
{
while(x!=rt&&x->color==BLACK)
{
if(x==x->p->left)///按x是其父结点的左/右孩子分情况讨论
{///下面的过程要按其兄弟结点的颜色进行分类讨论
RBTree w=x->p->right; ///其兄弟结点
///Case 1
if(w->color==RED)///如果兄弟结点是红色
{///此时父结点一定是黑色;在保证黑高的情况下
///我们通过染色和旋转转成下面兄弟结点为黑色的情况
w->color=BLACK;
x->p->color=RED;
LeftRotate(x->p);
w=x->p->right;
}
///Case 2
if(w->left->color==BLACK&&w->right->color==BLACK)
{///通过染色将x上移一层
w->color=RED;
x=x->p; ///将x在树中上移一层,如果x->p是根结点或x->p原来是红色则结束循环,否则转成情况1
}
else ///情况3,4
{
///Case 3
if(w->right->color==BLACK)
{///染色和右旋成情况4
w->color=RED;
w->left->color=BLACK;
RightRotate(w);
w=x->p->right;
///Case 4
///情况4可以直接结束递归
w->color=w->p->color;
w->p->color=BLACK;
w->right->color=BLACK; ///需要将w的右儿子染成黑色以保证黑高
LeftRotate(x->p);
x=rt;
///break;
}
}
}
else ///处理x是父结点的右儿子的情况
{
RBTree w=x->p->left;
if(w->color==RED)
{
w->p->color=RED;
w->color=BLACK;
RightRotate(x->p);
w=x->p->left;
}
else if(w->left->color==BLACK&&w->right->color==BLACK)
{
w->color=RED;
x=x->p;
}
else
{
if(w->left->color==BLACK)
{
w->right->color=BLACK;
w->color=RED;
LeftRotate(w);
w=x->p->left;
}
w->color=x->p->color;
x->p->color=BLACK;
w->left->color=BLACK;
RightRotate(x->p);
x=rt;
///break
}
}
}
//解决红黑问题
x->color=BLACK;
}下面给出一份带注释和测试数据的完整红黑树代码:
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
#define RED 1
#define BLACK 0
///红黑树结点定义,与普通的二叉树搜索树相比多了一个颜色域
typedef struct node
{
int key,color; ///定义1为红,0为黑
node *p,*left,*right;
node(){
color=BLACK; ///默认结点颜色为黑
}
}*RBTree;
RBTree Nul;///表示空的哨兵结点
RBTree rt; ///表示根结点
///左旋 右旋
///左旋:对具有任意具有右孩子的结点可以进行
///传入要选择的结点指针的引用
///旋转以后x的右孩子y取代了x,而x成为y的左孩子,y的左孩子成为x的右孩子
///下面的代码就是完成这三个部分
void LeftRotate(RBTree x)
{
RBTree y=x->right; ///y表示x的右孩子
x->right=y->left; ///第一步:将x的右孩子设为y的左孩子
if(y->left!=Nul)
y->left->p=x;
y->p=x->p; ///更改y的父结点为x的父结点
if(x->p==Nul) ///第二步:y替代x,需要分情况讨论
rt=y; ///x原来是根结点,则设y为根结点
else if(x==x->p->left)
x->p->left=y; ///更改y为x父结点的左孩子
else
x->p->right=y; ///更改y为x父结点的右孩子
y->left=x; ///第三步:将x设为y的左孩子
x->p=y;
}
///右旋:对任何具有左孩子的结点可以进行
///传入要右旋的结点指针的引用
///旋转以后结点x被左孩子y替换,x成为y的右儿子,y的右孩子成为x的左孩子
void RightRotate(RBTree x)
{
RBTree y=x->left; ///y表示x的左孩子
x->left=y->right; ///第一步:x的左孩子更改为y的右孩子
if(y->right!=Nul)
y->right->p=x;
y->p=x->p; ///更改y的父结点为x的父结点
if(x->p==Nul) ///第二步:y替代x,需要分情况讨论
rt=y; ///x原来为根结点,指定y为新根结点
else if(x==x->p->left)
x->p->left=y; ///更改x父结点的左孩子为y
else
x->p->right=y; ///更改x父结点的右孩子为y
y->right=x; ///第三步:更改y的右结点为x
x->p=y;
}
///红黑树插入调整函数
///我们将插入结点染成红色,可能违反了性质4,所以要进行调整
///调整的过程其实就是根据不同的情况进行分类讨论,不断转换的过程
///最后转成可以通过染色和旋转恢复性质的情况
void RBInsertFixUp(RBTree z)
{
///在下面的代码中z结点总是违反性质4的那个结点
while(z->p->color==RED) ///x是红色,它的父结点也是红色就说明性质4被违反,要持续调整
{
///下面的过程按x->p是其祖父结点的左孩子还是右儿子进行分类讨论
if(z->p==z->p->p->left) ///父结点是其祖父结点的左孩子
{
RBTree y=z->p->p->right; ///表示z的叔结点
///下面按y的颜色进行分类讨论
if(y->color==RED)
{///如果y是红色并z的祖父结点一定是黑色的,这时我们通过下面的染色过程
///在保证黑高不变的情况下(性质5),将z在树中上移两层,z=z->p->p
z->p->color=BLACK;
y->color=BLACK;
z->p->p->color=RED;
z=z->p->p;///如果上移到根节点或某个父结点不为红的结点就可以结束循环了
}
else ///叔结点为黑色
{ ///此时要根据z是其父结点的左孩子还是右孩子进行分类讨论
///如果z是左孩子则可以直接可以通过染色和右旋来恢复性质
///如果z是右孩子则可以先左旋来转成右孩子的情况
if(z==z->p->right)
{
z=z->p;
LeftRotate(z); ///直接左旋
}
///重新染色,再右旋就可以恢复性质
z->p->color=BLACK;
z->p->p->color=RED;
RightRotate(z->p->p);
}
}
else///父结点是祖父结点的右孩子
{
RBTree y=z->p->p->left; ///叔结点
if(y->color==RED)
{
z->p->color=BLACK;
y->color=BLACK;
z->p->p->color=RED;
z=z->p->p;
}
else
{///右儿子的时候可以直接左旋,重新调色恢复性质
///左儿子可以先右旋成右儿子再处理
if(z==z->p->left)
{
z=z->p;
RightRotate(z);
}
z->p->color=BLACK;
z->p->p->color=RED;
LeftRotate(z->p->p);
}
}
}
///将根节点染成黑色,是必要的步骤;处理两种情况
///1.第一次插入根结点被染成红色的情况
///2.和在上面的循环中根节点可能被染成红色的情况
rt->color=BLACK;
}
///红黑树的插入
///RB插入函数与普通的BST的插入函数只是稍微有点不同
///我们将原来的null换成了Nul结点,然后对新加入的结点,染成红色
///然后调用RBInsertFixUp函数进行调整,使得红黑树的性质不被破坏
void RBInsert(int key)
{
RBTree z=new node;
z->color=RED;
z->key=key;
z->p=z->left=z->right=Nul;
RBTree y=Nul;
RBTree x=rt;
while(x!=Nul) ///按照二叉搜索树的性质寻找z的插入点
{
y=x;
if(z->key<x->key)
x=x->left;
else
x=x->right;
}
z->p=y;
if(y==Nul)///插入的是根节点
rt=z;
else if(z->key<y->key)
y->left=z;
else
y->right=z;
RBInsertFixUp(z); ///插入红色结点可能违反了红黑树的某些性质,调用调整函数进行调整
}
///红黑树替换函数,v替换u,与BST的类似
///只负责更改父结点的指向,左右儿子需要自己更改
void RBTransplant(RBTree u,RBTree v)
{
if(u->p==Nul)
rt=v;
else if(u==u->p->left)
u->p->left=v;
else
u->p->right=v;
v->p=u->p;
}
///红黑树后继查找函数
///按二叉搜索树的性质一直往左走
RBTree RBTreeMinMuM(RBTree x)
{
if(x->left==Nul)
return x;
return RBTreeMinMuM(x->left);
}
///红黑树删除调整函数
///这个函数主要要解决的问题是x被染成红黑色,或是双重黑色的问题
///对于第一种情况只要简单的去掉x的红色就行了。
///对于第二种情况我们分情况讨论,将双重黑色的结点在树中上升
///直到转成情况1,或是上升为根结点
void RBDeleteFixUp(RBTree x)
{
while(x!=rt&&x->color==BLACK)
{
if(x==x->p->left)///按x是其父结点的左/右孩子分情况讨论
{///下面的过程要按其兄弟结点的颜色进行分类讨论
RBTree w=x->p->right; ///其兄弟结点
///Case 1
if(w->color==RED)///如果兄弟结点是红色
{///此时父结点一定是黑色;在保证黑高的情况下
///我们通过染色和旋转转成下面兄弟结点为黑色的情况
w->color=BLACK;
x->p->color=RED;
LeftRotate(x->p);
w=x->p->right;
}
///Case 2
if(w->left->color==BLACK&&w->right->color==BLACK)
{///通过染色将x上移一层
w->color=RED;
x=x->p; ///将x在树中上移一层,如果x->p是根结点或x->p原来是红色则结束循环,否则转成情况1
}
else ///情况3,4
{
///Case 3
if(w->right->color==BLACK)
{///染色和右旋成情况4
w->color=RED;
w->left->color=BLACK;
RightRotate(w);
w=x->p->right;
///Case 4
///情况4可以直接结束递归
w->color=w->p->color;
w->p->color=BLACK;
w->right->color=BLACK; ///需要将w的右儿子染成黑色以保证黑高
LeftRotate(x->p);
x=rt;
///break;
}
}
}
else ///处理x是父结点的右儿子的情况
{
RBTree w=x->p->left;
if(w->color==RED)
{
w->p->color=RED;
w->color=BLACK;
RightRotate(x->p);
w=x->p->left;
}
else if(w->left->color==BLACK&&w->right->color==BLACK)
{
w->color=RED;
x=x->p;
}
else
{
if(w->left->color==BLACK)
{
w->right->color=BLACK;
w->color=RED;
LeftRotate(w);
w=x->p->left;
}
w->color=x->p->color;
x->p->color=BLACK;
w->left->color=BLACK;
RightRotate(x->p);
x=rt;
///break
}
}
}
x->color=BLACK;
}
///红黑树删除函数
///类似于二叉树删除函数,不过在删除完成以后需要调用调整函数恢复性质
///总的过程也是按z的左右儿子情况进行分类.
///1.z只有左儿子/右儿子
///2.z有左右儿子,要删除的结点是z的右儿子
///3.z有左右儿子,要删除的结点不是z的右儿子
void RBDelete(RBTree z)
{ ///在下面的过程中y总是指向树中会被删除的结点或是会被替代的结点
///x总是指向要替代z或y的结点
RBTree x=NULL;
RBTree y=z;
int ycolor=y->color; ///记录y原来的颜色
if(z->left==Nul) ///只有右儿子
{
x=z->right;
RBTransplant(z,z->right);
}
else if(z->right==Nul) ///只有左儿子
{
x=z->left;
RBTransplant(z,z->left);
}
else ///左右儿子都有
{
y=RBTreeMinMuM(z->right); ///查找z的后继
ycolor=y->color;
x=y->right; ///因为后面y会被染成z原来的颜色,所以违反性质的就是y的右儿子
if(y->p==z) ///y是z的孩子结点
x->p=y;///这种情况下,y为x的父结点
else ///y不是z的孩子结点的情况
{///先用y的右孩子取代y,然后再更改z的右孩子的指向
RBTransplant(y,y->right);
y->right=z->right;
y->right->p=y;
}
RBTransplant(z,y); ///y取代z
y->left=z->left; ///z的左孩子改变指向
y->left->p=y;
y->color=z->color; ///更改y的颜色,这样的话从y以上红黑树的性质都不会违反
}
///如果y原来的颜色是黑色,那么就意味着有一个黑色结点被覆盖了,
///红黑树的性质可能会被破坏(性质4或5),需要调整
if(ycolor==BLACK)
RBDeleteFixUp(x);
}
///红黑树的中序遍历
void RBInoderSearch(RBTree x)
{
if(x==Nul)
return ;
RBInoderSearch(x->left);
printf("%d ",x->key);
RBInoderSearch(x->right);
}
///通过关键字搜索对应结点
RBTree searchByKey(RBTree x,int k)
{
if(x->key==k)
return x;
if(k<x->key)
return searchByKey(x->left,k);
else
return searchByKey(x->right,k);
return NULL;
}
int main()
{
int a[13]={1,134,21,235,318,12,34,3,99,198};
Nul=new node;
while(1)
{
rt=Nul;
for(int i=0;i<10;i++)
{
RBInsert(a[i]);
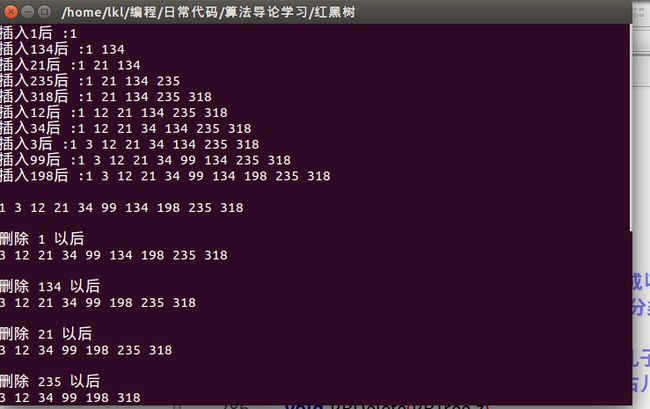
cout<<"插入"<[i]<<"后 :";
RBInoderSearch(rt);
cout<[i]);
RBDelete(x);
cout<<"删除 "<[i]<<" 以后"<