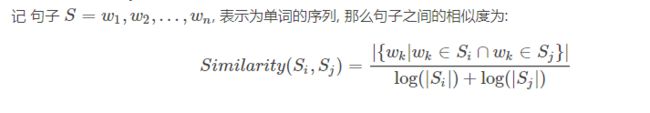NLP句子相似性方法总结及实现
目录
1、基于Word2Vec的余弦相似度
2、TextRank算法中的句子相似性
3、莱文斯坦距离(编辑距离)
4、莱文斯坦比
5、汉明距离
6、Jaro距离(Jaro Distance)
7、Jaro-Winkler距离(Jaro-Winkler Distance)
8、基于Doc2Vec的句子相似度计算
1、基于Word2Vec的余弦相似度
首先对句子分词,使用Gensim的Word2Vec训练词向量,获取每个词对应的词向量,然后将所有的词向量相加求平均,得到句子向量,最后计算两个句子向量的余弦值(余弦相似度)。
余弦相似度:用向量空间中的两个向量夹角的余弦值作为衡量两个个体间差异大小的度量,值越接近1,就说明夹角角度越接近0°,也就是两个向量越相似。
公式:
代码实现:
#对每个句子的所有词向量取均值,来生成一个句子的vector
#sentence是输入的句子,size是词向量维度,w2v_model是训练好的词向量模型
def build_sentence_vector(sentence,size,w2v_model):
vec=np.zeros(size).reshape((1,size))
count=0
for word in sentence:
try:
vec+=w2v_model[word].reshape((1,size))
count+=1
except KeyError:
continue
if count!=0:
vec/=count
return vec
#计算两个句向量的余弦相似性值
def cosine_similarity(vec1, vec2):
a= np.array(vec1)
b= np.array(vec2)
cos1 = np.sum(a * b)
cos21 = np.sqrt(sum(a ** 2))
cos22 = np.sqrt(sum(b ** 2))
cosine_value = cos1 / float(cos21 * cos22)
return cosine_value
#输入两个句子,计算两个句子的余弦相似性
def compute_cosine_similarity(sents_1, sents_2):
size=300
w2v_model=Word2Vec.load('w2v_model.pkl')
vec1=build_sentence_vector(sents_1,size,w2v_model)
vec2=build_sentence_vector(sents_2,size,w2v_model)
similarity = cosine_similarity(vec1, vec2)
return similarity2、TextRank算法中的句子相似性
句子相似性公式:
公式中,Si,Sj分别表示两个句子,Wk表示句子中的词,那么分子部分的意思是同时出现在两个句子中的相同词的个数,分母是对句子中词的个数求对数之和。分母这样设计可以遏制较长的句子在相似度计算上的优势。
代码实现:
def two_sentences_similarity(sents_1, sents_2):
counter = 0
for sent in sents_1:
if sent in sents_2:
counter += 1
sents_similarity=counter/(math.log(len(sents_1))+math.log(len(sents_2)))
return sents_similarity3、莱文斯坦距离(编辑距离)
莱文斯坦距离,又称Levenshtein距离,是编辑距离(edit distance)的一种。是描述由一个字串转化成另一个字串最少的编辑操作次数,其中的操作包括插入、删除和替换。
举例:
- 例如将kitten一字转成sitting:
- sitten(k替换为→s)
- sittin (e替换为→i)
- sitting (添加→g)
- 那么二者的编辑距离为3。
使用python_Levenshtein包进行计算,包下载版本为:python_Levenshtein-0.12.0-cp36-cp36m-win_amd64.whl
然后安装:pip install python_Levenshtein-0.12.0-cp36-cp36m-win_amd64.whl
代码实现:
import Levenshtein
s1='kitten'
s2='sitting'
lev_distance=Levenshtein.distance(s1,s2)
print(lev_distance)4、莱文斯坦比
莱文斯坦比计算公式 r = (sum - ldist) / sum, 其中sum是指str1 和 str2 字串的长度总和,ldist是类编辑距离。
注意:这里的类编辑距离不是3中所说的编辑距离,3中三种操作中每个操作+1,而在此处,删除、插入依然+1,但是替换+2 。这样设计的目的:ratio('a', 'c'),sum=2,按3中计算为(2-1)/2 = 0.5,’a','c'没有重合,显然不合算,但是替换操作+2,就可以解决这个问题。
代码实现:
5、汉明距离
要求str1和str2必须长度一致。是描述两个等长字串之间对应位置上不同字符的个数。
代码实现:
import Levenshtein
s1='abc'
s2='cba'
lev_distance=Levenshtein.hamming(s1,s2)
print(lev_distance)
#结果输出为26、Jaro距离(Jaro Distance)
Jaro Distance 算法是一种计算两个字符串之间相似度的方法。
计算公式:
其中,m为S1和S2的匹配长度(即匹配的字符数),t是换位的数目;如果m=0,则dj=0。
两个分别来自S1和S2的字符如果相距不超过
时,我们就认为这两个字符串是匹配的;而这些相互匹配的字符则决定了换位的数目t,简单来说就是不同顺序的匹配字符的数目的一半即为换位的数目t。
举例:MARTHA与MARHTA的字符都是匹配的,但是这些匹配的字符中,T和H要换位才能把MARTHA变为MARHTA,那么T和H就是不同的顺序的匹配字符,t=2/2=1。那么这两个字符串的Jaro Distance即为:
代码实现:
import Levenshtein
s1='MARTHA'
s2='MARHTA'
lev_distance=Levenshtein.jaro(s1,s2)
print(lev_distance)
#结果输出为0.94447、Jaro-Winkler距离(Jaro-Winkler Distance)
Jaro-Winkler Distance给予了起始部分就相同的字符串更高的分数,他定义了一个前缀p。
计算公式:
其中,dj是两个字符串的Jaro Distance,是前缀的相同的长度,但是规定最大为4,p则是调整分数的常数,规定不能超过0.25,不然可能出现dw大于1的情况,Winkler将这个常数定义为0.1。
举例:6中提及的MARTHA和MARHTA的Jaro-Winkler Distance为:dw = 0.944 + (3 * 0.1(1 − 0.944)) = 0.961
代码实现:
import Levenshtein
s1='MARTHA'
s2='MARHTA'
lev_distance=Levenshtein.jaro_winkler(s1,s2)
print(lev_distance)
#结果输出为0.96118、基于Doc2Vec的句子相似度计算
代码实现:
from gensim.models.doc2vec import Doc2Vec
d2v_model=Doc2Vec.load('data/w2v/doc2vec_model.pkl')
#推断一个句子的向量
sen_vec1=d2v_model.infer_vector('挺 菜品 单一 扇贝 好吃 水果 太少 服务 服务员 服务 挺 开心'.split())
print(sen_vec1)
#返回文档中和sen_vec句子最相似的前top个句子
sen_similar=d2v_model.docvecs.most_similar([sen_vec1],topn=3)
print(sen_similar) #返回的是句子的编号和相似度
结果:
参考:
1、Levenshtein全部函数链接
2、Jaro–Winkler distance链接
3、计算文本相似度工具fuzzywuzzy