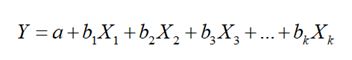Python数据挖掘与机器学习实战——回归分析——线性回归及实例
回归分析
回归分析(Regression Analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法 ,是一种预测性的建模技术。
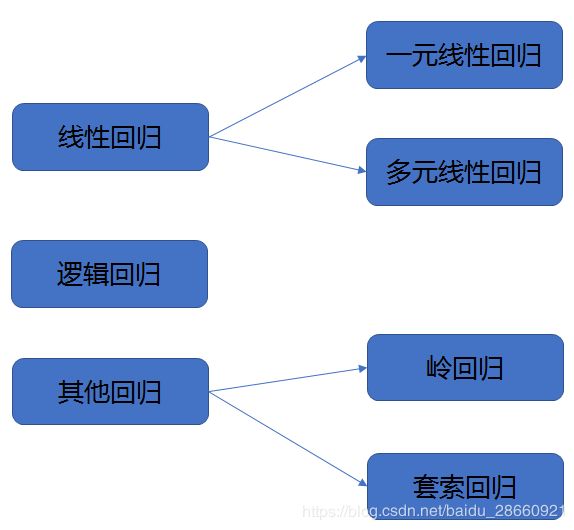
线性回归:
简单而言,就是将输入项分别乘以一些常量,再将结果加起来得到输出。线性回归包括一元线性回归和多元线性回归。
一元线性回归
线型回归分析中,如果仅有一个自变量与一个因变量,且其关系大致上可用一条直线表示,则称之为简单回归分析(一元线性回归)。
如果发现因变量Y和自变量X之间存在高度的正相关,可以确定一条直线的方程,使得所有的数据点尽可能接近这条拟合的直线。简单回归分析的模型可以用以下方程表示:Y=a+bx。其中:Y为因变量,a为截距,b为相关系数,x为自变量。
用python实现一元线性回归:
一个简单的线性回归例子:预测房价,通过房子面积预测房子价值
假设收集到数据如下表:square_feet:平方英尺、price:价格(元/平方英尺)
| square_feet | price | |
| 1 | 150 | 6450 |
| 2 | 200 | 7450 |
| 3 | 250 | 8450 |
| 4 | 300 | 9450 |
| 5 | 350 | 11450 |
| 6 | 400 | 15450 |
| 7 | 600 | 18450 |
(1)在一元线性回归中,必须在数据中找出一种线性关系y(X)=a+bX。
其中y(X)是关于特定平方英尺的价格值(需要预测的值),a是一个常数,b是回归系数
(2)将文件保存为CSV文件,命名为input_data.csv(可以用Excel来做,要加上列名,要和代码.py文件在一个目录下)
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets, linear_model
#读取数据
def get_date(file_name):
data = pd.read_csv(file_name)
X_parameter = []
Y_parameter = []
#遍历数据
for single_square_feet,single_price_feet in zip(data['square_feet'],data['price']):
X_parameter.append([float(single_square_feet)])
Y_parameter.append([float(single_price_feet)])
return X_parameter,Y_parameter
X,Y = get_date('input_data.csv')
print(X)
print(Y)
#输出如下:
[[150.0], [200.0], [250.0], [300.0], [350.0], [400.0], [600.0]]
[[6450.0], [7450.0], [8450.0], [9450.0], [11450.0], [15450.0], [18450.0]](3)把X_parameter,Y_parameter拟合为线性回归模型。需要写一个函数输入X_parameter,Y_parameter和需要进行预测的房子面积值(平方英尺值:square_feet),返回a(常数),b(回归系数)和预测的价格。这里使用scikit-learn机器学习算法。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn import datasets, linear_model
#读取数据
def get_date(file_name):
data = pd.read_csv(file_name)
X_parameter = []
Y_parameter = []
# 遍历数据
for single_square_feet,single_price_feet in zip(data['square_feet'],data['price']):
X_parameter.append([float(single_square_feet)])
Y_parameter.append([float(single_price_feet)])
return X_parameter,Y_parameter
# 将数据拟合到线性模型
def linear_model_main (X_parameter,Y_parameter,predict_value):
# 创建线性回归对象
regr = linear_model.LinearRegression()
regr.fit(X_parameter,Y_parameter) # 用X_parameter,Y_parameter训练模型
predice_outcome = regr.predict(predict_value) # 用predict_value(房屋面积)预测房价
predictions = {}
predictions['intercept'] = regr.intercept_ # 存储a(截距)的值
predictions['coefficient'] = regr.coef_ # 存储b(回归系数)的值
predictions['predicted_value'] = predice_outcome # 存储y(预测的房价)的值
return predictions
X,Y = get_date('input_data.csv')
predictvalue = [[700]] # 书中此处代码是“predictvalue = 700”,但是会报错:ValueError: Expected 2D array, got scalar array instead:
result = linear_model_main(X,Y,predictvalue)
print(result)
print("输出intercept的值:",result['intercept'])
print("输出coefficient的值:",result['coefficient'])
print("输出predicted_value的值:",result['predicted_value'])
# 输出结果如下:
{'intercept': array([1771.80851064]), 'coefficient': array([[28.77659574]]), 'predicted_value': array([[21915.42553191]])}
输出intercept的值: [1771.80851064] # a(截距)
输出coefficient的值: [[28.77659574]] # b(回归系数)
输出predicted_value的值: [[21915.42553191]] # 当房屋面积(x)为700时,预测的房价(y)为21915
# 即模型是y(x)= 1771 + 28 * X(4)为了验证,需要查看数据是否拟合线性回归,所以需要写一个函数,输入X_parameter,Y_parameter,显示数据拟合的直线
#显示线性拟合模型结果
def show_linear_line (X_parameter,Y_parameter):
#创建线性回归对象
regr = linear_model.LinearRegression()
regr.fit(X_parameter, Y_parameter)
plt.scatter(X_parameter, Y_parameter,color='blue')
plt.plot(X_parameter,regr.predict(X_parameter),color='red',linewidth=4)
plt.xticks(())
plt.yticks(())
plt.show()
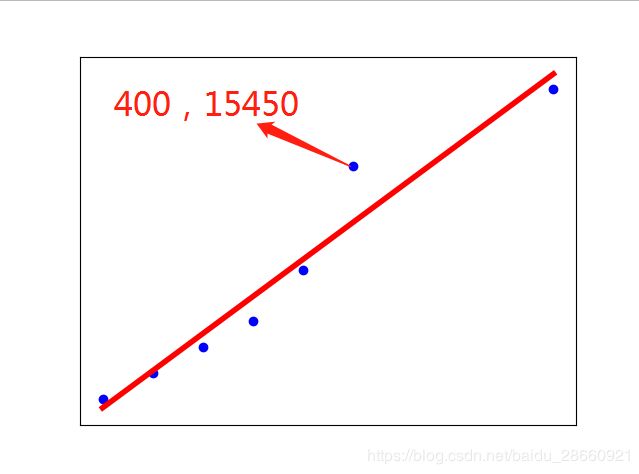
X,Y = get_date('input_data.csv')
show_linear_line(X,Y)从下图可以看出:直线基本可以拟合所有数据点
多元线性回归
多元线性回归是简单线性回归的推广,指的是多个因变量对多个自变量的回归。其中最常用的是只限于一个因变量但有多个自变量的情况,也叫多重回归。多重回归的一般形式如下:a代表截距,b1,b2,...,bk为回归系数。
用python实现多元线性回归
当结果值的影响因素有多个时,可以采用多元线性回归模型
例如:商品销售额可能与电视广告投入、收音机广告投入、报纸广告投入有关系,则:
数据使用Advertising.csv(文末有)
import pandas as pd
data = pd.read_csv('Advertising.csv')
print(data.head()) # 显示前5行数据
print(data.shape) # 显示数据维度
# 输出如下:
TV radio newspaper sales
0 230.1 37.8 69.2 22.1
1 44.5 39.3 45.1 10.4
2 17.2 45.9 69.3 9.3
3 151.5 41.3 58.5 18.5
4 180.8 10.8 58.4 12.9
(200, 4) # 即200行*4列
在这个案例中,通过在电视、广播、报纸上不同的广告投入,预测产品销量。
使用散点图可视化显示特征与响应之间的关系
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# 使用散点图可视化显示特征与响应之间的关系
data = pd.read_csv('Advertising.csv')
# x_vars和y_vars里的内容要和Advertising.csv里的列名完全一样,否则会出现KeyError
sns.pairplot(data,x_vars=['TV','radio','newspaper'],y_vars='sales',size=7,aspect=0.8,kind='reg')
# 通过假如参数kind='reg',seaborn可以添加一条最佳拟合直线和95%的置信带
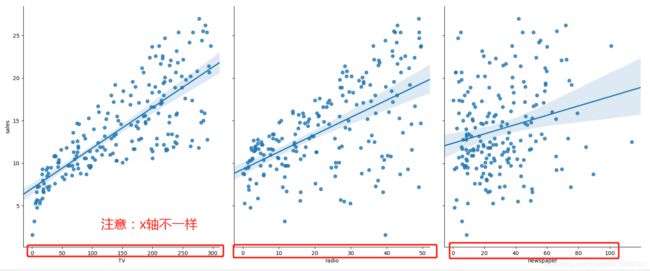
plt.show()运行后得到下图:
x轴都为0-300时,图示应该是这样的
可以看出,销量和TV投入有较强的线性关系,而raido、newspaper和销量的线性关系更弱。
线性回归模型
优点:快速、没有调节参数、可轻易解释、可理解
缺点:相比以他模型,预测准确率不高
(1)使用pandas构建X(特征向量)和y(标签列)
scikit-learn要求X是一个特征矩阵,y是一个Numpy向量,pandas构建在Numpy之上。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv('Advertising.csv')
# 创建特征向量
feature_clos = ['TV','radio','newspaper']
# 使用列表选择原始数据DataFrame的子集
X = data[feature_clos]
X = data[['TV','radio','newspaper']]
# 从DataFrame中选择一个Series
y = data['sales']
y = data.sales
print(X)
print(y)
#输出X如下:
TV radio newspaper
0 230.1 37.8 69.2
1 44.5 39.3 45.1
2 17.2 45.9 69.3
3 151.5 41.3 58.5
4 180.8 10.8 58.4
.. ... ... ...
195 38.2 3.7 13.8
196 94.2 4.9 8.1
197 177.0 9.3 6.4
198 283.6 42.0 66.2
199 232.1 8.6 8.7
[200 rows x 3 columns]
#输出y如下:
0 22.1
1 10.4
2 9.3
3 18.5
4 12.9
...
195 7.6
196 9.7
197 12.8
198 25.5
199 13.4
Name: sales, Length: 200, dtype: float642.构建训练集与测试集
构建训练集与测试集,分别保存在X_train、y_train、X_test、y_test中
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv('Advertising.csv')
# 创建特征向量
feature_clos = ['TV','radio','newspaper']
# 使用列表选择原始数据DataFrame的子集
X = data[feature_clos]
X = data[['TV','radio','newspaper']]
# 从DataFrame中选择一个Series
y = data['sales']
y = data.sales
from sklearn.model_selection import train_test_split
# cross_validation模块在0.18版本中被弃用,现在已经被model_selection代替。
# 所以在导入的时候把"sklearn.cross_validation import train_test_split "
# 更改为"from sklearn.model_selection import train_test_split"
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=1)
# 75%用于训练,25%用于测试
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
# 输出结果如下:
(150, 3)
(50, 3)
(150,)
(50,)3.sklearn的线性回归
使用sklearn做线性回归
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv('Advertising.csv')
# 创建特征向量
feature_clos = ['TV','radio','newspaper']
# 使用列表选择原始数据DataFrame的子集
X = data[feature_clos]
X = data[['TV','radio','newspaper']]
# 从DataFrame中选择一个Series
y = data['sales']
y = data.sales
from sklearn.model_selection import train_test_split
# cross_validation模块在0.18版本中被弃用,现在已经被model_selection代替。
# 所以在导入的时候把"sklearn.cross_validation import train_test_split "
# 更改为"from sklearn.model_selection import train_test_split"
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=1)
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
model = linreg.fit(X_train,y_train) # 线性回归
print(model)
print(linreg.intercept_) # 截距
print(linreg.coef_) # 系数
# 输出结果如下:
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
2.8769666223179335
[0.04656457 0.17915812 0.00345046]所以线性回归结果如下:
y=2.8769666223179335+0.04656457*TV+0.17915812*radio+0.00345046*newspaper
4.预测
通过线性模拟求出回归模型后,可通过模型预测数据,通过predict函数即可求出预测结果
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv('Advertising.csv')
# 创建特征向量
feature_clos = ['TV','radio','newspaper']
# 使用列表选择原始数据DataFrame的子集
X = data[feature_clos]
X = data[['TV','radio','newspaper']]
# 从DataFrame中选择一个Series
y = data['sales']
y = data.sales
from sklearn.model_selection import train_test_split
# cross_validation模块在0.18版本中被弃用,现在已经被model_selection代替。
# 所以在导入的时候把"sklearn.cross_validation import train_test_split "
# 更改为"from sklearn.model_selection import train_test_split"
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=1)
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
model = linreg.fit(X_train,y_train) # 线性回归
y_pred = linreg.predict(X_test)
print(y_pred)
#输出结果如下:
[21.70910292 16.41055243 7.60955058 17.80769552 18.6146359 23.83573998
16.32488681 13.43225536 9.17173403 17.333853 14.44479482 9.83511973
17.18797614 16.73086831 15.05529391 15.61434433 12.42541574 17.17716376
11.08827566 18.00537501 9.28438889 12.98458458 8.79950614 10.42382499
11.3846456 14.98082512 9.78853268 19.39643187 18.18099936 17.12807566
21.54670213 14.69809481 16.24641438 12.32114579 19.92422501 15.32498602
13.88726522 10.03162255 20.93105915 7.44936831 3.64695761 7.22020178
5.9962782 18.43381853 8.39408045 14.08371047 15.02195699 20.35836418
20.57036347 19.60636679]5.评价测度
对于分类问题,评价测度是准确率,但不适用于回归问题,因此使用针对连续数值的评价测度
这里介绍3中常用针对线性回归的评价测度:
平均绝对误差(Mean Absolute Error ,MAE)
即平均绝对值误差,它表示预测值和观测值之间绝对误差的平均值
(绝对误差:测量值与真实值之差)
平均绝对误差MAD=1/(N)*(|x1-xm|+|x2-xm|+..+|xN-xm|)
平均值:xm
![]()
均方误差(mean-square error, MSE)
是指参数估计值与参数真值之差平方的期望值
均方误差可以评价数据的变化程度,MSE的值越小,说明预测模型描述实验数据具有更好的精确度。
均方根误差(Root Mean Square Error,RMSE)
均方根误差是均方误差的算术平方根
案例1:真实值= [2,4,6,8],预测值= [4,6,8,10]
案例2:真实值= [2,4,6,8],预测值= [4,6,8,12]
案例1的MAE = 2.0,RMSE = 2.0
MAE =1/(4)*[|(2-4)|+|(4-6)|+|(6-8)|+|(8-10)|]
RMSE =sqrt{1/(4)*[sqr(2-4)+sqr(4-6)+sqr(6-8)+sqr(8-10)}
案例2的MAE = 2.5,RMSE = 2.65
MAE =1/(4)*[|(2-4)|+|(4-6)|+|(6-8)|+|(8-12)|]
RMSE =sqrt{1/(4)*[sqr(2-4)+sqr(4-6)+sqr(6-8)+sqr(8-12)}
这里使用RMES进行评价测度
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv('Advertising.csv')
# 创建特征向量
feature_clos = ['TV','radio','newspaper']
# 使用列表选择原始数据DataFrame的子集
X = data[feature_clos]
X = data[['TV','radio','newspaper']]
# 从DataFrame中选择一个Series
y = data['sales']
y = data.sales
from sklearn.model_selection import train_test_split
# cross_validation模块在0.18版本中被弃用,现在已经被model_selection代替。
# 所以在导入的时候把"sklearn.cross_validation import train_test_split "
# 更改为"from sklearn.model_selection import train_test_split"
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=1)
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
model = linreg.fit(X_train,y_train) # 线性回归
y_pred = linreg.predict(X_test)
# 计算sales预测的RMSE
from sklearn import metrics
import numpy as np
sum_mean = 0
for i in range(len(y_pred)):
sum_mean += (y_pred[i] - y_test.iloc[i])**2 # 应用y_test.iloc[i]替换y_test.values[i]
sum_erro = np.sqrt(sum_mean/50)
# 输出RMSE
print("输出RMSE:",sum_erro)
# 输出结果如下:
输出RMSE: 1.4046514230328953接下来绘制ROC曲线,代码如下:
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
data = pd.read_csv('Advertising.csv')
# 创建特征向量
feature_clos = ['TV','radio','newspaper']
# 使用列表选择原始数据DataFrame的子集
X = data[feature_clos]
X = data[['TV','radio','newspaper']]
# 从DataFrame中选择一个Series
y = data['sales']
y = data.sales
from sklearn.model_selection import train_test_split
# cross_validation模块在0.18版本中被弃用,现在已经被model_selection代替。
# 所以在导入的时候把"sklearn.cross_validation import train_test_split "
# 更改为"from sklearn.model_selection import train_test_split"
X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=1)
from sklearn.linear_model import LinearRegression
linreg = LinearRegression()
model = linreg.fit(X_train,y_train) # 线性回归
y_pred = linreg.predict(X_test)
# 计算sales预测的RMSE
from sklearn import metrics
import numpy as np
sum_mean = 0
for i in range(len(y_pred)):
sum_mean += (y_pred[i] - y_test.iloc[i])**2 # 应用y_test.iloc[i]替换y_test.values[i]
sum_erro = np.sqrt(sum_mean/50)
import matplotlib.pyplot as plt
plt.figure()
plt.plot(range(len(y_pred)),y_pred,'b',label="predict")
plt.plot(range(len(y_pred)),y_test,'r',label="test")
plt.legend(loc="upper right")
plt.xlabel("the number of sales")
plt.ylabel("value of sales")
plt.show()上面的曲线是真是的曲线,下面的曲线是预测的曲线
至此,一次多元线性回归预测结束
可以看下这个实例:
基于线性回归的股票预测
#附 advertising.csv(数据本身没有第一列(序号),CSV文件里应当删除第一列)
TV,radio,newspaper,sales
1,230.1,37.8,69.2,22.1
2,44.5,39.3,45.1,10.4
3,17.2,45.9,69.3,9.3
4,151.5,41.3,58.5,18.5
5,180.8,10.8,58.4,12.9
6,8.7,48.9,75,7.2
7,57.5,32.8,23.5,11.8
8,120.2,19.6,11.6,13.2
9,8.6,2.1,1,4.8
10,199.8,2.6,21.2,10.6
11,66.1,5.8,24.2,8.6
12,214.7,24,4,17.4
13,23.8,35.1,65.9,9.2
14,97.5,7.6,7.2,9.7
15,204.1,32.9,46,19
16,195.4,47.7,52.9,22.4
17,67.8,36.6,114,12.5
18,281.4,39.6,55.8,24.4
19,69.2,20.5,18.3,11.3
20,147.3,23.9,19.1,14.6
21,218.4,27.7,53.4,18
22,237.4,5.1,23.5,12.5
23,13.2,15.9,49.6,5.6
24,228.3,16.9,26.2,15.5
25,62.3,12.6,18.3,9.7
26,262.9,3.5,19.5,12
27,142.9,29.3,12.6,15
28,240.1,16.7,22.9,15.9
29,248.8,27.1,22.9,18.9
30,70.6,16,40.8,10.5
31,292.9,28.3,43.2,21.4
32,112.9,17.4,38.6,11.9
33,97.2,1.5,30,9.6
34,265.6,20,0.3,17.4
35,95.7,1.4,7.4,9.5
36,290.7,4.1,8.5,12.8
37,266.9,43.8,5,25.4
38,74.7,49.4,45.7,14.7
39,43.1,26.7,35.1,10.1
40,228,37.7,32,21.5
41,202.5,22.3,31.6,16.6
42,177,33.4,38.7,17.1
43,293.6,27.7,1.8,20.7
44,206.9,8.4,26.4,12.9
45,25.1,25.7,43.3,8.5
46,175.1,22.5,31.5,14.9
47,89.7,9.9,35.7,10.6
48,239.9,41.5,18.5,23.2
49,227.2,15.8,49.9,14.8
50,66.9,11.7,36.8,9.7
51,199.8,3.1,34.6,11.4
52,100.4,9.6,3.6,10.7
53,216.4,41.7,39.6,22.6
54,182.6,46.2,58.7,21.2
55,262.7,28.8,15.9,20.2
56,198.9,49.4,60,23.7
57,7.3,28.1,41.4,5.5
58,136.2,19.2,16.6,13.2
59,210.8,49.6,37.7,23.8
60,210.7,29.5,9.3,18.4
61,53.5,2,21.4,8.1
62,261.3,42.7,54.7,24.2
63,239.3,15.5,27.3,15.7
64,102.7,29.6,8.4,14
65,131.1,42.8,28.9,18
66,69,9.3,0.9,9.3
67,31.5,24.6,2.2,9.5
68,139.3,14.5,10.2,13.4
69,237.4,27.5,11,18.9
70,216.8,43.9,27.2,22.3
71,199.1,30.6,38.7,18.3
72,109.8,14.3,31.7,12.4
73,26.8,33,19.3,8.8
74,129.4,5.7,31.3,11
75,213.4,24.6,13.1,17
76,16.9,43.7,89.4,8.7
77,27.5,1.6,20.7,6.9
78,120.5,28.5,14.2,14.2
79,5.4,29.9,9.4,5.3
80,116,7.7,23.1,11
81,76.4,26.7,22.3,11.8
82,239.8,4.1,36.9,12.3
83,75.3,20.3,32.5,11.3
84,68.4,44.5,35.6,13.6
85,213.5,43,33.8,21.7
86,193.2,18.4,65.7,15.2
87,76.3,27.5,16,12
88,110.7,40.6,63.2,16
89,88.3,25.5,73.4,12.9
90,109.8,47.8,51.4,16.7
91,134.3,4.9,9.3,11.2
92,28.6,1.5,33,7.3
93,217.7,33.5,59,19.4
94,250.9,36.5,72.3,22.2
95,107.4,14,10.9,11.5
96,163.3,31.6,52.9,16.9
97,197.6,3.5,5.9,11.7
98,184.9,21,22,15.5
99,289.7,42.3,51.2,25.4
100,135.2,41.7,45.9,17.2
101,222.4,4.3,49.8,11.7
102,296.4,36.3,100.9,23.8
103,280.2,10.1,21.4,14.8
104,187.9,17.2,17.9,14.7
105,238.2,34.3,5.3,20.7
106,137.9,46.4,59,19.2
107,25,11,29.7,7.2
108,90.4,0.3,23.2,8.7
109,13.1,0.4,25.6,5.3
110,255.4,26.9,5.5,19.8
111,225.8,8.2,56.5,13.4
112,241.7,38,23.2,21.8
113,175.7,15.4,2.4,14.1
114,209.6,20.6,10.7,15.9
115,78.2,46.8,34.5,14.6
116,75.1,35,52.7,12.6
117,139.2,14.3,25.6,12.2
118,76.4,0.8,14.8,9.4
119,125.7,36.9,79.2,15.9
120,19.4,16,22.3,6.6
121,141.3,26.8,46.2,15.5
122,18.8,21.7,50.4,7
123,224,2.4,15.6,11.6
124,123.1,34.6,12.4,15.2
125,229.5,32.3,74.2,19.7
126,87.2,11.8,25.9,10.6
127,7.8,38.9,50.6,6.6
128,80.2,0,9.2,8.8
129,220.3,49,3.2,24.7
130,59.6,12,43.1,9.7
131,0.7,39.6,8.7,1.6
132,265.2,2.9,43,12.7
133,8.4,27.2,2.1,5.7
134,219.8,33.5,45.1,19.6
135,36.9,38.6,65.6,10.8
136,48.3,47,8.5,11.6
137,25.6,39,9.3,9.5
138,273.7,28.9,59.7,20.8
139,43,25.9,20.5,9.6
140,184.9,43.9,1.7,20.7
141,73.4,17,12.9,10.9
142,193.7,35.4,75.6,19.2
143,220.5,33.2,37.9,20.1
144,104.6,5.7,34.4,10.4
145,96.2,14.8,38.9,11.4
146,140.3,1.9,9,10.3
147,240.1,7.3,8.7,13.2
148,243.2,49,44.3,25.4
149,38,40.3,11.9,10.9
150,44.7,25.8,20.6,10.1
151,280.7,13.9,37,16.1
152,121,8.4,48.7,11.6
153,197.6,23.3,14.2,16.6
154,171.3,39.7,37.7,19
155,187.8,21.1,9.5,15.6
156,4.1,11.6,5.7,3.2
157,93.9,43.5,50.5,15.3
158,149.8,1.3,24.3,10.1
159,11.7,36.9,45.2,7.3
160,131.7,18.4,34.6,12.9
161,172.5,18.1,30.7,14.4
162,85.7,35.8,49.3,13.3
163,188.4,18.1,25.6,14.9
164,163.5,36.8,7.4,18
165,117.2,14.7,5.4,11.9
166,234.5,3.4,84.8,11.9
167,17.9,37.6,21.6,8
168,206.8,5.2,19.4,12.2
169,215.4,23.6,57.6,17.1
170,284.3,10.6,6.4,15
171,50,11.6,18.4,8.4
172,164.5,20.9,47.4,14.5
173,19.6,20.1,17,7.6
174,168.4,7.1,12.8,11.7
175,222.4,3.4,13.1,11.5
176,276.9,48.9,41.8,27
177,248.4,30.2,20.3,20.2
178,170.2,7.8,35.2,11.7
179,276.7,2.3,23.7,11.8
180,165.6,10,17.6,12.6
181,156.6,2.6,8.3,10.5
182,218.5,5.4,27.4,12.2
183,56.2,5.7,29.7,8.7
184,287.6,43,71.8,26.2
185,253.8,21.3,30,17.6
186,205,45.1,19.6,22.6
187,139.5,2.1,26.6,10.3
188,191.1,28.7,18.2,17.3
189,286,13.9,3.7,15.9
190,18.7,12.1,23.4,6.7
191,39.5,41.1,5.8,10.8
192,75.5,10.8,6,9.9
193,17.2,4.1,31.6,5.9
194,166.8,42,3.6,19.6
195,149.7,35.6,6,17.3
196,38.2,3.7,13.8,7.6
197,94.2,4.9,8.1,9.7
198,177,9.3,6.4,12.8
199,283.6,42,66.2,25.5
200,232.1,8.6,8.7,13.4