深度卷积模型：案例研究

1 经典卷积网络模型

了解一些经典的网络模型，阅读这些论文中的观点可能会对自己很有帮助。LeNet-5、AlexNet、VGG网络，这些都是早期很高效的神经网络，其有些观点成为了现代计算机视觉的基石。除此之外，ResNet，或被称为卷积残差网络，它将网络深度增加至 152 层的同时还提高了训练速度与准确率。Inception 改变了传统 CNN 的结构，可以算是CNN 发展史上的里程碑。

看到这些神经网络后，我们可能有更好的直觉去构建高效的卷积神经网络。

1.1 早期的经典模型

1.1.1 LeNet-5

论文原文：《Gradient-Based Learning Applied to Document Recognition》

网络结构：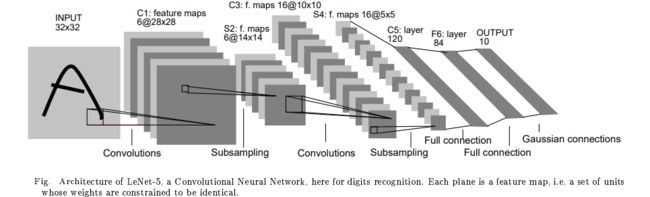
整个模型共 7 层，其中 2 个卷积层，2 个下采样（池化）层，最后 3 个全连接层。大概 60K 个参数。

总结出两个沿用至今的规律：
1、随着层数的加深，特征图的高和宽（大小）越来越小，而其通道数（深度）却越来越深。
2、层的组合为 Conv → pool → Conv → pool → . . . → Fc → Fc → output.

但也有一些与现在不同的地方：
1、隐藏层采用 sigmoid 或 tanh 函数，而现在一般用 relu 函数。
2、输出层采用的是别的分类器，而现在一般用 softmax。

1.1.2 AlexNet

论文原文：《ImageNet Classification with Deep Convolutional Neural Networks》

网络结构：

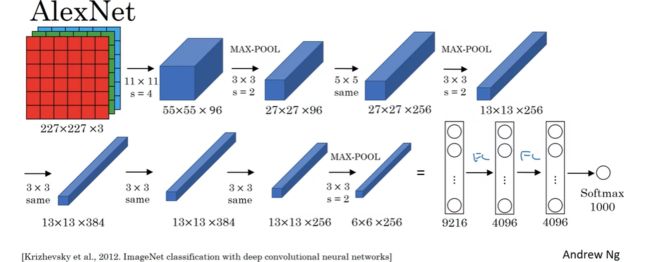
原文中输入图像是 224x224x3 的，但如果检查数字，会发现227x227才合理。相对 于 LeNet-5，AlexNet 采用相似的构造，但 AlexNet 大概有 6 千万参数，拥有更多隐藏神经元，在更多数据上训练（比如ImageNet） AlexNet 使它能有优秀的性能。此外，使 AlexNet 比 LeNet 更好的另一因素是 ReLU 激活函数的使用。

原文中还提出的一些方法：
1、在两块GPU上训练网络。
2、原始的 AlexNet 还有另一种层，叫做局部响应归一层(LRN) ，它是对特征图的一种归一化。但因为并不怎么管用，所以 LRN 实际上用得很少，我们不用花太多时间去理解 LRN。

AlexNet 让大部分计算机视觉领域的研究者开始认真对待深度学习，确信深度学习对计算机视觉有用。随后深度学习对计算机视觉和其他领域产生了巨大影响。

1.1.3 VGG（VGG-16）

VGG 网络中共有 16 个带权重 W 的层，所以也叫 VGG-16 网络。VGG-16结构更简单，更关注卷积层。

论文原文：《Very Deep Convolutional Networks for Large-Scale Image Recognition》

网络结构：
1、卷积过滤器：都是 3x3 大小，步长为 1 ，采用 “same” 填充。
2、池化层过滤器：都是 2x2 大小，步长为 2。
3、特征图成倍增加，而对应的深度成倍减少。

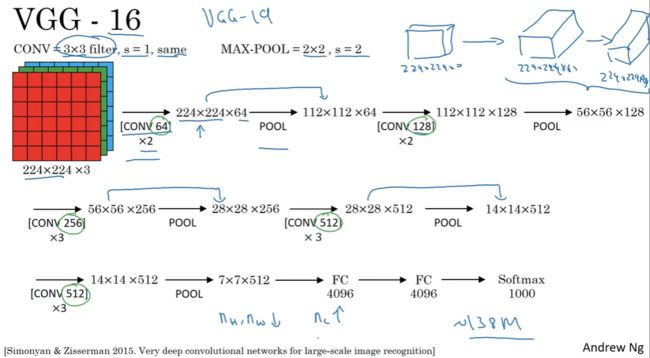
VGG-16 的结构相当简洁性和统一。但也有一个很大的缺点，即：该网络有16层带权重的层，这是个相当大的网络，总共有1亿 3 千 8 百万个参数。即使以现在标准衡量也是很大了。

VGG-19 那是 VGG-16 的更大版本，然而由于VGG-16跟VGG-19的性能差不多，很多人会用VGG-16。

1.2 ResNet（残差网络）

1.2.1 什么是 ResNet

残差块（Residual block）:
这里有两层神经网络。正常情况下，从输入 $a^{[l]}$ 到输出 $a^{[l+2]}$，会经过 linear→relu→linear→relu这些步骤，称之为主路线，也就是图中绿色的路线。

如果把 $a^{[l]}$ 然后把它往前复制到靠后后的位置， 然后在激活函数中与 $z^{[l+1]}$ 一起参与$a^{[l+2]}$ 的计算，这被称作快捷路径（short cut）或者跳跃连接（skip connection）。而跳跃连接的起点与终点之间的层，就组成为了一个残差块（Residual Block）。

残差网络（residual Network）
ResNet的发明者 是Kaiming He，Xiangyu Zhang， Shaoqing Ren，和Jian Sun。 他们发现使用残差块可以训练更深层的神经网络。 通过堆叠大量的残差块，就可以形成一个残差网络（residual Network）

普通网络（Plain）与残差网络（ResNet）的对比：

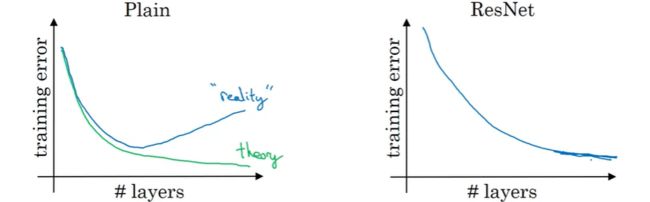
如果你使用普通的神经网络，理论上来讲，一个更深层次的网络只会有帮助，层数越深最终的误差就会越小。 但在实践中，由于梯度消失或梯度爆炸问题，一个很深的普通网络意味着你的优化算法训练起来会更困难，所以，当层数超过一定数量时则训练误差反而会更糟。

但有了ResNet的情况是，即使层数越来越深, 你仍可以让训练误差继续下降，这可以有效的解决梯度消失和爆炸问题，使得我们可以训练更深的神经网络而不会看到性能倒退的现象。

1.2.1 为什么 ResNet 有效

以 X 作为输入，输入到某个大型神经网络，并输出a[l]。
如果在这里你要调整神经网络使其层数更深一点， 我们将要在相同的 Big NN 后再额外增加两层，然后输出a[l+2]， 再把新增的两层做成 ResNet 块。

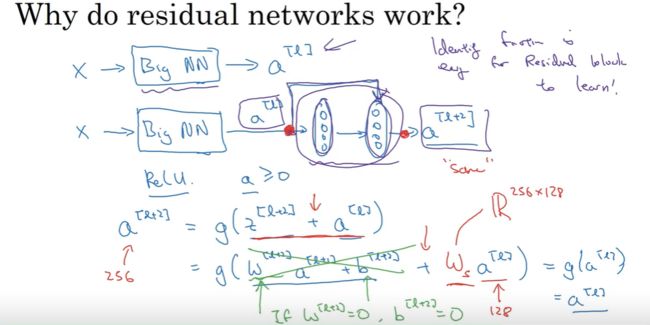
为了证明我们的观点，在这整个神经网络中我们用Relu激活函数，那么所有激活 (a) 都将会大于等于0。实现跳跃连接后，有：$$a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$$将其展开得：$$a^{[l+2]}=g(W^{[l+2]}\ast a^{[l+1]}+b^{[l+2]}+a^{[l]})$$如果你这里用 L2 正则化，那么这将会减小 $W^{[l+2]}$ 和 $b^{[l+2]}$ 的值，且很容易减小至：$$w^{[l+2]}=0$$ $$b^{[l+2]}=0$$那么则有：$$a^{[l+2]}=g(a^{[l]})=relu(a^{[l]})=a^{[l]}$$

由于跳跃连接也很容易得到 $a^{[l+2]}=a^{[l]}$，这意味着残差块比较容易学习恒等函数。 换句话说，将这两层加入到你的神经网络后，与上面这个没有这两层的网络相比并不会使神经网络的性能变差。而当这里所有参数都学习到有意义的数值的话，可能要比学习恒等函数更好。

另一个值得讨论的细节是，要实现 $a^{[l+2]}=g(z^{[l+2]}+a^{[l]})$，则需要$z^{[l+2]}$ 和$a^{[l]}$ 是同维度的。如果它们的维度不同，则需要进行一个转换，即：$a^{[l+2]}=g(z^{[l+2]}+W_s{a}^{[l]})$，其中 $W_s$ 的行数与 $z^{[l+2]}$ 的行数同高， $W_s$ 的列数与 $a^{[l]}$ 的行数相同。此外，$W_s$ 可以是一个包含已学习到的参数的矩阵， 也可以是一个固定的矩阵。

1.3 Inception Network

1.3.1 1x1的卷积操作

1x1的卷积能做些什么呢？难道不就是数的相乘吗？这看起来是一件很滑稽的事，事实并非完全如此。

用一个 1x1x1 的过滤器对一个 6x6x1 的图像做卷积，最终只是把这整张图像乘以某个数字，看起来没什么作用。但对于一个 6x6x32 的图像，和一个 1x1 的过滤器做卷积会很有意义。这时这个 1x1 的过滤器就类似于一个神经元，接收 32 个特征的输入向量。 而若有多个 1x1 的过滤器，则就会组成一个全连接层。所以1x1的卷积也被称作网中网。这种思想有很大的影响力，其影响了许多神经网络架构，包括著名的 Inception network 。

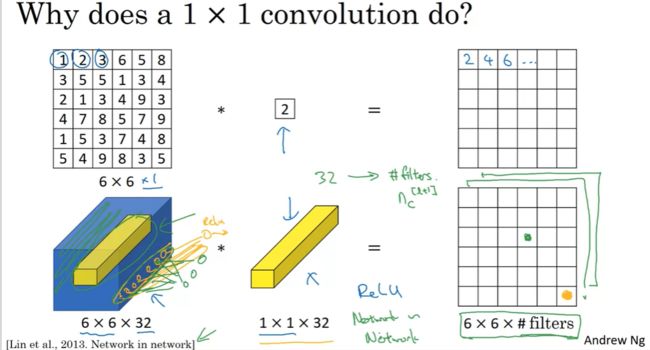
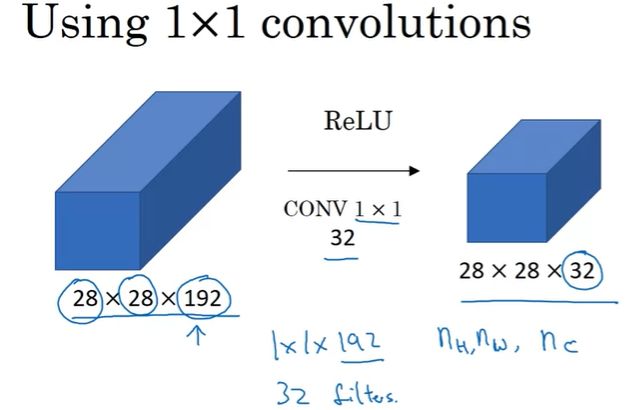
举一个1x1 卷积有应用价值的例子，我们知道池化操作可以通过减小图像大小（n_H和 n_W）的方式来减少计算量，但如果通道数过大，我们就想缩小它，又该怎么办呢？ 1x1的卷积则可以解决这个问题。比如，对于一个 28x28x192 的特征图，可以通过使用 32 个 1x1x192 的过滤器使其缩小到 28x28x32，通道数 n_C 则由原来的192变成了32。

1.3.2 Inception Module

论文原文：《Going deeper with convolutions》

一、单纯的 Inception Module

在为卷积神经网络设计某一层时，可能会面临如下选择：
1、这一层是用来卷积还是池化？
2、这一层需要多少组过滤器？
3、每个过滤器尺寸与通道数的设置？

但往往在设计之前，我们并不知到到底是用卷积还是池化对最终结果最好，也不知道过滤器的个数、尺寸、通道取何值时网络性能最优。所以 Inception Network 的核心思想就是在一个模块中同时进行卷积与池化操作，且多组不同的过滤器并行进行工作并输出大小（n_H和n_W）相同的特征矩阵，然后把所有的输出结果都连接起来，然后让神经网络去学习它过滤器中的参数。

所以，当构建一个 Incetion 网络时，你不需去决定到底是用 1x1、3x3 还是 5x5 的卷积核或者是否使用 pooling，Inception 网络会将它们一起组合到网络中来。

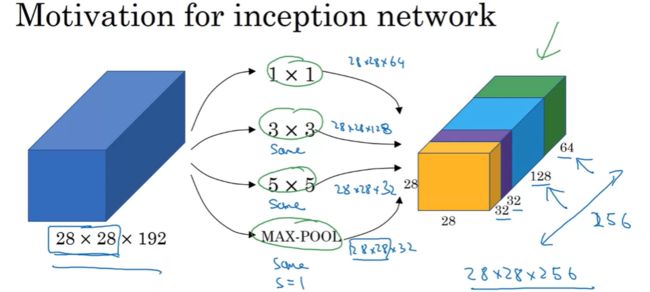
二、用 1x1 的过滤器减少计算量

但这样的话又会导致计算量增大的问题，拿上图中这 32 个 5x5x192 的卷积核来举例，28x28x192 的输入在经过它的卷积操作，输出为 28x28x32。其计算量为：$$(5\ast 5\ast 192)\ast (28\ast 28\ast 32)\approx 120M$$结果等于 1.2 亿，虽然你可以在现代的计算机里做 1.2 亿次乘法运算，但是这个计算成本还是相当大的。

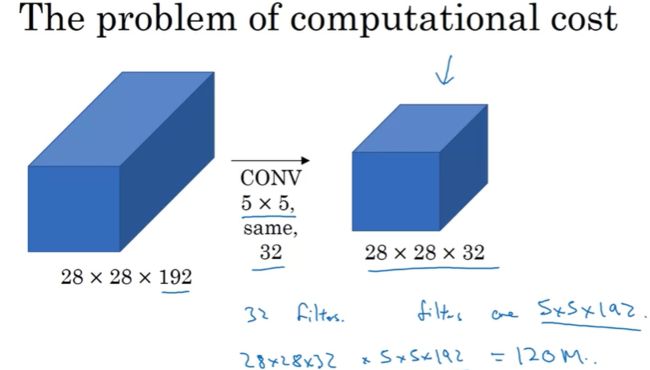
我们可以使用 1x1 过滤器，把计算成本降低到大约 1/10 左右。

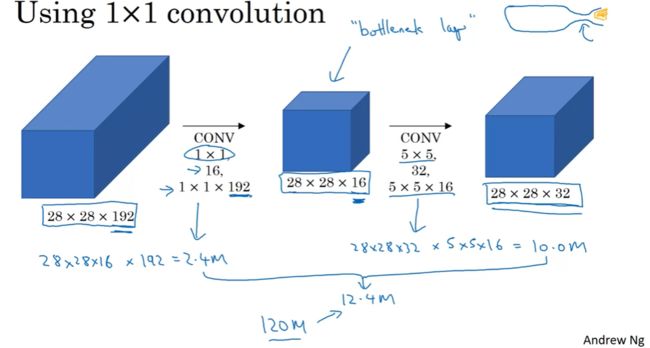
我们先使用 16 个 1x1x192 的过滤器进行卷积操作，接着再使用 32 个 5x5x16 的过滤器进行第二次卷积，输出为 28x28x32。则其计算量为：$$(1\ast 1\ast 192)\ast (28\ast 28\ast 16)+(5\ast 5\ast 16)\ast (28\ast 28\ast 32)\approx 2.4M+10M\approx 12.4M$$ 相同维度的输入和输出，在使用 1x1 的过滤器后，运算成本却从原来的 $120M$ 变为 $12.4M$，只相当于原先的大概 $1/10$。

而这 1x1 的过滤器这一层又称作 “瓶颈层”，大概是因为输入就像是瓶身，在经过 1x1 的卷积操作后数据变少了很多，而又经过 5x5 的卷积操作后，输出的数据又多了一些，就像是瓶口一样。

三、加入 1x1 过滤器之后的 Inception Module

在 Inception Module 中，除了本来就有一个 1x1 的卷积核之外，还在两类地方插入了 1x1 的过滤器：
1、卷积操作之前，
2、池化操作之后。
且都是通过起减少通道数（n_C）的方式来减少数据量，从而降低计算成本。

1.3.3 Inception Network

一个 Inception Module：

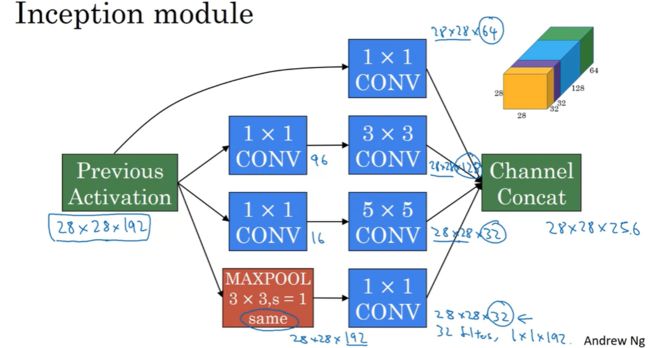
在 Inception Network 中堆叠了多个类似于这样的 Inception Module。它的最后几层是全连接层，用来计算最终的分类结果。此外，还可以在网络中间的某些 Inception Module 后接上一个全连接网络，这些旁支也是用于计算分类结果。

下图则是 Inception Network 结构图，输入在左，输出在右。
其中：
蓝色 —— 卷积层、全连接层
深橙色 —— 池化层
黄色 —— softmax 输出层

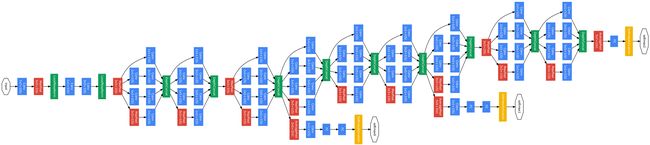
这里这个 Inception网络 是 google 的工程师开发的，又为了纪念 LeNet，所以把它称作 GoogleNet。

2 使用 ConvNet 的实用建议

2.1 使用开源实现

如果你看到一篇论文并想实现它，你需要考虑的是上网寻找一个开源的实现，因为如果你可以得到作者的实现，那么通常这比你从头实现更节省时间，尽管有时候从头实现一次也是很好的锻炼。比如假如你对残差网络很感兴趣且想要实现它，那么我们首先输入 “ResNet github” 并这对关键词进行搜索，你可以看到关于 ResNet 的很多不同的实现。

现在 你已经开始开发一个计算机视觉图像应用 在这个过程中最常见的流程从选取一个你喜欢的框架开始，然后去找一个开源的代码实现去github上下载好。然后可以在下载好的代码上开发。这些网络可能需要很长的时间来训练，也许有人已经用多个GPU 和大数据集训练好了，这样你就可以直接对这些网络使用迁移学习。

2.2 迁移学习

计算机视觉的研究社区很擅长把许多数据库发布在网络上，如ImageNet MSCOCO PASCAL等数据库等，许多计算机视觉的研究者已经在上面训练了自己的算法，有时算法训练要耗费好几周时间、使用很多GPU。这是一个痛苦的调试过程。

如果我们想实现一个计算机视觉应用，通常更快捷的方式是：下载已经训练好权重和网络结构，把这个作为预训练 迁移到你感兴趣的新任务上，然后再进行微调。

迁移学习有个规律：自己手头的数据越多，迁移学习时可以微调的参数量就可以相应的增加。

两种做法：
1、利用迁移学习策略，训练时冻结部分网络参数，只修改后面一层或几层的参数。
2、把不需要学习的层取出来，将所有样本通过这些层，得到对应的特征向量。将后几层看成一个神经网络，并用刚刚得到的特征向量训练这个神经网络。

2.3 数据扩充

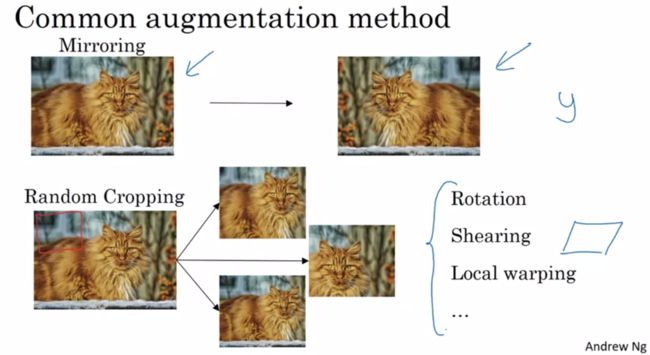
在计算机视觉领域中，绝大多数算法会面临不能获得足够数据的问题。这意味着当训练计算机视觉模型时，数据扩充常常会有所帮助。无论你是用迁移学习还是从零开始训练你自己的模型，这点都是成立的。下面是一些常见的数据扩充方法。

第一类：镜像、裁剪、旋转、局部变形

第二类：色彩变换