数据结构与算法分析(Java语言描述)—— 树
1.二叉树
1.1 简述
二叉树(binary tree)是一棵树,其中每个节点都不能有多于两个的儿子
左图显示一棵由一个根和两棵子树组成的二叉树,子树 Ta 和 Tb 均可能为空。
二叉树的一个性质是一棵平均二叉树的深度要比节点个数 N 小得多,这个性质有时候很重要。分析表明,其平均深度为 O(根号N),而对于特殊的二叉树,即二叉查找树,其深度的平均值为O(log N).不幸的是这个深度可以大到 N–1。
1.2 实现
class BinaryNode{
Object element;
BinaryNode left;
BinaryNode right;
}1.3 例子:表达式树
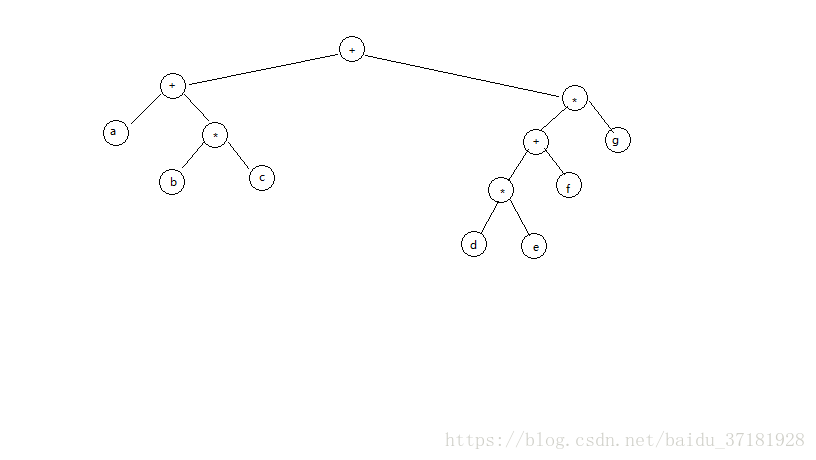
上图显示一个表达式树的例子。表达式树的树叶是操作数,如常数或变量名,而其他的节点为操作符。由于这里所有的操作都是二元的,因此这棵特定的树正好是二叉树,虽然这是最简单的情况,但是节点还是有可能含有多于两个的儿子。一个节点也有可能只有一个儿子,如具有一目运算符的情形。我们可以将通过递归计算左子树和右子树所得到的值应用在根处的运算符上而算出表达树T的值。在本例中,左子树的值是 a + (b * c),右子树的值是((d * e) + f) * g,故此整个树表示 (a + ( b * c)) + (((d * e) + f) * g)
一般的方法(左,节点,右)称为中序遍历,由于其产生的表达式类型,这种遍历很容易记忆。
另一种遍历策略是递归地打印出左子树、右子树,然后打印运算符。如果我们将这种策略应用于上面的树,则将输出 a b c * + d e * f + g * c +,显而易见,他就是后缀表达式法。这种遍历策略一般称为后序遍历。
第三种遍历策略是先打印出运算符,然后递归地打印出右子树和左子树。此时得到的表达式 + + a * b c * + * d e f g 是不太常用的前缀记法,这种遍历策略称之为先序遍历。
构造表达式树
看一个例子。设输入为:a b + c d e + * *
前两个符号是操作数,因此创建两棵单节点树并将它们压入栈中
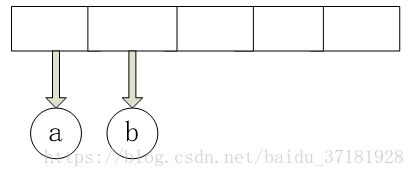
接着 “+” 被读入,因此两棵树被弹出,一颗新的树形成,并被压入栈中。
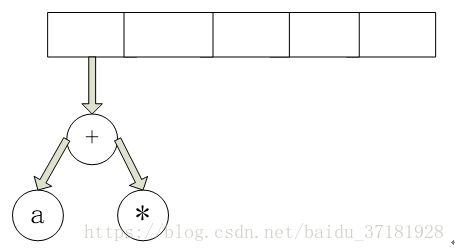
然后 c,d 和 e 被读入,在每个单节点树创建后,对应的树被压入栈中。
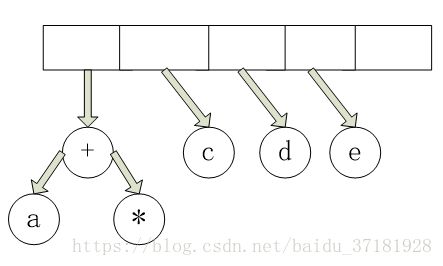
接下来读入 “+” 号,因此两棵树合并。
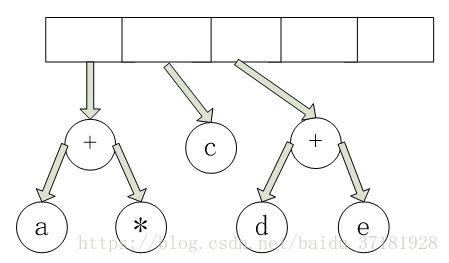
继续进行,读入 * 号,因此,我们弹出两棵树并形成一棵新的树,* 号是它的根。
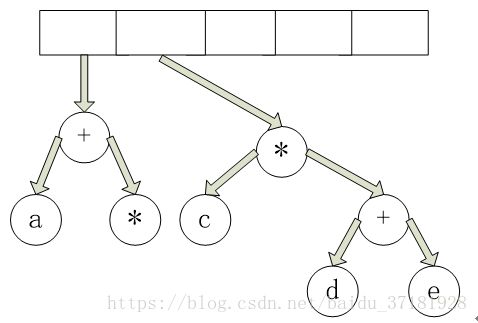
最后,读入最后一个符号,两棵树合并,而最后的树被留在栈中。
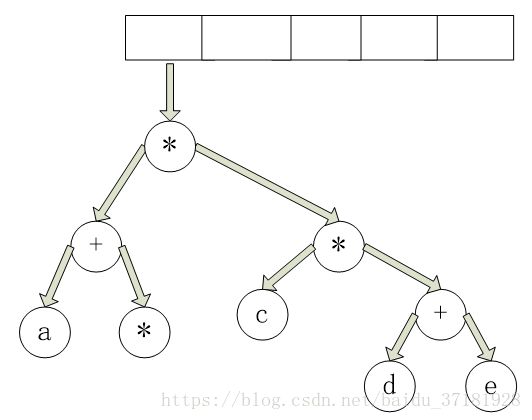
package com.anqi.binaryNode;
public class BinaryNode {
String element;
BinaryNode left;
BinaryNode right;
public BinaryNode(String element) {
this.element = element;
}
public BinaryNode(String element, BinaryNode left, BinaryNode right) {
this.element = element;
this.left = left;
this.right = right;
}
public void setElement(String element) {
this.element = element;
}
public String getElement() {
return element;
}
public void setLeft(BinaryNode left) {
this.left = left;
}
public BinaryNode getLeft() {
return left;
}
public void setRight(BinaryNode right) {
this.right = right;
}
public BinaryNode getRight() {
return right;
}
}package com.anqi.binaryNode;
import java.util.Scanner;
public class ExpressionTree {
/**
* 构造表达式树的静态方法。
* 遍历表达式,若为操作数则构造单节点树压入stack,若为操作符,则弹出两个节点,与
* 操作符构造成新的树,再压入stack中。最后stack中只剩一个节点,该节点就是我们要求的
* 表达式树。
* @param expressions 后缀表达式分解过后的字符串数组
* @return 表达式树
*/
public static BinaryNode postfixToExpressionTree(String[] expressions){
BinaryNode operand1; //用于暂存弹出的BinaryNode节点
BinaryNode operand2;
Stack stack = new Stack(); //用于构造表达式树的栈
for (String s:expressions) { //遍历表达式
if (s.equals("+") || s.equals("-") || s.equals("*") || s.equals("/")){
operand1=stack.pop(); //弹出操作数
operand2=stack.pop();
stack.push(new BinaryNode(s,operand2,operand1)); //构造成新树并压入栈中
}else {
stack.push(new BinaryNode(s));
}
}
return stack.pop();
}
/**
* 打印二叉树的方法。
* 通过递归调用来打印二叉树。并在节点前缩进了与深度相当的空格,方便观察。
* @param depth 当前节点在树中的的深度
* @param binaryNode 当前树节点
*/
public static void printBinaryTree(int depth,BinaryNode binaryNode){
for (int i=0;i//打印与深度相当的缩进
System.out.print(" ");
}
System.out.println(binaryNode.getElement()); //打印当前节点的数据
if (binaryNode.getLeft() != null){ //若左子树不为空,那么递归调用打印方法,打印左子树
printBinaryTree(depth+1,binaryNode.getLeft());
}
if (binaryNode.getRight() != null){ //若右子树不为空,那么递归调用打印方法,打印右子树
printBinaryTree(depth+1,binaryNode.getRight());
}
}
/**
* 测试构造和打印表达式树的方法。
* main()方法用于测试,负责接收表达式并将其拆解成字符串数组,传递给
* postfixToExpressionTree方法,然后调用printBinaryTree方法打印返回的表达式树。
* @param args 忽略
*/
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine(); //接收表达式
String[] splits= s.split(""); //分解成字符串数组
BinaryNode binaryNode=postfixToExpressionTree(splits); //构造比表达式树
printBinaryTree(0,binaryNode); //打印表达式树
}
}
/*输出结果
*
+
a
b
*
c
+
d
e
*/
2.查找树 ADT —— 二叉查找树
使二叉树成为二叉查找树的性质是,对于树中的每个节点X,它的左子树中所有项的值小于X项中的项,而它的右子树中所有项的值大于X中的项。
由于树的递归定义,通常是递归地编写这些操作的函数。因为二叉查找树的平均深度是O(logN),所以不用担心栈空间被用尽。
public class BinarySearchTree <AnyType extends Comparablesuper AnyType>> {
private static class BinaryNode<AnyType>{
AnyType element;
BinaryNode left;
BinaryNode right;
public BinaryNode(AnyType element, BinaryNode left, BinaryNode right) {
this.element = element;
this.left = left;
this.right = right;
}
public BinaryNode(AnyType element) {
this(element, null, null);
}
}
//树的根节点
private BinaryNode root;
public BinarySearchTree() {root = null;}
public void makeEmpty() {root = null;}
public boolean isEmpty() {return root == null;}
public boolean contains(AnyType x) {return contains(x, root);}
public AnyType findMin() {
if(isEmpty())
throw new BufferUnderflowException();
return findMin(root).element;
}
public AnyType findMax() {
if(isEmpty())
throw new BufferUnderflowException();
return findMax(root).element;
}
public void insert(AnyType x) {
root = insert(x, root);
}
public void remove(AnyType x) {
root = remove(x, root);
}
public void printTree() {}
/**
* 注意调试的顺序。关键的问题是首先要对是否空树进行测试,否则我们就会生成一个企图通过 null 引用
* 访问数据域的 NullPointerException 异常。剩下的测试应该使得最不可能的情况安排在最后进行。还要
* 注意的是,这里的两个递归都是尾递归并且可以用一个 while循环很容易地代替。尾递归的使用在这里是合
* 理的,因为算法表达式的简明性是以速度的降低为代价的。而这里使用的栈空间不过是 (logN)。
*/
private boolean contains(AnyType x, BinaryNode t) {
if(t == null)
return false;
int compareResult = x.compareTo(t.element);
if(compareResult < 0)
return contains(x, t.left);
else if(compareResult > 0)
return contains(x, t.right);
return true;
}
/**
* findMin 的递归实现
*/
private BinaryNode findMin(BinaryNode t) {
if(t == null)
return null;
else if(t.left == null)
return t;
return findMin(t.left);
}
/**
* findMax 的非递归实现
*/
private BinaryNode findMax(BinaryNode t) {
if(t != null)
while(t.right != null)
t = t.right;
return t;
}
private BinaryNode insert(AnyType x, BinaryNode t) {
return null;
}
private BinaryNode remove(AnyType x, BinaryNode t) {
return null;
}
private void printTree(BinaryNode t) {}
} 3. AVL 树
4. 伸展树
5. 再谈树的遍历
public void printTree(){
if(!isEmpty())
System.out.println("Empty Tree");
else
printTree(root);
}
public void printTree(BinaryNode t){
if(t != null){
printTree(t.left);
System.out.println(t.element);
printTree(t.right);
}
} 中序遍历(由于它依序列出了各项,因此是有意义的)
这个算法的有趣部分除它简单的特性之外,还在于其总的运行时间是O(N)。这是因为在没有一个节点进行的工作是常数时间,每一个节点访问一次。
有时候我们需要先处理两颗子树然后才能处理当前节点。例如,为了计算一个节点的高度,首先需要知道它的子树的高度。叫做后序遍历
我们将叶子结点高度规定为0;
private int height(BinaryNode t){
if(t == null)
return -1;
else
return 1 + Math.max(height(t.left) + height(t.right));
} 第三种遍历是先序遍历。这里,当前节点在其儿子节点之前处理,这种遍历是有用的。比如要想用深度标记每一个节点,那么这种遍历就会被用到。
所有遍历方法都有一个共同的观点,就是先处理 null 的情形,然后才是其他的工作。注意:此处少一些附加的变量,这样程序更紧凑,犯错误可能性越低。