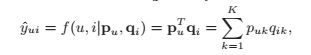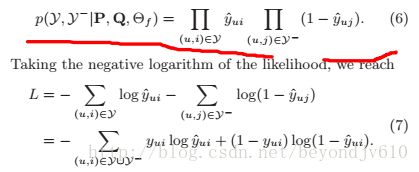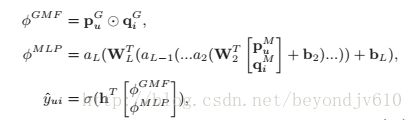Neural Collaborative Filtering（NCF）(a improvement to MF)

这篇文章主要是用深度学习做推荐，发表在WWW上的，NUS的何向南博士

代码地址：https://github.com/hexiangnan/neural_collaborative_filtering

下面是本人对文章的一些总结

一、矩阵分解（matrix factorization）

在这里K代表潜空间的维度。user和item的潜空间维度必须保持一致(如果不一致无法计算内积)。其实质上是相当于用K维的潜特征来代表每一个user和item，并通过计算每个user和item的潜特征的内积来得到最后的预测结果。由于其假定各个潜特征之间相互独立，其本质上是特征的线性组合的结果。比如对于同一个用户，那么其用户的潜特征是相同的，其对不同项目的评分的差别来源于不同项目的潜特征不同。对于同一个项目，其项目的潜特征是一致的，不同用户对其的评分差别来源于用户的潜特征不同。

但是这种线性组合的结果会带来以下的问题。

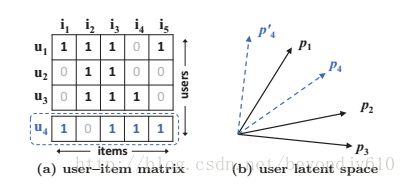
上图中的（a）代表user-item的得分矩阵，如果我们采用Jaccard系数作为相似度的衡量指标（当然也可以用其他的）。Jaccard系数的值等于两个用户项目的交集中项目个数除以其并集中的项目个数，计算可得S23(0.66)> S12(0.5)> S13(0.4) ，所以用户1,2,3的相关关系可以由图b表示。而对于用户4，其与前三个用户的相关系数分别为s41(0.6)> s43(0.4)> s42(0.2) ，即用户4与用户1关系最大，与用户3关系次之，与用户2关系最小。此时，无论将用户4画在用户1的左上方还是右下方，此与用户2的距离都会小于与用户3的距离，这与用户4为用户3的相似度大于与相互2的相似度这一结论。可见，在二维空间里面（潜变量的维数为2），无法真正表示用户之间的关系。解决方法之一就是增加潜特征的维数，但是随着用户数或者项目数的增加，潜特征也需要跟着增加，大量的增加潜特征会导致模型的过拟合，特别是对于稀疏的数据。作者提出Neural Collaborative Filtering（NCF）正是为了解决这一问题。

二、NEURAL COLLABORATIVE FILTERING

2.1通用框架：

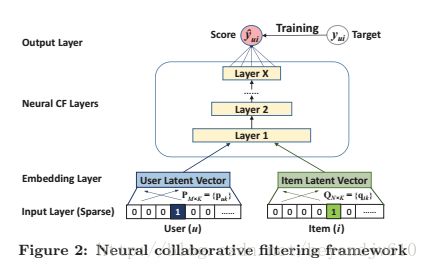
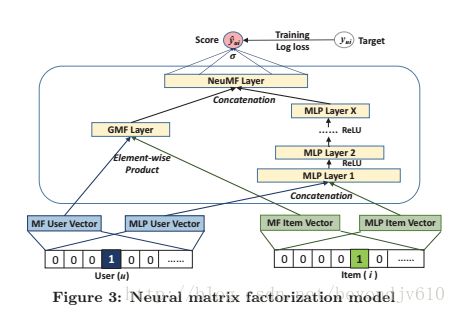
其输入层是包括两个部分，第一部分是用户的one-hot编码，第二部分是项目的one-hot编码。对于这两部分的输入，分别通过两个全连接的网络得到用户的潜变量和项目的潜变量，这两个结果作为embedding layer。用户的潜变量和项目的潜变量合并作为NCF的输入，这里的合并是指可以是两两元素对应相乘（因而要求用户的潜变量维度和项目的潜变量维度是一致的，这个跟矩阵分解一样），也可以是将两个向量串联成一个向量。对于NCF layers，其一共包括X层，每一层的神经元个数是递减的（塔型的网络结构），这样有利于更好地去提取抽象的特征，每一层的激活函数都用Relu，最后一层的输出结果就是预测值。故可以将NCF表示为：

这里P,Q分别是用户和项目的潜变量矩阵（将onehot转化为embedding layer），theta是NFC layer的神经网络参数，这三个变量都是通过学习得到的。

2.1.1NFC网络的训练

由于NFC网络的输出层就是预测结果，显然我们可以用MSE作为损失函数并使用SGD或者ADAM等算法求得网络的参数。

上图中w代表权重矩阵，yUy-中y代表值为1的结果（即用户与项目发生了互动，可能是观看，点击，收藏等），正样本，y-表示用户与项目之间没有互动，负样本。由于正样本数会远远大于负样本数，为了避免样本不平衡问题，可以对负样本进行抽样以保证样本数量平衡。考虑到数据集的值为0,1，我们可以将其理解成一个二分类的问题，从概率的视角求其似然值来作为目标函数。

通过求对数并做简单的变换可以将其转化成二分类的交叉熵的损失函数。

2.2 一般化矩阵分解Generalized Matrix Factorization (GMF)

NCF是MF的一般化的结果。对于输入层到embedding层，，无论是NCF还是MF都是讲onehot的编码转化为潜特征。从embedding到NCF层，如果NCF采用将两个潜变量对应的元素相乘（神经网络在处理两个向量时通常将其串联起来，但对应元素相乘也是可行的），并且将后面所有层的参数都设置为单位矩阵，那么NCF与MF就是相同的，因而可以将MF看做是NCF的一个特例。

2.3多层感知机Multi-Layer Perceptron (MLP)

在GMF中，我们得到潜变量之后，将其对应的元素两两相乘来作为NCF的输入，另外一种可行的作为则是将两个潜变量串联成一个变量作为NCF层的输入，然后在通过MLP来得到最后的预测值。

2.4 GMF与MLP两者的融合（NeuMF）

一种简单的融合方法（NTN）根据embedding层的输出层（用户的潜特征和项目的潜特征），同时采用对应元素相乘和串联的方法得到两个变量，再将这两个变量串联起来作为MCF层的输入，其可表示为：

上述方法的缺点在于由于需要进行向量的对应元素相乘，因而需要保证用户的前特征和项目的潜特征的数量是一致的。然后在现实中，用户数和项目数的差别可能很大，为了得到相同数量的潜特征会使得潜特征失去一定的表达能力。本文的作者采用的是对用户和项目分别建立两个潜特征，对于第一个潜特征，要求用户潜特征的维数和项目潜特征的维数是相等的，保证可以用于GMF，而第二个潜特征不要求用户潜特征更和项目潜特征的维数是一致的，给与潜特征更大的表达能力。其框架图如下：

数学表示为：

2.4.1混合模型的预训练

由于NeuMF是非凸的，只能求得局部最优而无法得到全局最优，因而初始化的好坏对模型的结果会产生较大的影响。由于NeuMF是GMF和MLP模型的融合，因而我们采用训练好的GMF和MLP参数作为NeuMF模型的初始化参数。但是我们在NeuMF模型的输出层，我们在GMF和MLP模型的系数前面分别加上a和（1-a），这里的a是超参数。如下图所示：

这里的hGMF和hMLP就是GMF和MLP输出层的系数，这种做法可以理解为将MLP和GMF进行加权平均，这里的a是权重。