DP入门题总结

DP入门题总结

2020年4月7日更新
主要更新了：LCS的滚动数组求法，以及LIS的O(nlogn)做法

ps：一些DP简单入门题汇总，仅供自己复习所用，如有错误，还望指出（而且这全是入门级别题）

动态规划（dynamic programming），简称DP，这一类题目可以说是算法竞赛中最为灵活的内容之一，需要经验，有时候也需要一点灵感，如果能找到要转换的状态，题目看上去就会很简单。
动态规划程序设计是对解最优化问题的一种途径、一种方法，而不是一种特殊算法。
这类题目可以出的很难，区间DP，树形DP，数位DP，概率DP等等，这里只介绍了最简单的线性DP和二维DP。

DP中最重要的就是寻找状态转移方程

---

A-楼梯问题

---

Problem Description
有一楼梯共M级，刚开始时你在第一级，若每次只能跨上一级或二级，要走上第M级，共有多少种走法？
Input
输入数据首先包含一个整数N，表示测试实例的个数，然后是N行数据，每行包含一个整数M（1<=M<=40）,表示楼梯的级数。
Output
对于每个测试实例，请输出不同走法的数量
Sample Input
2
2
3
Sample Output
1
2

题解：这道题就是一道简单的DP题，
当求上第n级楼梯时共有多少种走法时就是第n级的状态，
而状态转移方程我们很容易知道：
f[n]=f[n-1]+f[n-2]

这题代码实现也有三种实现方法：填表法、刷表法、记忆化搜索
这里就直接采用填表法，直接预先打表（身为小白的我最喜欢的就是打表）

#include
#define ll long long
using namespace std;
ll f[100];
int main()
{
    for(int i=1;i<=40;i++)
    {
        if(i==1||i==2)
            f[i]=1;
        else
            f[i]=f[i-1]+f[i-2];     //状态转移方程
    }
    ll n;
    ll m;
    scanf("%lld",&n);
    while(n--)
    {
        scanf("%lld",&m);
        printf("%lld\n",f[m]);
    }
    return 0;
}

B-数塔问题

下图是个数字三角，请编写一个程序计算从顶部至底部某处一条路径，使得该路径所经过的数字总和最大。

7

3 8

8 1 0

2 7 4 4

1． 每一步可沿左斜线向下或右斜线向下走；

2． 1<=三角形行数<=100

3． 三角形中的数字为整数 0，1，……，99。

4． 如果有多种情况结果都最大，任意输出一种即可。

输入：

第一行一个整数N，代表三角形的行数。

接下来N行，描述了一个数字三角。

输出：

第一行一个整数，代表路径所经过底数字总和。

第二行N个数，代表所经过的数字。

样例输入：
4
7
3 8
8 1 0
2 7 4 4

样例输出：
25
7 3 8 7

题解：当然这道题也是一道DP水题，
于是以：f[i][j]表示从第i行第j列个元素所在位置到三角形底部所经过的数字总和的最大值

状态转移方程为：f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j]

当然这道题有两种方法，一种从顶部向底部推，一种从底部向顶部推，这里采用从底部向顶部推，
于是代码如下：

#include
using namespace std;
int main()
{
    int a[105][105],f[105][105];
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<=i;j++)
            scanf("%d",&a[i][j]);
    }
    for(int i=0;i<n;i++)
        f[n-1][i]=a[n-1][i];             //先将最后一行存入到f数组中
    for(int i=n-1;i>=0;i--)
    {
        for(int j=0;j<=i;j++)
            f[i][j]=max(f[i+1][j],f[i+1][j+1])+a[i][j];     //状态转移方程
    }
    printf("%d\n",f[0][0]);
    int num,j=0;
    printf("%d",a[0][0]);
    for(int i=1;i<n;i++)      //寻找所经过的数
    {
        num=f[i-1][j]-a[i-1][j];
        if(num==f[i][j+1])
            j++;
        printf(" %d",a[i][j]);
    }
    printf("\n");
    return 0;
}

C:0-1背包问题

ps：当然这里的0-1背包问题是最为基础的，裸的0-1背包

B - Bone Collector HDU -2602

Many years ago , in Teddy’s hometown there was a man who was called “Bone Collector”. This man like to collect varies of bones , such as dog’s , cow’s , also he went to the grave …
The bone collector had a big bag with a volume of V ,and along his trip of collecting there are a lot of bones , obviously , different bone has different value and different volume, now given the each bone’s value along his trip , can you calculate out the maximum of the total value the bone collector can get ?

Input

The first line contain a integer T , the number of cases.
Followed by T cases , each case three lines , the first line contain two integer N , V, (N <= 1000 , V <= 1000 )representing the number of bones and the volume of his bag. And the second line contain N integers representing the value of each bone. The third line contain N integers representing the volume of each bone.

Output
One integer per line representing the maximum of the total value (this number will be less than 2 31).

Sample Input

1
5 10
1 2 3 4 5
5 4 3 2 1

Sample Output
14

题解：可以看出这就是一道裸的0-1背包问题，于是分析其状态以及状态转移方程
状态：
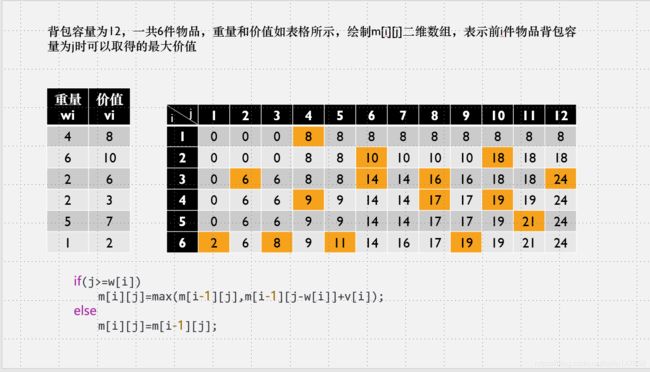
前i个物品，背包容量为j时，可以获得最大价值

状态转移方程：
面对第 i 个物品时，无非就是拿或者不拿两种选择
如果此时背包的容量 j < 该物品的重量 w[i]
装不下只能选择不拿：m[ i ][ j ] = m[ i-1 ][j]
若 j >= w[i]，
选择拿，则需要腾出w[i]的空间，获得价值为 m[ i-1 ][ j-w[i] ] + v[i]
选择不拿，则和上面情况一样，m[i-1][j]
两者取最大值
即：
if(j>=w[i])
m[i][j]=max(m[i-1][j],m[i-1][j-w[i]]+v[i]);
else
m[i][j]=m[i-1][j];

例如：
于是这道题代码如下：

朴素做法：

#include
#include
#include
#include
using namespace std;
int value[1010],weight[1010],m[1010][1010];          
//分别表示骨头的价值，重量，以及状态转移方程    重点解释m[i][j]：i表示价值域，j表示重量域
int t,n,v;
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        memset(value,0,sizeof(value));
        memset(weight,0,sizeof(weight));
        memset(m,0,sizeof(m));
        scanf("%d%d",&n,&v);
        for(int i=1;i<=n;i++)
            scanf("%d",&value[i]);
        for(int i=1;i<=n;i++)
            scanf("%d",&weight[i]);
        for(int i=1;i<=n;i++)
        {
            for(int j=0;j<=v;j++)           //从0开始，意味着重量为0也可以计算
            {
                if(j>=weight[i])
                    m[i][j]=max(m[i-1][j],m[i-1][j-weight[i]]+value[i]);          //状态转移方程
                else
                    m[i][j]=m[i-1][j];
            }
        }
        printf("%d\n",m[n][v]);
    }
    return 0;
}

滚动数组做法：

dp[2][m]版本：

#include
#define lowbit(x) x&(-x)
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const ll mod=1e9+7;
const int maxn=1e5+5;
int n,m;
int v[1010],w[1010];
int dp[2][1010];
int  main() {
    int t;
    scanf("%d",&t);
    while(t--) {
        scanf("%d%d",&n,&m);
        for(int i=1; i<=n; i++) {
            scanf("%d",&v[i]);
        }
        for(int i=1; i<=n; i++) {
            scanf("%d",&w[i]);
        }
        memset(dp,0,sizeof(dp));
        for(int i=1; i<=n; i++) {
            for(int j=0; j<=m; j++) {
                if(j>=w[i])
                    dp[i%2][j]=max(dp[(i-1)%2][j],dp[(i-1)%2][j-w[i]]+v[i]);
                else
                    dp[i%2][j]=dp[(i-1)%2][j];
            }
        }
        printf("%d\n",dp[n%2][m]);
    }
    return 0;
}

dp[m]版本：

#include
#define lowbit(x) x&(-x)
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const ll mod=1e9+7;
const int maxn=1e5+5;
int n,m;
int v[1010],w[1010];
int dp[1010];
int  main() {
    int t;
    scanf("%d",&t);
    while(t--) {
        scanf("%d%d",&n,&m);
        for(int i=1; i<=n; i++) {
            scanf("%d",&v[i]);
        }
        for(int i=1; i<=n; i++) {
            scanf("%d",&w[i]);
        }
        memset(dp,0,sizeof(dp));
        for(int i=1; i<=n; i++) {
            for(int j=m;j>=w[i];j--){
                dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
            }
        }
        printf("%d\n",dp[m]);
    }
    return 0;
}

构造最优解：

#include
#define lowbit(x) x&(-x)
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const ll mod=1e9+7;
const int maxn=1e5+5;
int n,m;
int v[110],w[110];
int dp[110][110];
int vis[110];        //表示物品的状态，0：不装，1：装
int  main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&v[i]);
    }
    for(int i=1;i<=n;i++){
        scanf("%d",&w[i]);
    }
    memset(dp,0,sizeof(dp));
    for(int i=1;i<=n;i++){
        for(int j=w[i];j<=m;j++){
            dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);
        }
    }
    printf("%d\n",dp[n][m]);
    for(int i=n;i>=1;i--){
        if(dp[i-1][m]==dp[i][m]){
            vis[i]=0;
        }
        else{
            vis[i]=1;
            m-=w[i];
        }
    }
    for(int i=1;i<=n;i++){
        printf("%d",vis[i]);
    }
    return 0;
}

D-最长上升子序列

例题：POJ：2533
Sample Input
7
1 7 3 5 9 4 8

Sample Output
4

题解：同样分析其状态以及其状态转移方程
状态：
以f[i]表示前i个数字中以前i个数字结尾所能产生的最长上升子序列
状态转移方程：
f[i]=max(f[i],f[j]+1)

于是代码如下：

朴素做法（O（n^2））

#include
#include
#include
#include
#include
using namespace std;
int a[1010],f[1010];
int main()
{
    int n;
    int num=0;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&a[i]);
        f[i]=1;                //初始化
    }
    for(int i=1; i<=n; i++)
    {
        for(int j=1; j<=i; j++)
            if(a[j]<a[i])
                f[i]=max(f[i],f[j]+1);             //状态转移方程
    }
    for(int i=1;i<=n;i++)
        num=max(num,f[i]);                //找最长上升子序列长度
    printf("%d\n",num);
    return 0;
}

O(nlogn)做法

具体思想：
假设要寻找最长上升子序列的序列是a[n]，然后寻找到的递增子序列放入到数组b中。

（1）当遍历到数组a的第一个元素的时候，就将这个元素放入到b数组中，以后遍历到的元素都和已经放入到b数组中的元素进行比较；

（2）如果比b数组中的每个元素都大，则将该元素插入到b数组的最后一个元素，并且b数组的长度要加1；

（3）如果比b数组中最后一个元素小，就要运用二分法进行查找，查找出第一个比该元素大的最小的元素，然后将其替换。

在这个过程中，只重复执行这两步就可以了，最后b数组的长度就是最长的上升子序列长度。例如：如该数列为：

5 9 4 1 3 7 6 7

那么：

5 //加入
5 9 //加入
4 9 //用4代替了5
1 9 //用1代替4
1 3 //用3代替9
1 3 7 //加入
1 3 6 //用6代替7
1 3 6 7 //加入

最后b中元素的个数就是最长递增子序列的大小，即4。

#include
#include
#include
#include
using namespace std;
int a[1010],b[1010];
int n,len;
int binsearch(int num){
    int l=1,r=len;
    while(l<=r){
        int mid=(l+r)/2;
        if(num>=b[mid]){
            l=mid+1;
        }
        else{
            r=mid-1;
        }
    }
    return l;
}
int main(){
    while(~scanf("%d",&n)){
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        len=1;
        b[1]=a[1];
        for(int i=1;i<=n;i++){
            if(a[i]>b[len]){
                b[++len]=a[i];
            }
            else{
                int pos=binsearch(a[i]);
                b[pos]=a[i];
            }
        }
        printf("%d\n",len);
    }
    return 0;
}

最长上升子序列的构造

#include
#define lowbit(x) x&(-x)
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const ll mod=1e9+7;
const int maxn=1e5+5;
int a[110],dp[110];
int pre[110],path[110];       //pre[]：存上一元素的位置；path[]：存完整最长上升子序列
int main(){
    int n,ans=0;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        dp[i]=1;
    }
    dp[1]=1;
    int r=1;
    for(int i=2;i<=n;i++){
        for(int j=i-1;j>=1;j--){
            if(a[i]>a[j]){
                if((dp[j]+1)>dp[i]){
                    dp[i]=dp[j]+1;
                    pre[i]=j;
                }
            }
        }
        if(dp[i]>ans){
            ans=dp[i];
            r=i;
        }
    }
    int t=0;
    //构造
    while(ans--){
        path[t++]=a[r];
        r=pre[r];
    }
    printf("%d",path[t-1]);
    for(int i=t-2;i>=0;i--){
        printf(" %d",path[i]);
    }
    printf("\n");
    return 0;
}

E-最长公共子序列

例题： POJ：1458
Sample Input
abcfbc abfcab
programming contest
abcd mnp

Sample Output
4
2
0

题解：同样分析其状态与状态转移方程
状态：
以f[i][j]表示第一个字符串S1前i个字符与第二个字符串S2前j个字符所能得到的最长公共子序列
状态转移方程：
if(S1[i]==S2[j])
f[i][j]=f[i-1][j-1]+1;
else
f[i][j]=max(f[i-1][j],f[i][j-1]);
举个例子：

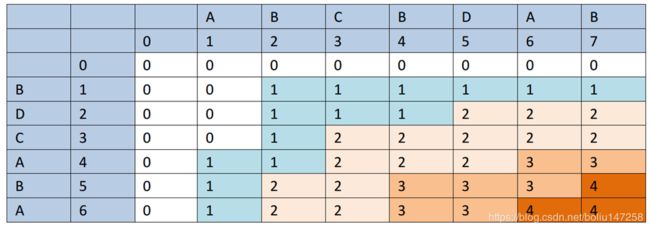
于是上面那题代码如下（字符串采用从1开始编号）：

朴素做法（即空间复杂度：O(n*m）)

#include
#include
#include
#include
using namespace std;
char s1[1010],s2[1010];
int dp[1010][1010];
int main(){
    while(~scanf("%s%s",s1+1,s2+1)){
        int len1=strlen(s1+1);
        int len2=strlen(s2+1);
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(s1[i]==s2[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        printf("%d\n",dp[len1][len2]);
    }
    return 0;
}

滚动数组做法（空间复杂度O(min(n,m)）

稍微解释下滚动数组：
通过状态转移方程可以发现，我们实际上只用到了：当前行和上一行的值，于是我们可以只存这两行的值，然后动态变化。当出现第三行时：用第二行代替第三行，第一行代替第二行。于是我们可以对2取余，从而实现通过奇偶来滚动。

#include
#include
#include
#include
using namespace std;
char s1[1010],s2[1010];
int dp[2][1010];
int main(){
    while(~scanf("%s%s",s1+1,s2+1)){
        int len1=strlen(s1+1);
        int len2=strlen(s2+1);
        memset(dp,0,sizeof(dp));
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(s1[i]==s2[j]){
                    dp[i%2][j]=dp[(i-1)%2][j-1]+1;
                }
                else{
                    dp[i%2][j]=max(dp[(i-1)%2][j],dp[i%2][j-1]);
                }
            }
        }
        printf("%d\n",dp[len1%2][len2]);
    }
    return 0;
}

最长公共子序列的构造：

#include
#define lowbit(x) x&(-x)
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
const ll mod=1e9+7;
const int maxn=1e5+5;
char s1[110],s2[110];
int dp[110][110];
void print(int i,int j){
    if(i==0||j==0)
        return ;
    if(s1[i]==s2[j]){
        print(i-1,j-1);
        printf("%c",s1[i]);
    }
    else if(dp[i-1][j]>dp[i][j-1]){
        print(i-1,j);
    }
    else{
        print(i,j-1);
    }
}
int main(){
    while(~scanf("%s",s1+1)){
        scanf("%s",s2+1);
        int len1=strlen(s1+1);
        int len2=strlen(s2+1);
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(s1[i]==s2[j]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }
        print(len1,len2);
        printf("\n");
    }
    return 0;
}

以上就是一些简单的DP入门题汇总啦！！！

PS:小白发现好像DP中循环以1开始好像方便很多