R语言 Kmeans聚类、PAM聚类、层次聚类、EM聚类

关注微信公共号：小程在线

关注CSDN博客：程志伟的博客

R版本：3.6.1

Kmeans函数：kmeans聚类

pam函数：PAM聚类

hclust函数：层次聚类

cutree函数：层次聚类解

Mclust函数：EM聚类

mclustBIC函数：EM聚类

> ##############对模拟数据的K-Means聚类
> setwd('G:\\R语言\\大三下半年\\数据挖掘：R语言实战\\')
> set.seed(12345)
> x<-matrix(rnorm(n=100,mean=0,sd=1),ncol=2,byrow=TRUE)
> x[1:25,1]<-x[1:25,1]+3
> x[1:25,2]<-x[1:25,2]-4
> par(mfrow=c(2,2))
> plot(x,main="样本观测点的分布",xlab="",ylab="")
> KMClu1<-kmeans(x=x,centers=2,nstart = 1)
> points(KMClu1$centers,pch=3)
> set.seed(12345)
> (KMClu1<-kmeans(x=x,centers=2,nstart=1))
K-means clustering with 2 clusters of sizes 26, 24 每类的个数

Cluster means:  质心点
       [,1]       [,2]
1 3.1396595 -3.7636429
2 0.1718023  0.4841679

Clustering vector: 属于的类别
 [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 1 2 2 2 2 2 2 2
[38] 2 2 2 2 2 2 2 2 2 2 2 2 2

Within cluster sum of squares by cluster:
[1] 62.03865 52.05340
 (between_SS / total_SS =  74.6 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"      
> plot(x,col=(KMClu1$cluster+1),main="K-Means聚类K=2",xlab="",ylab="",pch=20,cex=1.5)
> points(KMClu1$centers,pch=3)
> set.seed(12345)
> KMClu2<-kmeans(x=x,centers=4,nstart=1)
> KMClu2
K-means clustering with 4 clusters of sizes 10, 15, 15, 10

Cluster means:
       [,1]      [,2]
1 3.1311572 -5.086319
2 3.2611523 -2.986441
3 0.1445016  1.329080
4 0.3358022 -1.051107

Clustering vector:
 [1] 2 1 1 1 1 2 2 2 1 2 2 1 4 2 1 2 2 2 1 2 1 2 2 2 1 3 3 3 3 2 4 3 4 3 4 4 3
[38] 3 4 3 3 3 3 4 3 4 4 3 3 4

Within cluster sum of squares by cluster:
[1]  9.294879 20.486878 15.382149 10.803772
 (between_SS / total_SS =  87.5 %)

Available components:

[1] "cluster"      "centers"      "totss"        "withinss"     "tot.withinss"
[6] "betweenss"    "size"         "iter"         "ifault"      
> plot(x,col=(KMClu2$cluster+1),main="K-Means聚类K=4,nstart=1",xlab="",ylab="",pch=20,cex=1.5)
> points(KMClu2$centers,pch=3)
> KMClu1$betweenss/(2-1)/KMClu1$tot.withinss/(50-2)
[1] 0.06119216
> KMClu2$betweenss/(4-1)/KMClu2$tot.withinss/(50-4)
[1] 0.05091425
> set.seed(12345)
> KMClu2<-kmeans(x=x,centers=4,nstart=30)
> plot(x,col=(KMClu2$cluster+1),main="K-Means聚类K=4,nstart=30",xlab="",ylab="",pch=20,cex=1.5)
> points(KMClu2$centers,pch=3)

从上面可以看出聚类为2类要优于4类

> #####################K-Means聚类应用
> PoData<-read.table("G:\\R语言\\大三下半年\\R语言数据挖掘方法及应用\\环境污染数据.txt",header=TRUE)
> CluData<-PoData[,2:7]
> #############K-Means聚类
> set.seed(12345)
> CluR<-kmeans(x=CluData,centers=4,iter.max=10,nstart=30)
> CluR$size 各列的样本量
[1]  2 19  4  6
> CluR$centers 类质心
        x1       x2       x3       x4       x5       x6
1 11.48000 79.47000 69.43000 59.88000 33.07000  9.62000
2 15.06895 15.09263 20.43263  5.31000 13.37316 16.45105
3 53.39250  8.33500  7.97000  1.42250 36.78750 83.69250
4 26.91000 39.77167 63.68333 10.42833 56.67667 40.70000

> ###########K-Means聚类结果的可视化 ####
> par(mfrow=c(2,1))
> PoData$CluR<-CluR$cluster
> plot(PoData$CluR,pch=PoData$CluR,ylab="类别编号",xlab="省市",main="聚类的类成员",axes=FALSE)
> par(las=2)
> axis(1,at=1:31,labels=PoData$province,cex.axis=0.6)
> axis(2,at=1:4,labels=1:4,cex.axis=0.6)
> box()
> legend("topright",c("第一类","第二类","第三类","第四类"),pch=1:4,cex=0.4)

 

 

###########K-Means聚类特征的可视化####
> plot(CluR$centers[1,],type="l",ylim=c(0,82),xlab="聚类变量",ylab="组均值(类质心)",main="各类聚类变量均值的变化折线图",axes=FALSE)
> axis(1,at=1:6,labels=c("生活污水排放量","生活二氧化硫排放量","生活烟尘排放量","工业固体废物排放量","工业废气排放总量","工业废水排放量"),cex.axis=0.6)
> box()
> lines(1:6,CluR$centers[2,],lty=2,col=2)
> lines(1:6,CluR$centers[3,],lty=3,col=3)
> lines(1:6,CluR$centers[4,],lty=4,col=4)
> legend("topleft",c("第一类","第二类","第三类","第四类"),lty=1:4,col=1:4,cex=0.3)

第二类的各类排放物排放量均不高；第一类主要是二氧化硫、烟尘和污水排放。

 

 ###########K-Means聚类效果的可视化评价####

#类间差异性
> CluR$betweenss/CluR$totss*100
[1] 64.92061

> par(mfrow=c(2,3))
> plot(PoData[,c(2,3)],col=PoData$CluR,main="生活污染情况",xlab="生活污水排放量",ylab="生活二氧化硫排放量")
> points(CluR$centers[,c(1,2)],col=rownames(CluR$centers),pch=8,cex=2)
> plot(PoData[,c(2,4)],col=PoData$CluR,main="生活污染情况",xlab="生活污水排放量",ylab="生活烟尘排放量")
> points(CluR$centers[,c(1,3)],col=rownames(CluR$centers),pch=8,cex=2)
> plot(PoData[,c(3,4)],col=PoData$CluR,main="生活污染情况",xlab="生活二氧化硫排放量",ylab="生活烟尘排放量")
> points(CluR$centers[,c(2,3)],col=rownames(CluR$centers),pch=8,cex=2)
> plot(PoData[,c(5,6)],col=PoData$CluR,main="工业污染情况",xlab="工业固体废物排放量",ylab="工业废气排放总量")
> points(CluR$centers[,c(4,5)],col=rownames(CluR$centers),pch=8,cex=2)
> plot(PoData[,c(5,7)],col=PoData$CluR,main="工业污染情况",xlab="工业固体废物排放量",ylab="工业废水排放量")
> points(CluR$centers[,c(4,6)],col=rownames(CluR$centers),pch=8,cex=2)
> plot(PoData[,c(6,7)],col=PoData$CluR,main="工业污染情况",xlab="工业废气排放总量",ylab="工业废水排放量")
> points(CluR$centers[,c(5,6)],col=rownames(CluR$centers),pch=8,cex=2)

从上图可以看出类质心位置较远

> #################PAM聚类####
> set.seed(12345)
> x<-matrix(rnorm(n=100,mean=0,sd=1),ncol=2,byrow=TRUE)
> x[1:25,1]<-x[1:25,1]+3
> x[1:25,2]<-x[1:25,2]-4
> library("cluster")
> set.seed(12345)

#聚成2类
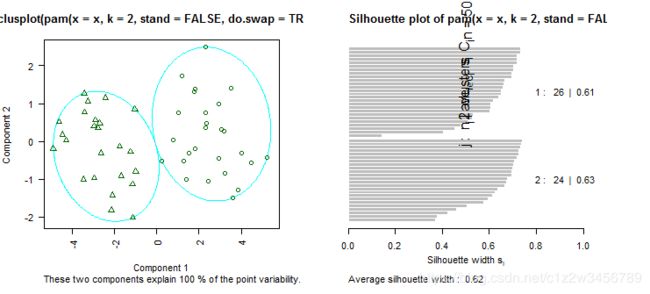
> (PClu<-pam(x=x,k=2,do.swap=TRUE,stand=FALSE))

ID是18，45为质心
Medoids:
     ID                     
[1,] 18 3.2542712 -3.5088117
[2,] 45 0.5365237  0.8248701
Clustering vector:
 [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 1 2 2 2 2 2 2 2
[38] 2 2 2 2 2 2 2 2 2 2 2 2 2
Objective function:
   build     swap 
1.721404 1.382137 

Available components:
 [1] "medoids"    "id.med"     "clustering" "objective"  "isolation" 
 [6] "clusinfo"   "silinfo"    "diss"       "call"       "data"      
> plot(x=PClu,data=x)

 

> ################层次聚类####
> PoData<-read.table("G:\\R语言\\大三下半年\\R语言数据挖掘方法及应用\\环境污染数据.txt",header=TRUE)
> CluData<-PoData[,2:7]

#计算欧式距离的距离矩阵
> DisMatrix<-dist(CluData,method="euclidean")

#采用ward法聚类聚类
> CluR<-hclust(d=DisMatrix,method="ward.D")

> ###############层次聚类的树形图
> par(mfrow=c(1,1))
> plot(CluR,labels=PoData[,1])
> box()

 

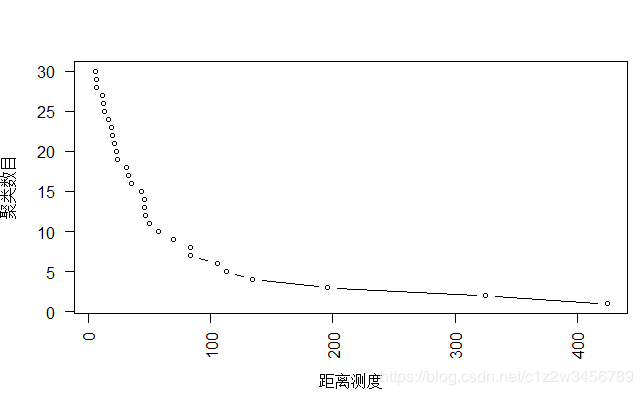
> ###########层次聚类的碎石图

当聚类我的数目为4时，最小的类间距离变大
> plot(CluR$height,30:1,type="b",cex=0.7,xlab="距离测度",ylab="聚类数目")

> PoData$memb<-cutree(CluR,k=4)
> table(PoData$memb) #查看各类的个数

 1  2  3  4 
 7  7 13  4 
> plot(PoData$memb,pch=PoData$memb,ylab="类别编号",xlab="省市",main="聚类的类成员",axes=FALSE)
> par(las=2)
> axis(1,at=1:31,labels=PoData$province,cex.axis=0.6)
> axis(2,at=1:4,labels=1:4,cex.axis=0.6)
> box()

 

> ##############混合高斯分布模拟
> library("MASS")
> set.seed(12345)
> mux1<-0
> muy1<-0
> mux2<-15
> muy2<-15
> ss1<-10
> ss2<-10
> s12<-3
> sigma<-matrix(c(ss1,s12,s12,ss2),nrow=2,ncol=2)
> Data1<-mvrnorm(n=100,mu=c(mux1,muy1),Sigma=sigma,empirical=TRUE)
> Data2<-mvrnorm(n=50,mu=c(mux2,muy2),Sigma=sigma,empirical=TRUE)
> Data<-rbind(Data1,Data2)
> plot(Data,xlab="x",ylab="y")

> library("mclust")
> DataDens<-densityMclust(data=Data)
fitting ...
  |====================================================================| 100%
> plot(x=DataDens,type="persp",col=grey(level=0.8),xlab="x",ylab="y")
Model-based density estimation plots: 

1: BIC
2: density

Selection: 1

Model-based density estimation plots: 

1: BIC
2: density

Selection: 2

 

 

> #########################对模拟数据的EM聚类
> library("mclust")
> EMfit<-Mclust(data=Data)
fitting ...
  |====================================================================| 100%
> summary(EMfit)
---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust EEE (ellipsoidal, equal volume, shape and orientation) model with 2
components: 

 log-likelihood   n df       BIC       ICL
       -857.359 150  8 -1754.803 -1755.007

Clustering table:
  1   2 
100  50 
> summary(EMfit,parameters=TRUE)
---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust EEE (ellipsoidal, equal volume, shape and orientation) model with 2
components: 

 log-likelihood   n df       BIC       ICL
       -857.359 150  8 -1754.803 -1755.007

Clustering table:
  1   2 
100  50 

Mixing probabilities:
        1         2 
0.6663218 0.3336782 

Means:
             [,1]     [,2]
[1,] -0.003082719 14.99065
[2,] -0.001821635 14.98813

Variances:
[,,1]
         [,1]     [,2]
[1,] 9.882603 2.988535
[2,] 2.988535 9.907798
[,,2]
         [,1]     [,2]
[1,] 9.882603 2.988535
[2,] 2.988535 9.907798
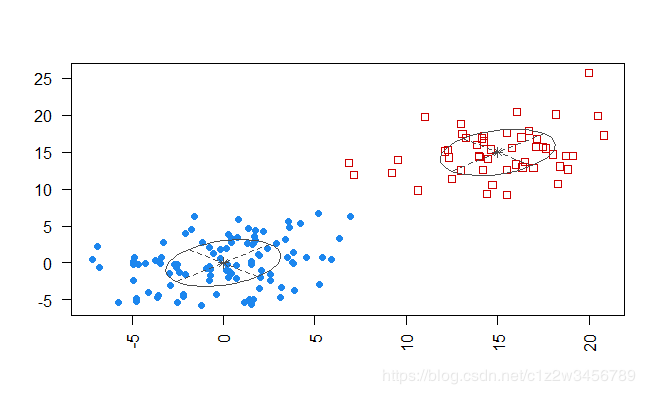
> plot(EMfit,"classification")

> plot(EMfit,"uncertainty")

> plot(EMfit,"density")

> #############通过mclustBIC函数实现EM聚类####
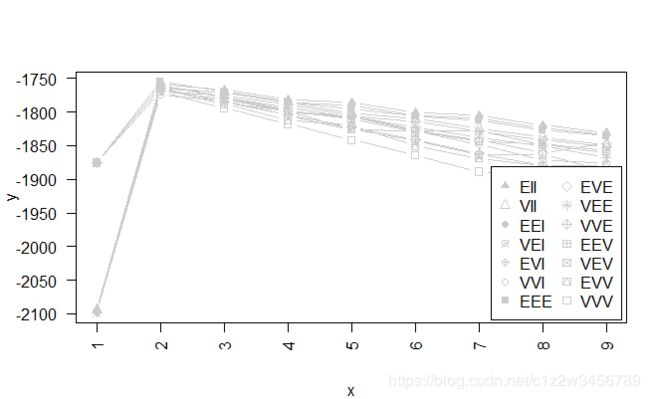
> (BIC<-mclustBIC(data=Data))
fitting ...
  |====================================================================| 100%
Bayesian Information Criterion (BIC): 
        EII       VII       EEI       VEI       EVI       VVI       EEE
1 -2094.031 -2094.031 -2099.042 -2099.042 -2099.042 -2099.042 -1875.167
2 -1759.047 -1764.056 -1764.057 -1769.067 -1769.068 -1774.078 -1754.803
3 -1766.466 -1771.095 -1771.425 -1775.296 -1780.141 -1784.259 -1769.936
4 -1781.325 -1785.885 -1786.321 -1789.199 -1800.291 -1804.991 -1784.362
5 -1785.772 -1802.284 -1790.456 -1805.910 -1808.097 -1826.468 -1795.230
6 -1800.986 -1810.091 -1805.522 -1813.980 -1827.329 -1827.818 -1806.554
7 -1804.678 -1824.885 -1808.846 -1828.499 -1828.336 -1849.130 -1812.038
8 -1819.566 -1837.494 -1823.870 -1841.105 -1848.896 -1871.337 -1826.794
9 -1830.704 -1849.012 -1833.906 -1851.974 -1860.797 -1876.086 -1835.437
        EVE       VEE       VVE       EEV       VEV       EVV       VVV
1 -1875.167 -1875.167 -1875.167 -1875.167 -1875.167 -1875.167 -1875.167
2 -1759.811 -1759.813 -1764.822 -1759.814 -1764.824 -1764.822 -1769.832
3 -1778.629 -1778.475 -1785.531 -1777.426 -1785.714 -1787.933 -1794.073
4 -1798.275 -1793.341 -1803.981 -1797.493 -1798.500 -1812.765 -1817.697
5 -1806.244 -1807.094 -1822.240 -1810.194 -1826.262 -1820.228 -1841.491
6 -1827.120 -1822.126 -1841.689 -1829.354 -1842.631 -1850.272 -1864.515
7 -1842.140 -1838.001 -1862.351 -1843.656 -1863.670 -1868.964 -1888.643
8 -1861.053 -1850.279 -1879.266 -1847.211 -1863.402 -1880.443 -1897.018
9 -1846.870 -1868.095 -1897.053 -1857.843 -1887.633 -1878.911        NA

Top 3 models based on the BIC criterion: 
    EEE,2     EII,2     EVE,2 
-1754.803 -1759.047 -1759.811 
> plot(BIC,G=1:7,col="black")

> (BICsum<-summary(BIC,data=Data))
Best BIC values:
             EEE,2       EII,2        EVE,2
BIC      -1754.803 -1759.04658 -1759.811202
BIC diff     0.000    -4.24341    -5.008037

Classification table for model (EEE,2): 

  1   2 
100  50 
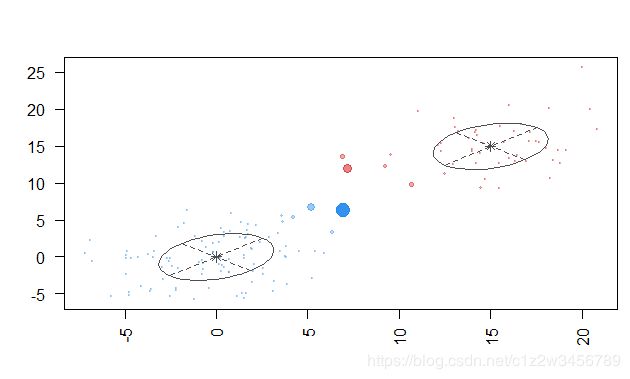
> mclust2Dplot(Data,classification=BICsum$classification,parameters=BICsum$parameters)

> ###################实例数据的EM聚类####
> PoData<-read.table("G:\\R语言\\大三下半年\\R语言数据挖掘方法及应用\\环境污染数据.txt",header=TRUE)
> CluData<-PoData[,2:7]
> library("mclust")
> EMfit<-Mclust(data=CluData)
fitting ...
  |====================================================================| 100%
> summary(EMfit)
---------------------------------------------------- 
Gaussian finite mixture model fitted by EM algorithm 
---------------------------------------------------- 

Mclust EEV (ellipsoidal, equal volume and shape) model with 5 components: 

 log-likelihood  n  df       BIC       ICL
      -542.7661 31 115 -1480.441 -1480.441

Clustering table:
1 2 3 4 5 
6 8 5 7 5 
> plot(EMfit,"BIC")

> plot(EMfit,"classification")