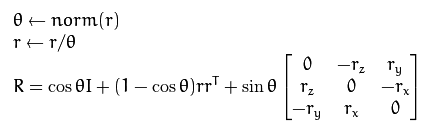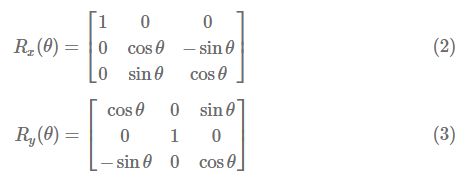三维坐标系旋转——旋转矩阵到旋转角之间的换算

相关文章：

matlab相机标定获取内参

旋转矩阵到旋转角之间的换算

solvepnp 单目三维位姿估计--------利用二维码求解相机世界坐标

solvepnp 单目三维位姿估计--------理论

 

在做单目三维位姿估计（即估计目标物相对相机的姿态或相机相对目标物的姿态）时会用到solvepnp函数，

函数原型为：

cv2.solvePnP(objectPoints, imagePoints, cameraMatrix, distCoeffs[, rvec[, tvec[, useExtrinsicGuess[, flags]]]]) → retval, rvec, tvec

参数解释

• objectPoints：世界坐标系中的3D点坐标，单位mm

• imagePoints：图像坐标系中点的坐标，单位像素

• cameraMatrix：相机内参矩阵

• distCoeffs：畸变系数

• rvec：旋转矩阵

• tvec：平移矩阵

• useExtrinsicGuess：是否输出平移矩阵和旋转矩阵，默认为false

• flags：SOLVEPNP _ITERATIVE、SOLVEPNP _P3P、SOLVEPNP _EPNP、SOLVEPNP _DLS、SOLVEPNP _UPNP

内参矩阵和畸变系数都是要通过标定得到的，这个不细讲，opencv官方提供了有标定例子（或者参考我的这篇文章：用matlab标定获取相机内参矩阵和畸变系数）。函数输出的是旋转矩阵rvec和tvec。

 

本文就来说说得到了这个旋转矩阵rvec后，如何得知目标物实际的角度呢~

---

旋转矩阵是一个3×3的正交矩阵，有3个自由度。处理旋转矩阵的问题时，通常采用旋转矩阵的方式来描述，也可以用旋转向量来表示，两者之间可以通过罗德里格斯（Rodrigues）变换来进行转换。

旋转矩阵和旋转向量间的转换请参考：旋转矩阵 和 旋转向量

其中，旋转向量的长度（模）表示绕轴逆时针旋转的角度（弧度）。

norm为求向量的模。

代码如下：

theta = np.linalg.norm(rvec)
r = rvec / theta
R_ = np.array([[0, -r[2][0], r[1][0]],
               [r[2][0], 0, -r[0][0]],
               [-r[1][0], r[0][0], 0]])
R = np.cos(theta) * np.eye(3) + (1 - np.cos(theta)) * r * r.T + np.sin(theta) * R_
print('旋转矩阵')
print(R)

反变换也可以很容易的通过如下公式实现：

---

空间中三维坐标变换一般由三种方式实现，第一种是旋转矩阵和旋转向量；第二种是欧拉角；第三种是四元数。下面介绍旋转矩阵(旋转向量)与欧拉角实现三维空间坐标变换的方法以及两者之间的关系。

 

旋转矩阵

对于一个三维空间的点 P(x,y,z)P(x,y,z)，要将其绕 zz 轴旋转 θθ 角度是可以很简单地用旋转矩阵来表示的

 欧拉角

 

 此处得到结论：自旋转的“先转的放前面”

---

定角（Fixed angles）

围绕固定的坐标系转动。固定坐标系的原点，坐标系再围绕已经固定的轴转动，全程原坐标系不动。

注意！移动位置的顺序可以调换，但是旋转的顺序不能调换，结果不一样。

以X-Y-Z型为例子：即先围绕X轴进行转动γ°，然后围绕Y轴进行转动β°，最后围绕Z轴进行转动α°。注意逆时针为正方向。

X-Y-Z型公式：

重点：先转的轴的放后面运算，如下

代码：

def isRotationMatrix(R):
    Rt = np.transpose(R)   #旋转矩阵R的转置
    shouldBeIdentity = np.dot(Rt, R)   #R的转置矩阵乘以R
    I = np.identity(3, dtype=R.dtype)           # 3阶单位矩阵
    n = np.linalg.norm(I - shouldBeIdentity)   #np.linalg.norm默认求二范数
    return n < 1e-6                            # 目的是判断矩阵R是否正交矩阵（旋转矩阵按道理须为正交矩阵，如此其返回值理论为0）


def rotationMatrixToAngles(R):
    assert (isRotationMatrix(R))   #判断是否是旋转矩阵（用到正交矩阵特性）

    sy = math.sqrt(R[0, 0] * R[0, 0] + R[1, 0] * R[1, 0])  #矩阵元素下标都从0开始（对应公式中是sqrt(r11*r11+r21*r21)），sy=sqrt(cosβ*cosβ)

    singular = sy < 1e-6   # 判断β是否为正负90°

    if not singular:   #β不是正负90°
        x = math.atan2(R[2, 1], R[2, 2])
        y = math.atan2(-R[2, 0], sy)
        z = math.atan2(R[1, 0], R[0, 0])
    else:              #β是正负90°
        x = math.atan2(-R[1, 2], R[1, 1])
        y = math.atan2(-R[2, 0], sy)   #当z=0时，此公式也OK，上面图片中的公式也是OK的
        z = 0

    return np.array([x, y, z])

 备注：np.linalg.norm(求范数)

 举例：

由角度推旋转矩阵

由旋转矩阵推角度

 

---

欧拉角（Euler angles）

“自旋转”，围绕当下（自己）的坐标系某轴转动，就是每次旋转，都固定被围绕的某一轴，另两轴动。

每次旋转，整个坐标系都会改变位置。

以Z-Y-Z型为例的公式：

重点：先转的轴的放前面运算，如下

举例：

矩阵转角度:

注意：自旋转的“先转的放前面”

---

欧拉角转旋转矩阵 

欧拉角通过将刚体绕过原点的轴(i,j,k)旋转θ，分解成三步，如下图（蓝色是起始坐标系，而红色的是旋转之后的坐标系） 
 
如果将每一个角度用旋转矩阵表示如下： 
 
所以，容易得到，欧拉角转旋转矩阵如下：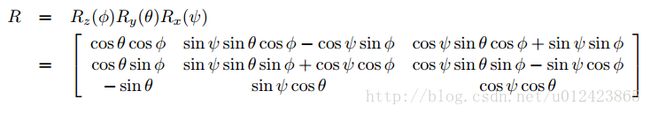 

代码：

/**
欧拉角计算对应的旋转矩阵
**/
Mat eulerAnglesToRotationMatrix(Vec3f &theta)
{
    // 计算旋转矩阵的X分量
    Mat R_x = (Mat_(3,3) <<
               1,       0,              0,
               0,       cos(theta[0]),   -sin(theta[0]),
               0,       sin(theta[0]),   cos(theta[0])
               );
 
 
    // 计算旋转矩阵的Y分量
    Mat R_y = (Mat_(3,3) <<
               cos(theta[1]),    0,      sin(theta[1]),
               0,               1,      0,
               -sin(theta[1]),   0,      cos(theta[1])
               );
 
 
    // 计算旋转矩阵的Z分量
    Mat R_z = (Mat_(3,3) <<
               cos(theta[2]),    -sin(theta[2]),      0,
               sin(theta[2]),    cos(theta[2]),       0,
               0,               0,                  1);
 
 
    // 合并 
    Mat R = R_z * R_y * R_x;
 
 
    return R;
}

 

---

 旋转矩阵转欧拉角 

将旋转矩阵表示如下： 
 
则可以如下表示欧拉角： 

代码：

/**
 * 功能： 1. 检查是否是旋转矩阵
**/
bool isRotationMatrix(Mat &R)
{
    Mat Rt;
    transpose(R, Rt);
    Mat shouldBeIdentity = Rt * R;
    Mat I = Mat::eye(3,3, shouldBeIdentity.type());

    return  norm(I, shouldBeIdentity) < 1e-6;    
}

/**
 * 功能： 1. 通过给定的旋转矩阵计算对应的欧拉角
**/
Vec3f rotationMatrixToEulerAngles(Mat &R)
{
    assert(isRotationMatrix(R));

    float sy = sqrt(R.at(0,0) * R.at(0,0) +  R.at(1,0) * R.at(1,0) );

    bool singular = sy < 1e-6; // If

    float x, y, z;
    if (!singular) {
        x = atan2(R.at(2,1) , R.at(2,2));
        y = atan2(-R.at(2,0), sy);
        z = atan2(R.at(1,0), R.at(0,0));
    } else {
        x = atan2(-R.at(1,2), R.at(1,1));
        y = atan2(-R.at(2,0), sy);
        z = 0;
    }
    return Vec3f(x, y, z);   
}

旋转向量转欧拉角（经过四元数）代码如下：

# 从旋转向量转换为欧拉角
def get_euler_angle(rotation_vector):
    # calculate rotation angles
    theta = cv2.norm(rotation_vector, cv2.NORM_L2)
    
    # transformed to quaterniond
    w = math.cos(theta / 2)
    x = math.sin(theta / 2)*rotation_vector[0][0] / theta
    y = math.sin(theta / 2)*rotation_vector[1][0] / theta
    z = math.sin(theta / 2)*rotation_vector[2][0] / theta
    
    ysqr = y * y
    # pitch (x-axis rotation)
    t0 = 2.0 * (w * x + y * z)
    t1 = 1.0 - 2.0 * (x * x + ysqr)
    print('t0:{}, t1:{}'.format(t0, t1))
    pitch = math.atan2(t0, t1)
    
    # yaw (y-axis rotation)
    t2 = 2.0 * (w * y - z * x)
    if t2 > 1.0:
        t2 = 1.0
    if t2 < -1.0:
        t2 = -1.0
    yaw = math.asin(t2)
    
    # roll (z-axis rotation)
    t3 = 2.0 * (w * z + x * y)
    t4 = 1.0 - 2.0 * (ysqr + z * z)
    roll = math.atan2(t3, t4)
    
    print('pitch:{}, yaw:{}, roll:{}'.format(pitch, yaw, roll))
    
	# 单位转换：将弧度转换为度
    Y = int((pitch/math.pi)*180)
    X = int((yaw/math.pi)*180)
    Z = int((roll/math.pi)*180)
    
    return 0, Y, X, Z

在3D 空间中，表示物体的旋转可以由三个欧拉角来表示： 
pitch围绕X轴旋转，叫俯仰角。 
yaw围绕Y轴旋转，叫偏航角。 
roll围绕Z轴旋转，叫翻滚角。 
这三个角的顺序对旋转结果有影响。 

（欧拉角与四元数的转换关系： 
http://www.cnblogs.com/wqj1212/archive/2010/11/21/1883033.html）

四元数到欧拉角的转换公式如下： 
  
arctan和arcsin的结果为[-pi/2,pi/2]，不能覆盖所有的欧拉角，因此采用atan2代替arctan： 

 

 

 

参考：http://blog.miskcoo.com/2016/12/rotation-in-3d-space

https://blog.csdn.net/aic1999/article/details/82415357#commentBox

https://www.cnblogs.com/aoru45/p/9781540.html

https://blog.csdn.net/u012423865/article/details/78219787#commentsedit

https://blog.csdn.net/u013512448/article/details/77804161