EBGAN, LSGAN, BEGAN

本文主要对EBGAN, LSGAN, BEGAN三个模型核心理论进行简单记录．

引言　　

GAN的原理就是利用Discriminator作为Generator的引导，使得最终Generator生成的samples可以以假乱真，具体过程可以用下图表示．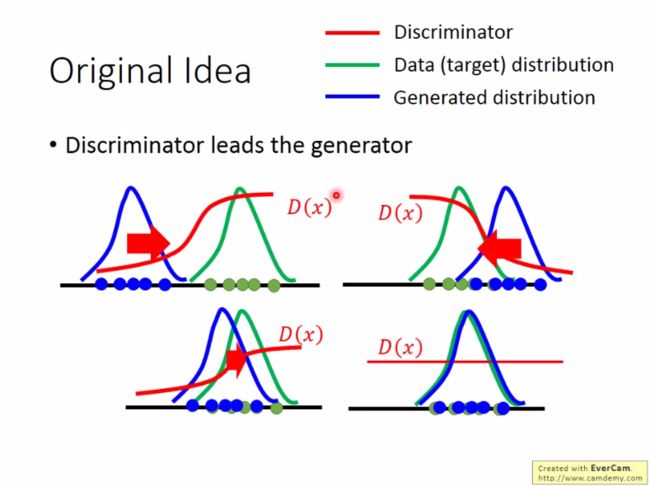　　
上图来自李宏毅深度学习PPT中，蓝色线表示Generator distribution, 绿色线表示data distribution,在优化过程中，对于real data我们 要使得最后的prob接近1,fake data最后的损失接近0,那么这个优化过程会使得G向real data的分布靠近，因为real data分布可以使得最后discriminator 的预测最大，当跑过头然后再往回更新，最终达到制衡．此时generator得到的samples与real data分布相近．　　

以上是最为常见的GAN的做法，最后的evaluation function是binary classification,那这篇Post主要讲的GAN可以看作为enegry-based. 那么能量的度量与 分类相反，当两个分布接近的时候，能量达到平衡，也就是最小，可以看作classification-based GAN损失函数取反．我们首先来看看EBGAN.

EBGAN1

EBGAN网络结构如下图表示：　　

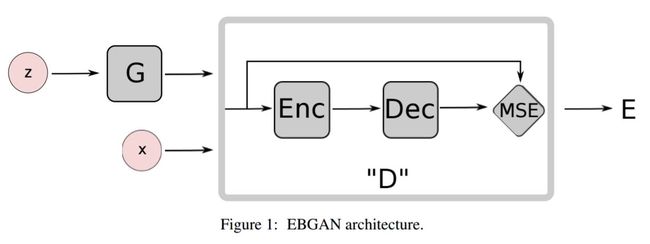
上图中，discriminator与以往的GAN不同，使用的结构为AutoEncoder, 这样的结构输入是Image, 输出也是image, 因此为了度量fake or real,这里选取了MSE最为损失函数． 同时，加入margin．如下面公式表示：　　

LDx,z=D(x)+max(0,m−D(G(z)))LDx,z=D(x)+max(0,m−D(G(z)))

LGz=D(G(z))LGz=D(G(z))

上述都是最小化损失函数．对于real data, 在网络的输出我们得到对应的restruction loss, 如果用GAN原理来解释，可以看作generator的outputs输入到discriminator中，我们为 达到以假乱真，那么mse向较小的的方向更新，即此时G的分布应该趋近Data的分布. D的任务就是将这两种样本区分开．但这里有个缺点，就是real data的重构损失可以很小，最小到0,但 对于fake data,最大可以大到多大，无穷大，这对训练整个模型是不利的．因此引入margin, 由公式可以看出，引入margin之后，当D(G(z))D(G(z))大于m的时候，它对LDLD的贡献为0,可以 理解为对于偏离太离谱的fake data直接忽略． 如此一来，当G生产的data distribution接近real data时，两者重构损失是接近的，因此LDLD接近m, 此时mse在[0, m]之间．这说明引入margin之后 对于训练是有帮助的，而且可以使得G生产的data重构误差可以很小，自然可以解释为生成了可以看的图片．　　

这里考虑极端情况，如果D(x)+m−D(G(x))≈0D(x)+m−D(G(x))≈0,即D(x)−D(G(x))=−mD(x)−D(G(x))=−m,这时G的重构误差小于D,这种情况会不会出现．由GAN的对抗训练，是不会出现的．因为如果G的重构误差比real data重构误差还小，那么discriminator的引导作用消失，因为G的最终目标是real data的分布, 因此两者极端情况就是相等．　　

后续，作者为了增加样本多样性，利用code做文章，加入相似性的约束，这里主要对损失函数进行解读，可能有人会问margin可不可以自适应，可以的，MAGAN(Margin Adaptivation GAN),下面这篇GAN也可以看成自适应marginGAN.

LS-GAN2

同样的，先上公式：　　

LD(x,z)=D(x)+max(0,Δ(x,G(x))+D(x)−D(G(z)))LD(x,z)=D(x)+max(0,Δ(x,G(x))+D(x)−D(G(z)))

LG(z)=D(G(z))LG(z)=D(G(z))

上面公式如何理解，我们可以用下图来说明：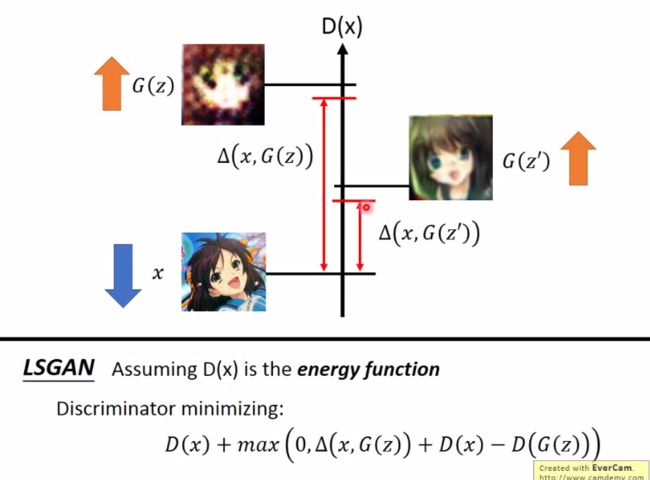　　
在优化时，margin=Δ(x,G(x))+D(x)margin=Δ(x,G(x))+D(x), 自适应反映在第一项．baseline为D(x)D(x),每次优化的margin为G生产的图片和real data之间的差异，这个差异可以使用mse等度量函数．当两者差异较大是margin就会很大，当随着优化的进行，两者差异会减小，此时二者margin就会很小．当达到理想情况，即G得到的data distribution接近real data,此时两者margin是此时discriminator对real data的重构损失，与D(G(z))D(G(z))很接近，此时LDLD达到理想的最小值．　　 LS-GAN较EBGAN优点在于margin自适应，当然可以看作EBGAN的一种．　　

BEGAN3

直接上公式：　　

LD(x,z)=D(x)－ktD(G(z))LD(x,z)=D(x)－ktD(G(z))

LG(z)=D(G(z))LG(z)=D(G(z))

其中ktkt初始化为0,即D在训练最开始只针对real data进行建模，直到满足D(x)D(x)大于D(G(z))D(G(z)),也就是不能让G生产的数据被认为是real data.目标还是使得G最后的分布接近real data,但不能超越real data.整个训练过程相当于以逸待劳，每次当满足上述条件时，更新ktkt, 然后在下一次满足条件是再次更新，这样可以达到逐步迁移分布的效果．更新公式如下：　　

kt+1=kt+λ(γD(x)−D(G(z)))kt+1=kt+λ(γD(x)−D(G(z)))

γγ的值可以设置，可以设想一下，如果γγ的不断减小逼近0,那么最后G得到的图片可以看成real data,因为此时一直在更新ktkt.

下图是实验结果：　　

这里BEGAN结构使用与EBGAN相同，不同之处在于loss function的设计，可以看到,BEGAN生成的图片有点厉害.

这篇post就到这里，主要讲Enegry-based GAN以及margin的GAN的损失函数,没有对模型具体细节进行探讨，具体还需参看论文.

References

1. Zhao J, Mathieu M, Lecun Y. Energy-based Generative Adversarial Network[J]. 2017. ↩

2. Qi G J. Loss-Sensitive Generative Adversarial Networks on Lipschitz Densities[J]. 2017. ↩

3. Boundary Equilibrium Generative Adversarial Networks ↩