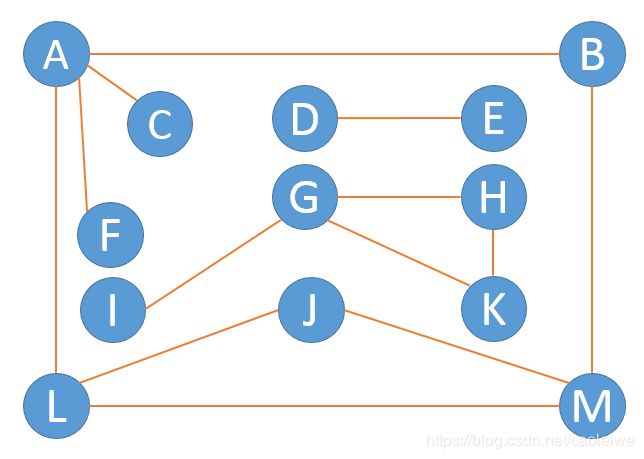
无向图的连通分量和生成树

     以下内容主要参考于严蔚敏版的数据结构教材。
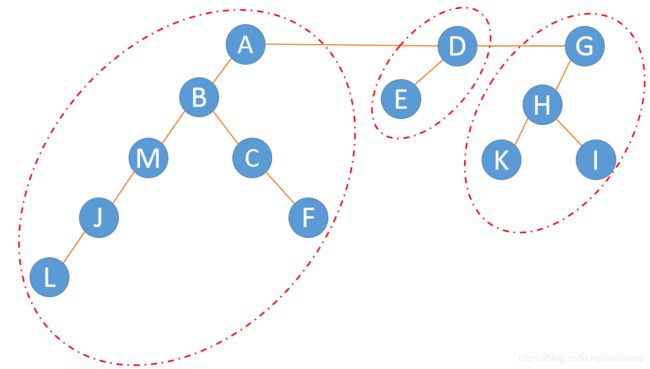
     以下算法生成无向图的深度优先生成森林，图采用邻接表数据结构，生成森林才有左孩子右兄弟的存储结构。无向图的深度优先生成树或森林其实就是从图中某一个顶点V的深度优先遍历过程。将当前节点第一个邻接点作为其左孩子元素，第一个兄弟作为其右兄弟元素（如果当前节点为节点V且图不是连通图，则节点V的右兄弟元素为第二颗生成树的根节点，第二颗生成树的右兄弟元素为第三颗生成树的根节点，以此类推）。图1的非连通图的孩子兄弟节点结构的生成森林如图2所示。无向图的广度优先生成树与生成森林与此类似。

　 图1.

　 图2.

//图的邻接表表示
//弧节点
class GraphArcNode
{
private:
	int weight;
	int adjVertexIndex;
	GraphArcNode* nextArcNode;
public:
	GraphArcNode(int d = 0, int index = 0)
	{
		weight = d;
		adjVertexIndex = index;
		nextArcNode = nullptr;
	}
	void setNextArcNode(GraphArcNode* next)
	{
		nextArcNode = next;
	}
	int getWeight()
	{
		return weight;
	}
	int getAdjVertexIndex()
	{
		return adjVertexIndex;
	}
	GraphArcNode* getNextArcNode()
	{
		return nextArcNode;
	}
};
//图节点
class GraphNode
{
private:
	int data;
	GraphArcNode* nextArcNode;
public:
	GraphNode(int d = 0)
	{
		data = d;
		nextArcNode = nullptr;
	}
	void setNextArcNode(GraphArcNode* next)
	{
		nextArcNode = next;
	}
	int getData()
	{
		return data;
	}
	GraphArcNode* getNextArcNode()
	{
		return nextArcNode;
	}
};
//图的数据结构
class ALGraph
{
private:
	vector<GraphNode> graphNodeSet;
	int nodeNum;
public:
	ALGraph(int num)
	{
		nodeNum = num;
	}
	void addGraphNode(int data)
	{
		graphNodeSet.push_back(GraphNode(data));
	}
	int getGraphNodeNum()
	{
		return nodeNum;
	}
	vector<GraphNode> getGraphNodeSet()
	{
		return graphNodeSet;
	}
	void setGraphNodeArc(int graphNodeIndex, int weight, int adjVertexIndex)
	{
		if (graphNodeSet[graphNodeIndex].getNextArcNode() == nullptr)
		{
			graphNodeSet[graphNodeIndex].setNextArcNode(new GraphArcNode(weight, adjVertexIndex));
		}
		else
		{
			GraphArcNode* currentArcNode = graphNodeSet[graphNodeIndex].getNextArcNode();
			GraphArcNode* nextArcNode = graphNodeSet[graphNodeIndex].getNextArcNode()->getNextArcNode();
			while (nextArcNode != nullptr)
			{
				currentArcNode = nextArcNode;
				nextArcNode = nextArcNode->getNextArcNode();
			}
			currentArcNode->setNextArcNode(new GraphArcNode(weight, adjVertexIndex));
		}
	}
};

class CSNode
{
private:
	int data;
	CSNode* leftChild;
	CSNode* rightBrother;
public:
	CSNode(int d=0,CSNode* left = nullptr, CSNode* right=nullptr)
	{
		data = d;
		leftChild = nullptr;
		rightBrother = nullptr;
	}

	void setData(int value)
	{
		data = value;
	}
	void setLeft(CSNode* value)
	{
		leftChild = value;
	}
	void setRight(CSNode* value)
	{
		rightBrother = value;
	}

	int getData()
	{
		return data;
	}

	CSNode* getLeft()
	{
		return leftChild;
	}
	CSNode* getRight()
	{
		return rightBrother;
	}
};




int findNextAdjNodeIndex(ALGraph g, int currentNodeIndex, vector<bool>& visited)
{

	if (currentNodeIndex >= 0)
	{
		GraphArcNode* currentArcNode = g.getGraphNodeSet()[currentNodeIndex].getNextArcNode();
		while ((currentArcNode != nullptr) && (visited[currentArcNode->getAdjVertexIndex()]))
		{
			currentArcNode = currentArcNode->getNextArcNode();
		}

		if (currentArcNode != nullptr)
		{
			return currentArcNode->getAdjVertexIndex();
		}
		else
		{
			return -1;
		}
	}
	return -1;
}


void DFSTree(ALGraph g, int nodeIndex,CSNode*& root, vector<bool> &visited)
{
	visited[nodeIndex] = true;
	cout << "nodeIndex=" << nodeIndex << endl;
	bool firstAdjVex = true;
	CSNode* before = nullptr;
	for (int adjVexIndex=findNextAdjNodeIndex(g, nodeIndex, visited);adjVexIndex>=0; adjVexIndex= findNextAdjNodeIndex(g, nodeIndex, visited))
	{
		if (!visited[adjVexIndex])
		{

			CSNode* p = new CSNode(g.getGraphNodeSet()[adjVexIndex].getData(), nullptr, nullptr);
			if (firstAdjVex)
			{
				root->setLeft(p);
				firstAdjVex = false;
			}
			else
			{
				cout << "right data=" << p->getData() << endl;
				before->setRight(p);
			}
			before = p;
			DFSTree(g, adjVexIndex, before, visited);
		}
	}

}

void DFSForest(ALGraph g, CSNode* &root)
{
	vector<bool> visited(g.getGraphNodeNum(), false);
	CSNode* before = nullptr;
	for (int nodeIndex = 0; nodeIndex < g.getGraphNodeNum(); nodeIndex++)
	{
		if (!visited[nodeIndex])
		{
			cout << "//// Tree start ////"<< endl;
			CSNode *p= new CSNode(g.getGraphNodeSet()[nodeIndex].getData(),nullptr,nullptr);
			if (root == nullptr)
				root = p;
			else
				before->setRight(p);
			before = p;
			DFSTree(g, nodeIndex, p, visited);
		}
	}

}


void printForest(CSNode* root)
{
	if (root != nullptr)
	{
		cout << "visiting node " << root->getData() << endl;
		printForest(root->getLeft());
		printForest(root->getRight());
	}
}

#define A 0
#define B 1
#define C 2
#define D 3
#define E 4 
#define F 5
#define G 6 
#define H 7
#define I 8
#define J 9
#define K 10
#define L 11
#define M 12



//测试程序
int main()
{
	ALGraph g(13);
	for (int nodeDataIndex = 0; nodeDataIndex < 13; nodeDataIndex++)
	{
		g.addGraphNode(nodeDataIndex);
	}
	g.setGraphNodeArc(A, 0, B);
	g.setGraphNodeArc(A, 0, C);
	g.setGraphNodeArc(A, 0, F);
	g.setGraphNodeArc(A, 0, L);
	g.setGraphNodeArc(B, 0, A);
	g.setGraphNodeArc(B, 0, M);
	g.setGraphNodeArc(C, 0, A);
	g.setGraphNodeArc(D, 0, E);
	g.setGraphNodeArc(E, 0, D);
	g.setGraphNodeArc(F, 0, A);
	g.setGraphNodeArc(G, 0, H);
	g.setGraphNodeArc(G, 0, I);
	g.setGraphNodeArc(G, 0, K);
	g.setGraphNodeArc(H, 0, G);
	g.setGraphNodeArc(H, 0, K);
	g.setGraphNodeArc(I, 0, G);
	g.setGraphNodeArc(J, 0, L);
	g.setGraphNodeArc(J, 0, M);
	g.setGraphNodeArc(K, 0, G);
	g.setGraphNodeArc(K, 0, H);
	g.setGraphNodeArc(L, 0, A);
	g.setGraphNodeArc(L, 0, J);
	g.setGraphNodeArc(L, 0, M);
	g.setGraphNodeArc(M, 0, B);
	g.setGraphNodeArc(M, 0, J);
	g.setGraphNodeArc(M, 0, L);
	CSNode* root = nullptr;
	DFSForest(g, root);
	printForest(root);

}

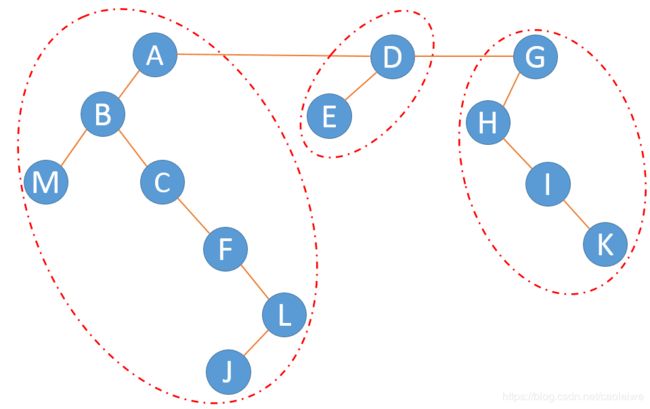
     图1的广度优先生成树如图3所示。

　 图3.

void findBeforeNode(CSNode* root,int nodeData, CSNode* &beforeNode)
{
	CSNode* left = root->getLeft();
	CSNode* right = root->getRight();
	if ((root!=nullptr)&&(root->getData() == nodeData))
	{
		beforeNode= root;
	}
	if (left != nullptr)
	{
		findBeforeNode(left, nodeData, beforeNode);
	}

	if (right != nullptr)
	{
		findBeforeNode(right, nodeData, beforeNode);
	}
}

void BFSForest(ALGraph g,CSNode*& root)
{
	vector<bool> visited(g.getGraphNodeNum(), false);
	queue<int> adjNode;
	CSNode* beforeTree = nullptr;
	int queueHead = 0;
	int nextAdjNodeIndex = 0;
	bool firstAdjNode = false;
	CSNode* beforeNode = nullptr;
	for (int i = 0; i < g.getGraphNodeNum(); i++)
	{
		if (!visited[i])
		{
			cout << "//// Tree start ////" << endl;
			CSNode* p1 = new CSNode(g.getGraphNodeSet()[i].getData(), nullptr, nullptr);
			cout << "root=" << p1 ->getData()<<endl;
			if (root == nullptr)
				root = p1;
			else
				beforeTree->setRight(p1);
			beforeTree = p1;
			visited[i] = true;
			adjNode.push(i);
			printForest(root);
			while (!adjNode.empty())
			{			
				queueHead = adjNode.front();
			    cout<<"queueHead = "<<queueHead<<endl;
				adjNode.pop();

				findBeforeNode(root, queueHead, beforeNode);
				cout << "beforeNode->getData=" << beforeNode->getData() << endl;
				firstAdjNode = true;
				//依次访问以前访问过的一个节点的所有邻接点
				for (GraphArcNode* nextAdjNode = g.getGraphNodeSet()[queueHead].getNextArcNode(); nextAdjNode != nullptr; nextAdjNode = nextAdjNode->getNextArcNode())
				{
					nextAdjNodeIndex = nextAdjNode->getAdjVertexIndex();
					if (!visited[nextAdjNodeIndex])
					{
						visited[nextAdjNodeIndex] = true;
						CSNode* p2 = new CSNode(g.getGraphNodeSet()[nextAdjNodeIndex].getData(), nullptr, nullptr);
						cout << "Adj data=" << g.getGraphNodeSet()[nextAdjNodeIndex].getData() << endl;
						if (firstAdjNode)
						{
							cout << "beforeNode->setLeft(p2);" << endl;
							beforeNode->setLeft(p2);
							firstAdjNode = false;
						}
						else
						{
							beforeNode->setRight(p2);
							cout << "beforeNode->setRight(p2);" << endl;
						}
						beforeNode = p2;
						adjNode.push(nextAdjNodeIndex);
					}
				}
			}
		}
	}
	return;
}