IEEE极限编程之The pipeline-动态规划思想

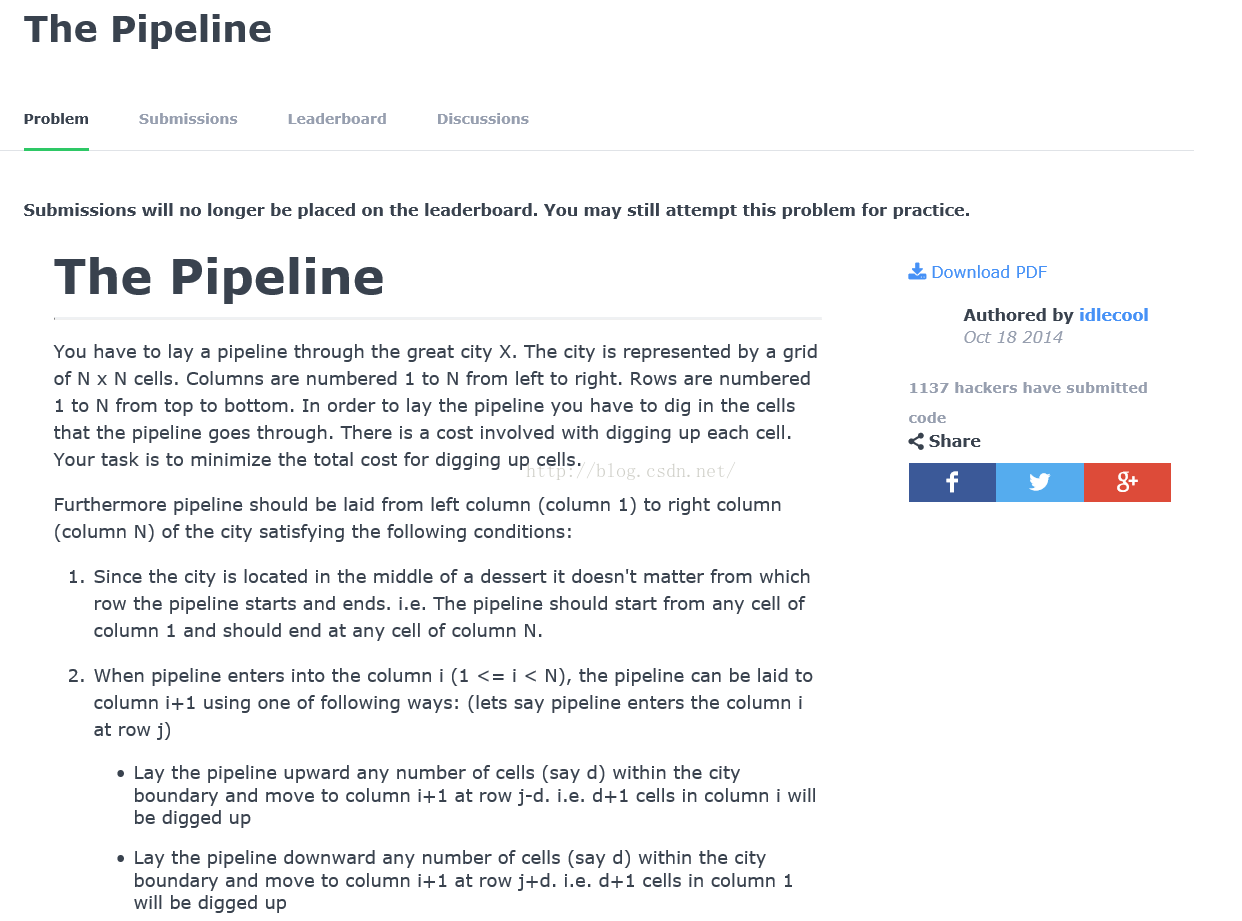
题目：

代码：

#include
#include
#include
#define NUM 100
using namespace std;

class solution{
public:
	void search_route(int cost[][NUM], int num[][NUM]){
		result.second.clear();
		int min = INT_MAX, row, column = NUM - 1, temp;
		for (int i = 0; i < NUM; i++){
			if (cost[i][NUM - 1] < min){
				min = cost[i][NUM - 1];
				row = i;//最小cost的行数
			}
		}
		result.first = min;
		result.second.push_back(make_pair(row, column));
		while (column != 0){
			bool flag = false;
			temp = cost[row][column] - num[row][column];
			if (row - 1 >= 0 && flag == false){//向上移动
				if (temp == cost[row - 1][column]){
					row -= 1;
					result.second.push_back(make_pair(row, column));
					flag = true;

				}
			}
			if (column - 1 >= 0 && flag == false){//向左移动
				if (temp == cost[row][column - 1]){
					column -= 1;
					result.second.push_back(make_pair(row, column));
					flag = true;
				}
			}
			if (row + 1>>The_pipeline(int num[][NUM], int cost[][NUM], int row, int column){//开始坐标
		list>que;
		if (cost[row][column] > num[row][column]){
			cost[row][column] = num[row][column];
			que.push_back(make_pair(row, column));
		}
		list>::iterator iter = que.begin();
		int temp;
		while (iter != que.end()){
			//能否向上移动
			if (iter->first - 1 >= 0){
				temp = cost[iter->first][iter->second] + num[iter->first - 1][iter->second];
				if (temp < cost[iter->first - 1][iter->second]){
					que.push_back(make_pair(iter->first - 1, iter->second));
					cost[iter->first - 1][iter->second] = temp;
				}
			}

			//能否右移动
			if (iter->second + 1 < NUM){
				temp = cost[iter->first][iter->second] + num[iter->first][iter->second + 1];
				if (temp < cost[iter->first][iter->second + 1]){
					que.push_back(make_pair(iter->first, iter->second + 1));
					cost[iter->first][iter->second + 1] = temp;
				}
			}

			//能否向下移动
			if (iter->first + 1 < NUM){
				temp = cost[iter->first][iter->second] + num[iter->first + 1][iter->second];
				if (temp < cost[iter->first + 1][iter->second]){
					que.push_back(make_pair(iter->first + 1, iter->second));
					cost[iter->first + 1][iter->second] = temp;
				}
			}
			iter++;
		}
		search_route(cost, num);
		return result;
	}
	pair>>result;
};

int main(){
	//int cost[NUM][NUM], num[NUM][NUM] = { { 1, 1, 9, 1, 1, 3 }, { 3, 1, 9, 7, 1, 4 }, { 4, 1, 9, 1, 1, 2 }, { 5, 1, 1, 1, 5, 2 }, { 6, 1, 9, 3, 1, 3 }, { 3, 1, 4, 2, 1, 2 } };
	int cost[NUM][NUM], num[NUM][NUM];
	int min_value = INT_MAX;
	solution aa;
	pair>>re,minimun;//first部分表示代价综合,后部分表示该代价下的路径
	for (int i = 0; i < NUM; i++){
		re.first = 0;
		re.second.clear();
		for (int i = 0; i < NUM; i++){
			for (int j = 0; j < NUM; j++){
				cost[i][j] = INT_MAX;
				do{
					num[i][j] = rand() % 20;
				} while (num[i][j] == 0);
			}
		}
		re = aa.The_pipeline(num,cost, i, 0);
		for (int j = 0; j < (int)re.second.size() / 2; j++){
			pairtmp;
			tmp = re.second[j];
			re.second[j] = re.second[re.second.size() - j - 1];
			re.second[re.second.size() - j - 1] = tmp;
		}
		if (re.first < min_value){
			min_value = re.first;
			minimun = re;
		}
	}
	cout << "Thie minimun cost is :" << min_value << endl;
	return 0;
}

该问题的递归方程为:

min[i][j]=min{min[i-1][j],min[i+1][j],min[i][j-1]}+num[i][j];

其中min[i][j]表示截止挖到[i,j]的最小代价值,num[i][j]表示需要在[i,j]挖通管道的代价.

如有问题,email联系.