线性回归算法实现(最小二乘法, 梯度下降)
一、最小二乘法
import numpy as np;
import matplotlib.pyplot as plt;初始化数据,网上随便找的数据, 说是奥运会100米短跑用时,以及对应的年份。
dataArray = np.array([[12, 1896], [11, 1900], [11, 1904], [10.8, 1908], [10.8, 1912],
[10.8, 1920], [10.6, 1924], [10.8, 1928], [10.3, 1932], [10.3, 1936],
[10.3, 1948], [10.5, 1956], [10.2, 1960], [10.0, 1964], [9.95, 1968],
[10.14, 1972], [10.06, 1976], [10.25, 1980], [9.99, 1984], [9.92, 1988],
[9.96, 1992], [9.84, 1996], [9.87, 2000], [9.85, 2004], [9.96, 2008]]);显示一下数据,看是什么样的。
plt.scatter(dataArray[:, 1], dataArray[:, 0])
plt.show()rows = dataArray.shape[0]
Y = np.matrix(dataArray[:, 0:1])
X = np.ones((rows, 2))
X[:, 1] = dataArray[:, 1]
X = np.matrix(X)使用最小二乘法公式进行计算, 得到直线的参数W, 显示出直线和数据点。最小二乘法的原理涉及到投影矩阵和最大似然定理等。
W = (X.T*X).I*X.T*Y
x = np.arange(1896, 2012, 1)
y = W[0, 0] + W[1, 0]*x
plt.scatter(dataArray[:, 1], dataArray[:, 0])
plt.plot(x, y)
plt.show()二、梯度下降法
对数据进行初始化,和预处理。不进行预处理优化时比较费时,很难达到最优点。
Y = dataArray[:, 0:1]
X = dataArray[:, 1:2]
X = (X - 1950) / 50;
Y = Y - 10.5a0 = np.random.randn();
a1 = np.random.randn();
x = np.arange(-1, 1.2, 0.05)
y = a0 + a1*x
plt.scatter(X, Y)
plt.plot(x, y)
plt.show()使用梯度下降法进行优化,并显示图像。
a0new = a0;
a1new = a1;
stepSize = 0.0003;
for i in range(20000):
a0new = a0 - stepSize/rows * sum(a0 + a1*X - Y)
a1new = a1 - stepSize/rows * sum((a0 + a1*X - Y)*X)
a0 = a0new;
a1 = a1new;
if(i % 2000 == 0):
print("i:", i);
print("a0", a0);
print("a1", a1);
x = np.arange(-1, 1.2, 0.05)
y = a0 + a1*x
predY = a0 + a1*X
loss = sum(pow((Y - predY), 2))/rows;
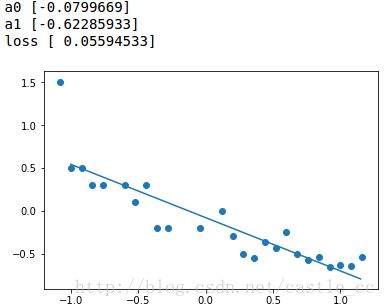
print("loss", loss)
plt.scatter(X, Y)
plt.plot(x, y)
plt.show()直线逐渐的拟合了数据点。与最小二乘法的图像基本一致。
完整代码地址:Linear_Regression