图像频域滤波处理

1.图像频域滤波的基本概念
空间域和频域滤波的基础都是卷积定理。该定理可以写为

和
其中，符号*表示两个函数的卷积，双箭头两边的表达式组成了傅里叶变换对。第一个表达式表明两个空间函数的卷积可以通过计算两个傅里叶变换函数的乘积逆变换得到。在滤波问题上，我们更关注第一个表达式，它构成了整个频域滤波的基础，式中的乘积实际上就是两个二维矩阵F(u,v)和H(u,v)对应元素之间的乘积。
傅立叶变换相关函数
MATLAB提供了几个和傅里叶变换相关的函数。其说明如下：
fft2(F); 二维傅立叶变换
abs(F); 获得傅立叶频谱
fftshift(F); 将变换的原点移至频率矩形的中心
ifft2(F); 二维傅立叶反变换
real(ifft2(F)); 提取变换后的实部
imag(ifft2(F)); 提取变换后的虚部
2. 频域滤波的基本步骤
频域滤波通常应遵循以下步骤。
（1）计算原始图像f(x,y)的DFT，得到F(u,v)。
（2）将频谱F(u,v)的零频点移动到频谱图的中心位置。
（3）计算滤波器函数H(u,v)与F(u,v)的乘积G(u,v)。
（4）将频谱G(u,v)的零频点移回到频谱图的左上角位置。
（5）计算第（4）步计算结果的傅里叶反变换g(x,y)。
（6）取g(x,y)的实部作为最终滤波后的结果图像。
按照该步骤，在MATLAB中很容易编程实现频域滤波。滤波能否取得理想结果的关键取决于频域滤波函数H（u，v），常常称之为滤波器，或滤波器传递函数。因为它在滤波中抑制或滤除了频谱中某些频率的分量，而保留其他一些频率不受影响。

3 频域滤波器
1 理想低通滤波器(ILPF)

D(u,v)是点(u,v)距频率原点的距离，D0为截止频率。如果图像大小为M×N，其变换亦为M×N。中心化之后，矩形中心在（M/2，N/2）

则

说明：在半径为D0的圆内，所有频率没有衰减地通过滤波器，而在此半径的圆之外的所有频率完全被衰减掉。虽然这个滤波器不能使电子元件来模拟实现，但可以在计算机中用传递函数实现。由于理想低通滤波器的过度特性过于急峻，所以会产生了振铃现象。

2 n阶巴特沃斯低通滤波器(BLPF)

n表示的是巴特沃斯滤波器的次数。随着次数的增加，振铃现象会越来越明显。与理想低通滤波器不同的是，巴特沃斯低通滤波器传递函数并不是在D0处突然不连续。对于具有平滑传递函数的滤波器，我们通常要定义一个截止频率，在该点处H(u,v)会降低为其最大值的某个给定比例。例如当D(u,v)=D0时，H(u,v)=0.5。通常，BLPF的平滑效果好于ILPF。

3 高斯低通滤波器（GLPF）

D0为截止频率，当D(u,v)=D0 时，滤波器下降到其最大值的0.607，无振铃现象。

4 理想高通滤波器(IHPF)

D(u,v)是点(u,v)距频率原点的距离，D0为截止频率。如果图像大小为M×N，其变换亦为M×N。中心化之后，矩形中心在（M/2，N/2）
则

在半径为D0的圆外，所有频率没有衰减地通过滤波器，而在此半径的圆之内的所有频率完全被衰减掉。虽然这个滤波器不能使电子元件来模拟实现，但可以在计算机中用传递函数实现。由于理想高通滤波器的过度特性过于急峻，所以会产生了振铃现象。
![理想高通滤波器三维透视图](https://img-blog.csdn.net/20150423211457107)
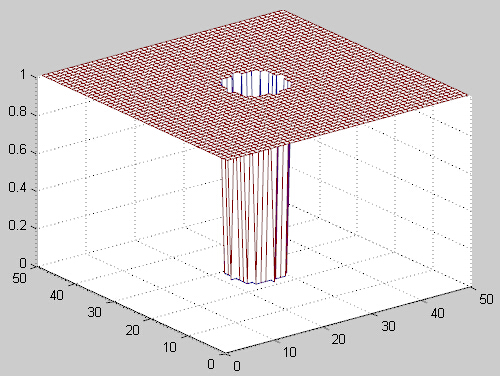
5  n阶巴特沃斯高通滤波器(BHPF)

n表示的是巴特沃斯滤波器的次数。随着次数的增加，振铃现象会越来越明显。与理想高通滤波器不同的是，巴特沃斯高通滤波器传递函数并不是在D0处突然不连续。对于具有平滑传递函数的滤波器，我们通常要定义一个截止频率，在该点处H(u,v)会降低为其最大值的某个给定比例。例如当D(u,v)=D0时，H(u,v)=0.5。通常，BHPF的平滑效果好于IHPF。

6 高斯高通滤波器（GHPF）

程序代码如下：

function [U,V] = dftuv( M,N )
%DFTUV computes meshgrid frequency matrices
%set up range of variables
u=0:(M-1);
v=0:(N-1);
%compute the indices for use in meshgrid
idx=find(u > M/2);
u(idx)=u(idx)-M;
idy=find(v > N/2);
v(idy)=v(idy)-N;
%compute the meshgrid arrays
[V,U]=meshgrid(v,u);
End

function [H,D] = lpfilter( type,M,N,D0,n)
%lpfilter computes frequency domin lowpass filters
%H creates the transfer function of a lowpass filter

%use function dftuv to set up the meshgrid arrays needed for computing 
%the required distances
[U,V]=dftuv(M,N);
D=sqrt(U.^2+V.^2);
%begin filter computations
switch type
    case 'ideal'
        H=double(D<=D0);
    case 'btw'
        if nargin ==4
            n=1;
        end
        H=1./(1+(D./D0).^(2*n));
    case 'gaussian'
        H=exp(-(D.^2)./(2*(D0^2)));
    otherwise
        error('unknown filter type')  
end        
end

function H = hpfilter( type,M,N,D0,n )
%hpfilter computes frequency domin highpass filters
%H creates the transfer function of a highpass filter
%the transfer function Hhp of a highpass filter is 1-Hlp
%we can use function lpfilter to generate highpass filters.
if nargin==4
    n=1; 
end
%generate highpass filter.
hlp=lpfilter(type,M,N,D0,n);
H=1-hlp;

end

%图像频域高通滤波主程序
clear all;
I=imread('man.bmp'); %读入原图像
F=fft2(double(I));   %快速傅里叶变换
F=fftshift(F);       %图像零频点移动到频谱图中心

[M,N]=size(F);       %计算矩阵F的大小
%调用高通滤波器函数
H=hpfilter('ideal',M,N,40); 
%H=hpfilter('btw',M,N,40);
%H=hpfilter('gaussian',M,N,40);

H=fftshift(H);
G =F .* H;        %应用滤镜
%傅里叶反变换
g=ifft2(G);
%显示并比较结果
figure(1),imshow(I);  
title('显示原图像');
figure(2),imshow(log(1+abs(F)),[]);  
title('傅立叶变换后的频谱图');
figure(3),imshow(H,[]);
title('高通滤波器频域图像');
figure(4),imshow(log(1+abs(G)),[]);
title('高通滤波器处理后的频谱图');
figure(5),imshow(abs(real(g)),[]);
title('傅里叶反变换后的图像');

结论
在频谱中，低频主要对应图像在平滑区域的总体灰度级分布，而高频对应图像的细节部分，如边缘和噪声。