NLP实践六：词袋模型到word2vec

一.词袋模型

来自词袋模型bow和词向量模型word2vec
所谓词袋模型BOW，就是将文本/Query看作是一系列词的集合。由于词很多，所以咱们就用袋子把它们装起来，简称词袋。
举个例子：文本1：苏宁易购/是/国内/著名/的/B2C/电商/之一
这是一个短文本。“/”作为词与词之间的分割。从中我们可以看到这个文本包含“苏宁易购”，“B2C”，“电商”等词。换句话说，该文本的的词袋由“苏宁易购”，“电商”等词构成。就像这样：

那在计算机中怎么表示词袋模型呢？其实很简单，给每个词一个位置/索引就可以了。例如，我们令“苏宁易购”的索引为0，“电商”的索引为1，其他以此类推。则该文本的词袋就变成了：

词袋变成了一串数字的（索引）的集合。】
实际应用中，考虑用更简单的数据结构来组织词袋模型。既然刚才说词是用数字（索引）来表示的，那自然会想到数组。例如
Intwords[10000] = {1,20,500,0,……}
索引:{0,1,2,3,……}
词: {苏宁易购,是,国内,B2C,……}
数组的下标表示不同的词，数组中的元素表示词的权重（如：TF，TF-IDF）。更为一般的，词的索引可以用词的HashCode来计算，即：Index(苏宁易购) = HashCode(苏宁易购)。将词散列到数组的某个位置，并且是固定的（理论上会有冲突，需要考虑冲突的问题）。因此，HashCode这个函数起到了字典的作用。转化成了数组，接下来计算余弦相似度啥的就好办多了。这就是词袋模型。

二 wordembedding

Word embedding 是NLP中一组语言模型（language modeling）和特征学习技术（feature learning techniques）的总称，这些技术会把词汇表中的单词或者短语（words or phrases）映射成由实数构成的向量上。
参考Word Embedding与Word2Vec
Word Embedding&word2vec

one-hot

最简单的一种Word Embedding方法，就是基于词袋（BOW）的One-Hot表示。这种方法，把词汇表中的词排成一列，对于某个单词 A，如果它出现在上述词汇序列中的位置为 k，那么它的向量表示就是“第 k 位为1，其他位置都为0 ”的一个向量。

     例如，有语料库如下：

John likes to watch movies. Mary likes movies too.

John also likes to watch football games.

把上述语料中的词汇表整理出来并排序（具体的排序原则可以有很多，例如可以根据字母表顺序，也可以根据出现在语料库中的先后顺序）

假设我们的词汇表排序结果如下：

{“John”: 1, “likes”: 2, “to”: 3, “watch”: 4, “movies”: 5, “also”:6, “football”: 7, “games”: 8, “Mary”: 9, “too”: 10}

那么则有如下word的向量表示：
John: [1, 0, 0, 0, 0, 0, 0, 0, 0, 0]
likes: [0, 1, 0, 0, 0, 0, 0, 0, 0, 0]
……
此时，你也可以进一步地把文档也表示成向量。方法就是直接将各词的词向量表示加和，于是则有原来的两句话的向量表示如下：
John likes to watch movies. Mary likes movies too.=[1, 2, 1, 1, 2, 0, 0, 0, 1, 1]
John also likes to watch football games.=[1, 1, 1, 1, 0, 1, 1, 1, 0, 0]
One-hot方法很简单，但是它的问题也很明显：
1）它没有考虑单词之间相对位置的关系；
2）词向量可能非常非常长！

共现矩阵Cocurrence matrix

共现矩阵Cocurrence matrix：一定程度上解决没有考虑单词之间相对位置的关系的问题。
实现方法：某个词的意思跟它临近的单词是紧密相关的。可以设定一个窗口（大小一般是5~10)，利用这种共现关系生成词向量（得到一个对称矩阵——共现矩阵，该矩阵统计当前词与其他词在同一窗口中的次数，如果词数是n，那么矩阵是nXn）。
例如，现在我们的语料库包括下面三份文档资料：

I like deep learning.

I like NLP.

I enjoy flying.

作为示例，我们设定的窗口大小为1，也就是只看某个单词周围紧邻着的那个单词。此时，将得到一个对称矩阵——共现矩阵。因为在我们的语料库中，I 和 like做为邻居同时出现在窗口中的次数是2，所以下表中I 和like相交的位置其值就是2。这样我们也实现了将word变成向量的设想，在共现矩阵每一行（或每一列）都是对应单词的一个向量表示。

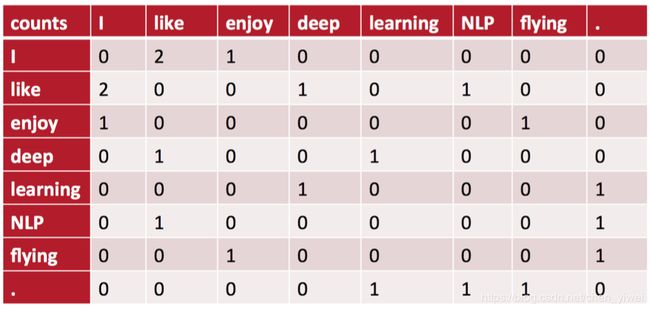
缺点：仍然面对维度灾难。这SVD或者PCA等一些常用的降维方法也会带来其他的一些问题，例如，我们的词汇表中有新词加入，很难为他分配一个新的向量。

Distributed representation

Distributed representation可以解决One hot representation的问题，它的思路是通过训练，将每个词都映射到一个较短的词向量上来。所有的这些词向量就构成了向量空间，进而可以用普通的统计学的方法来研究词与词之间的关系。这个较短的词向量维度是多大呢？这个一般需要我们在训练时自己来指定。
　比如下图我们将词汇表里的词用"性别",“高贵”, "年龄"和"食物"等多个维度来表示，King这个词对应的词向量可能是(-0.95,0.93,0.7,0.02 …)。当然在实际情况中，我们并不能对词向量的每个维度做一个很好的解释。

有了用Distributed Representation表示的较短的词向量，我们就可以较容易的分析词之间的关系了，比如我们将词的维度降维到2维，有一个有趣的研究表明，用下图的词向量表示我们的词时，我们可以发现：
$$King-Man+Woman=Queen$$

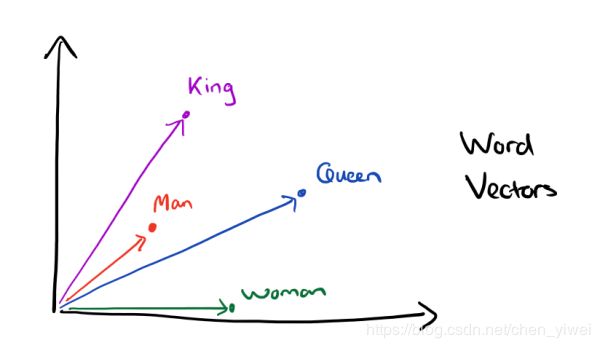
word2vec

“word2vec” 是指将词语word 变成向量vector 的过程，这一过程通常通过浅层的神经网络完成，例如CBOW或者skip gram，这一过程同样可以视为构建词嵌表E的过程”
两个算法：

Skip-grams (SG)：预测上下文

Continuous Bag of Words (CBOW)：预测目标单词

两种稍微高效一些的训练方法：

Hierarchical softmax

Negative sampling

三 word2vec 的训练

参考基于Negative Sampling的模型
word2vec原理推导与代码分析
NLP之——Word2Vec详解
Word Embedding&word2vec

两种算法

CBOW

CBOW是已知上下文，估算当前词语的语言模型.从数学上看，CBoW模型等价于一个词袋模型的向量乘以一个Embedding矩阵，从而得到一个连续的embedding向量。这也是CBoW模型名称的由来.

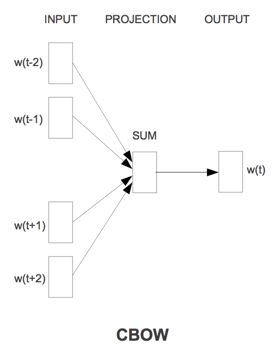
其学习目标是最大化对数似然函数：
$$$$

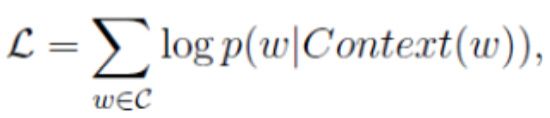
其中，w表示语料库C中任意一个词。从上图可以看出，对于CBOW，输入层是上下文的词语的词向量（什么！我们不是在训练词向量吗？不不不，我们是在训练CBOW模型，词向量只是个副产品，确切来说，是CBOW模型的一个参数。训练开始的时候，词向量是个随机值，随着训练的进行不断被更新）。
投影层对其求和，所谓求和，就是简单的向量加法。

输出层输出最可能的w。由于语料库中词汇量是固定的|C|个，所以上述过程其实可以看做一个多分类问题。给定特征，从|C|个分类中挑一个。
比如下面这段话，我们的上下文大小取值为4，特定的这个词是"Learning"，也就是我们需要的输出词向量,上下文对应的词有8个，前后各4个，这8个词是我们模型的输入。由于CBOW使用的是词袋模型，因此这8个词都是平等的，也就是不考虑他们和我们关注的词之间的距离大小，只要在我们上下文之内即可。

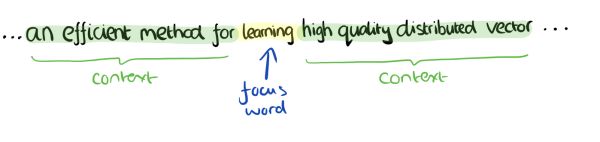
这样样我们这个CBOW的例子里，我们的输入是8个词向量，输出是所有词的softmax概率（训练的目标是期望训练样本特定词对应的softmax概率最大），对应的CBOW神经网络模型输入层有8个神经元，输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法，我们可以求出DNN模型的参数，同时得到所有的词对应的词向量。这样当我们有新的需求，要求出某8个词对应的最可能的输出中心词时，我们可以通过一次DNN前向传播算法并通过softmax激活函数找到概率最大的词对应的神经元即可。

Skip-gram

Skip-gram逆转了CBOW的因果关系而已，即已知当前词语，预测上下文 。

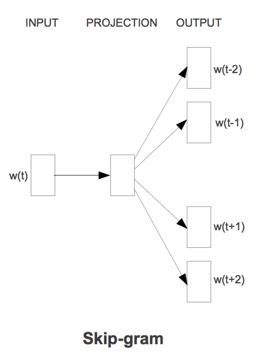
将Skip-gram模型的前向计算过程写成数学形式，我们得到：
$$p(w_o|w_i)=\frac{e^{U_o\cdot V_i}}{{\sum }_j{e}^{U_j\cdot V_i}}$$
其中，$V_i$是Embedding层矩阵里的列向量，也被称为$w_i$的input vector。$U_j$是softmax层矩阵里的行向量，也被称为$w_i$的output vector.
Skip-gram模型的本质是计算输入word的input vector与目标word的output vector之间的余弦相似度，并进行softmax归一化
还是上面的例子，我们的上下文大小取值为4， 特定的这个词"Learning"是我们的输入，而这8个上下文词是我们的输出。这样我们这个Skip-Gram的例子里，我们的输入是特定词， 输出是softmax概率排前8的8个词，对应的Skip-Gram神经网络模型输入层有1个神经元，输出层有词汇表大小个神经元。隐藏层的神经元个数我们可以自己指定。通过DNN的反向传播算法，我们可以求出DNN模型的参数，同时得到所有的词对应的词向量。这样当我们有新的需求，要求出某1个词对应的最可能的8个上下文词时，我们可以通过一次DNN前向传播算法得到概率大小排前8的softmax概率对应的神经元所对应的词即可。

加速训练方法

Hierarchical Softmax

定义：Hierarchical Softmax是一种对输出层进行优化的策略，输出层从原始模型的利用softmax计算概率值改为了利用Huffman树计算概率值。它的基本思想是将复杂的归一化概率分解为一系列条件概率乘积的形式
$$p(v|context)=\prod _{i=1}^{m}p(b_i(v)|b_1(v),...,b_{i-1}(v),context)$$

其中，每一层条件概率对应一个二分类问题，可以通过一个简单的逻辑回归函数去拟合。这样，我们将对V个词的概率归一化问题，转化成了对logV个词的概率拟合问题。

我们可以通过构造一颗分类二叉树来直观地理解这个过程。首先，我们将原始字典D划分为两个子集D1、D2，并假设在给定context下，target word属于子集D1的概率$p(w_t\in D_1|context)$服从logistical function的形式：
$$p(w_t\in D_1|context)=\frac{1}{1+e^{-U_{D_{root}}\cdot V_{w_t}}}$$

其中，$U_{D_{root}}$和$V_{w_t}$都是模型的参数。

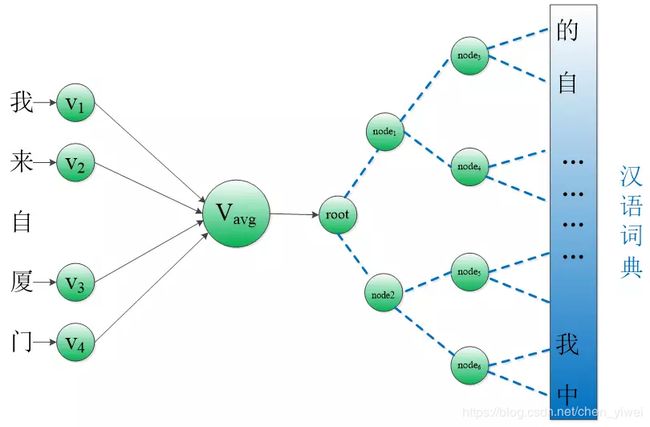
接下来，我们可以对子集D1和D2进一步划分。重复这一过程，直到集合里只剩下一个word。这样，我们就将原始大小为V的字典D转换成了一颗深度为logV的二叉树。树的叶子节点与原始字典里的word一一对应；非叶节点则对应着某一类word的集合。显然，从根节点出发到任意一个叶子节点都只有一条唯一路径——这条路径也编码了这个叶子节点所属的类别。

同时，从根节点出发到叶子节点也是一个随机游走的过程。因此，我们可以基于这颗二叉树对叶子节点出现的似然概率进行计算。例如，对于训练样本里的一个target $word{w}_t$，假设其对应的二叉树编码为$\{1,0,1,...,1\}$，则我们构造的似然函数为：
$$p(w_t|context)=p(D_1=1|context)p(D_2=0|D_1=1)\dots p(w_t|D_k=1)$$

乘积中的每一项都是一个逻辑回归的函数。

我们可以通过最大化这个似然函数来求解二叉树上的参数——非叶节点上的向量，用来计算游走到某一个子节点的概率。
层次Softmax是一个很巧妙的模型。它通过构造一颗二叉树，将目标概率的计算复杂度从最初的V降低到了logV 的量级。不过付出的代价是人为增强了词与词之间的耦合性。例如，一个word出现的条件概率的变化，会影响到其路径上所有非叶节点的概率变化，间接地对其他word出现的条件概率带来不同程度的影响。因此，构造一颗有意义的二叉树就显得十分重要。实践证明，在实际的应用中，基于Huffman编码的二叉树可以满足大部分应用场景的需求。

Negative Sampling

比如我们有一个训练样本，中心词是w,它周围上下文共有$2c$个词，记为$context(w)$。由于这个中心词w,的确和context(w)相关存在，因此它是一个真实的正例。通过Negative Sampling采样，我们得到neg个和w不同的中心词$w_i,i=1,2,..neg$，这样$context(w)$和$w_i$就组成了neg个并不真实存在的负例。利用这一个正例和neg个负例，我们进行二元逻辑回归，得到负采样对应每个词$w_i$对应的模型参数${\theta }_i$，和每个词的词向量。
当我们用训练样本 ( input word: “fox”，output word: “quick”) 来训练我们的神经网络时，“ fox”和“quick”都是经过one-hot编码的。如果我们的vocabulary大小为10000时，在输出层，我们期望对应“quick”单词的那个神经元结点输出1，其余9999个都应该输出0。在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们称为“negative” word。
当使用负采样时，我们将随机选择一小部分的negative words（比如选5个negative words）来更新对应的权重。我们也会对我们的“positive” word进行权重更新（在我们上面的例子中，这个单词指的是”quick“）
隐层-输出层拥有300 x 10000的权重矩阵。如果使用了负采样的方法我们仅仅去更新我们的positive word-“quick”的和我们选择的其他5个negative words的结点对应的权重，共计6个输出神经元，相当于每次只更新 300 x 6 = 1800 个权重。对于3百万的权重来说，相当于只计算了0.06%的权重，这样计算效率就大幅度提高
使用“一元模型分布（unigram distribution）”来选择“negative words”。

一个单词被选作negative sample的概率跟它出现的频次有关，出现频次越高的单词越容易被选作negative words。

代码中的公式实现如下: