傅立叶变换、Gabor变换与小波变换

傅立叶变换

数字图像处理的方法主要分成两种：空域分析法和频域分析法。空域分析法就是对图像矩阵进行处理；频域分析法是通过图像变换将图像从空域变换到频域，从另外一个角度来分析图像的特征并进行处理。频域分析法在图像增强、图像复原、图像编码压缩及特征编码压缩方面有着广泛应用。

如果一个信号 f(t) f ( t ) 在 (−∞,+∞) ( − ∞ , + ∞ ) 上满足：

1. f(t) f ( t ) 在任一有限区间上满足狄氏条件；
   在一个函数周期内，间断点的数目是有限的，极大值和极小值的数目是有限的，来保证最终条件：信号 f(t) f ( t ) 绝对可积
2. f(t) f ( t ) 在 (−∞,+∞) ( − ∞ , + ∞ ) 上绝对可积即 ∫+∞−∞(|f(t)|)dt<∞ ∫ − ∞ + ∞ ( | f ( t ) | ) d t < ∞

就可以通过傅里叶变换把时域信号 f(t) f ( t ) 转化到频域进行处理，傅立叶变换函数如下：

F(ω)=∫+∞−∞f(t)e−jωtdt=F[f(t)] F ( ω ) = ∫ − ∞ + ∞ f ( t ) e − j ω t d t = F [ f ( t ) ]

然后再通过傅里叶反变换把频域信号转化到时域，傅立叶逆变换：

f(t)=12π∫+∞−∞F(ω)ejωtdω=F−1[f(t)] f ( t ) = 1 2 π ∫ − ∞ + ∞ F ( ω ) e j ω t d ω = F − 1 [ f ( t ) ]

傅里叶变换是线性系统分析的有力工具，提供了一种把时域信号转换到频域进行分析的途径，时域和频域之间是一对一的映射关系。图像的频率是表征图像中灰度变化剧烈程度的指标，是灰度在平面空间上的梯度。如：大面积的沙漠在图像中是一片灰度变化缓慢的区域，对应的频率值很低；而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域，对应的频率值较高。

傅立叶变换的不足

经典Fourier变换只能反映信号的整体特性（时域，频域）。对傅里叶谱中的某一频率，无法知道这个频率是在什么时候产生的。从傅里叶变换的定义也可看出，傅里叶变换是信号在整个时域内的积分，因此反映的是信号频率的统计特性，没有局部化分析信号的功能。另外，要求信号满足平稳条件。傅里叶变换时域和频域是完全分割开来的。

由 F(ω)=∫+∞−∞f(x)e−jωxdx F ( ω ) = ∫ − ∞ + ∞ f ( x ) e − j ω x d x 可知，要用Fourier变换研究时域信号频谱特性，必须要获得时域中的全部信息，

信号在某时刻的一个小的邻域内发生变化，那么信号的整个频谱都要受到影响，而频谱的变化从根本上来说无法标定发生变化的时间位置和发生变化的剧烈程度。也就是说，Fourier变换对信号的齐性不敏感。Fourier变换不能给出在各个局部时间范围内部频谱上的谱信息描述。然而在实际应用中齐性正是我们所关心的信号局部范围内的特性。如，音乐，语言信号等。即：局部化时间分析，图形边缘检测，地震勘探反射波的位置等信息极重要。

因此，为了解决傅里叶变换的局限性，产生了Gabor变换和小波变换。

Gabor变换

Gabor变换是D.Gabor 1946年提出的，为了由信号的Fourier变换提取局部信息，引入了时间局部化的窗函数，得到了窗口Fourier变换。由于窗口Fourier变换只依赖于部分时间的信号，所以，现在窗口Fourier变换又称为短时Fourier变换，这个变换又称为Gabor变换。

Gabor变换相比于Fourier变换来说是积分时间上的改变，Fourier变换是基于整个时间域 (−∞,+∞) ( − ∞ , + ∞ ) 上的积分，而Gabor变换是基于一个局部时间窗口上的积分。

Gabor的优点

Gabor小波与人类视觉系统中简单细胞的视觉刺激响应非常相似。在提取目标的局部空间和频率域信息方面具有良好的特性。Gabor小波对于图像的边缘敏感，能够提供良好的方向选择和尺度选择特性，而且对于光照变化不敏感，能够很好的适应光照的变换。上述特点使得Gabor小波被广泛用于视觉信息理解和图像处理领域。

传统的傅立叶变换相比，Gabor小波变换具有良好的时频局部化特性。即非常容易地调整Gabor滤波器的方向、基频带宽及中心频率从而能够最好的兼顾信号在时空域和频域中的分辨能力；Gabor小波变换具有多分辨率特性即变焦能力。即采用多通道滤波技术，将一组具有不同时频域特性的Gabor小波应用于图像变换，每个通道都能够得到输入图像的某种局部特性，这样可以根据需要在不同粗细粒度上分析图像。此外，在特征提取方面，Gabor小波变换与其它方法相比：一方面其处理的数据量较少，能满足系统的实时性要求；另一方面，小波变换对光照变化不敏感，且能容忍一定程度的图像旋转和变形，当采用基于欧氏距离进行识别时，特征模式与待测特征不需要严格的对应，故能提高系统的，能满足系统的实时性要求；另一方面，小波变换对光照变化不敏感，且能容忍一定程度的图像旋转和变形，当采用基于欧氏距离进行识别时，特征模式与待测特征不需要严格的对应，故能提高系统的鲁棒性

Gabor滤波器和脊椎动物视觉皮层感受野响应的比较：第一行代表脊椎动物的视觉皮层感受野，第二行是Gabor滤波器，第三行是两者的残差。可见两者相差极小。Gabor滤波器的这一性质，使得其在视觉领域中经常被用来作图像的预处理。

Gabor定义

1.具体窗函数：Gaussian的Gabor变换定义式

Gabor变换的基本思想是把信号划分成很多小的时间间隔，用傅立叶变换分析每个时间间隔，以便确定信号在该时间间隔存在的频率，其处理方法是对 f(t) f ( t ) 函数加一个滑动窗，在进行傅立叶变换。

设函数 f f 为具体的函数，且 f∈L2(R) f ∈ L 2 ( R ) ，则Gabor变换定义为：

Gf(a,b,ω)=∫+∞−∞f(t)ga(t−b)e−iωtdt G f ( a , b , ω ) = ∫ − ∞ + ∞ f ( t ) g a ( t − b ) e − i ω t d t

其中， ga(t)=12πa√exp(−t24a) g a ( t ) = 1 2 π a e x p ( − t 2 4 a ) 是高斯函数，称为窗函数，其中 a>0 a > 0 ， b>0 b > 0 。 ga(t−b) g a ( t − b ) 是一个时间局部化的窗函数，其中参数 b b 用于平行移动窗口，以便于覆盖整个时域，对参数 b b 积分，则有 ∫+∞−∞Gf(a,b,ω)db=f^(ω) ∫ − ∞ + ∞ G f ( a , b , ω ) d b = f ^ ( ω ) , ω∈R ω ∈ R

信号的重构表达式为： f(t)=12π∫+∞−∞∫+∞−∞Gf(a,b,ω)ga(t−b)eiωtdωdb f ( t ) = 1 2 π ∫ − ∞ + ∞ ∫ − ∞ + ∞ G f ( a , b , ω ) g a ( t − b ) e i ω t d ω d b

Gabor取 g(t) g ( t ) 函数为高斯函数有两个原因：

一是高斯函数的Fourier变换仍为高斯函数，这使得Fourier逆变换也是用窗口函数局部化，同时体现了频域的局部化；

二是Gabor变换是最优的窗口Fourier变换，其意义在于Gabor变换出现之后，采用真正意义上的时间 - 频率分析。

Gabor变换可以达到时频局部化的目的：既能够在整体上提供信号的全部信息，又能提供在任意局部时间内信号变换剧烈程度的信息。简言之，可以同时提供时域和频域局部化的信息。

2.窗口的宽高关系

经理论推导可以得出：高斯窗函数条件下的窗口宽度和高度，其积为一定值。

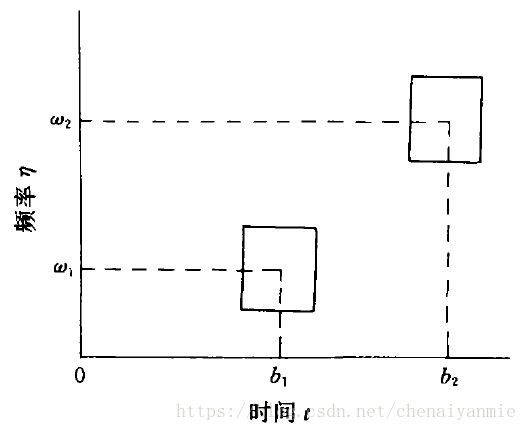
[b−a−−√,b+a−−√]×[ω−1aa√,ω+1aa√]=(2ΔGab,ω)(2ΔHab,ω)=(2Δga)(2Δg1/4a)=2 [ b − a , b + a ] × [ ω − 1 a a , ω + 1 a a ] = ( 2 Δ G b , ω a ) ( 2 Δ H b , ω a ) = ( 2 Δ g a ) ( 2 Δ g 1 / 4 a ) = 2 由此，可以看出 Gabor 变换的局限性：时间频率的宽度对所有频率是固定不变的，实际要求是：窗口的大小应随频率的变化而变化，频率高窗口应越小，这才符合实际问题中的高频信号的分辨率应比低频信号的分辨率要低。

Gabor的不足之处

Gabor变换在一定程度上解决了局部分析的问题，但对于突变信号和非平稳信号仍难以得到满意的结果，即Gabor变换仍存在着较严重的缺陷。
1）Gabor变换的时频窗口大小、形状不变，只有位置变化，而实际应用中常常希望时频窗口的大小、形状要随频率的变化而变化，因为信号的频率与周期成反比，对高频部分希望能给出相对较窄的时间窗口，以提高分辨率，在低频部分则希望能给出相对较宽的时间窗口，以保证信息的完整性，总之是希望能给出能够调节的时频窗；
2）Gabor变换基函数不能成为正交系，因此为了不丢失信息，在信号分析或数值计算时必须采用非正交的冗余基，这就增加了不必要的计算量和存储量。Gabor变换的时间频率窗如下所示：

我们想要的时间-频率窗是这样的：

小波（wavelet）变换

为了解决Gabor变换的局限性，小波变换诞生了。

数学上来说，小波是函数空间 L2(R) L 2 ( R ) 中满足“容许性”条件的一个函数或信号 ψ(x) ψ ( x ) 。对于任意实数对 (a,b) ( a , b ) ，其中参数 a a 必须为非零实数，称如下形式的函数：

Ψa,b(x)=1|a|√ψ(x−ba) Ψ a , b ( x ) = 1 | a | ψ ( x − b a )

为由小波母函数 ψ(x) ψ ( x ) 生成的依赖于参数 (a,b) ( a , b ) 的连续小波函数，简称小波。小波函数在原点附近才有明显偏离水平轴的波动，在远离原点时函数值迅速衰减为零，所以对任意参数 (a,b) ( a , b ) ，小波函数 ψa,b(x) ψ a , b ( x ) 在 x=b x = b 附近存在明显的波动，远离 x=b x = b 的地方迅速衰减到零。小波变换给出了一个可以调节的时频窗口，窗口的宽度随频率变化，频率增高时时间窗口的宽度自动变窄，以提高分辨率，被誉为数学显微镜。

小波变换定义为： Wf(a,b)=1|a|√∫+∞−∞f(t)Ψ(t−ba)dt W f ( a , b ) = 1 | a | ∫ − ∞ + ∞ f ( t ) Ψ ( t − b a ) d t

信号 f(t) f ( t ) 的小波变换是一个二元函数，参数 b b 表示分析的时间中心或时间点，参数 a a 表示的是以 t=b t = b 为中心的波动范围，所以参数 a a 一般称为尺度参数（相当于Gabor变换中的 ω ω ），可以改变频谱结构和窗口的形状，而参数 b b 为时间中心参数（即Gabor变换中的 b b ），所以小波变换也是时频分析函数。

学习小波变换时会发现有许多种类的小波变换，这是因为小波变换与小波母函数 ψ(x) ψ ( x ) 有关，不同的小波母函数 ψ(x) ψ ( x ) 则对应着不同种类的小波变换了，比如Haar小波、Shannon小波、墨西哥草帽状小波等等。可以证明， ψa,b(x) ψ a , b ( x ) 的时频窗口面积与参数 a a 和 b b 无关，仅与 ψ(x) ψ ( x ) 的选取有关，所以不能通过选择参数 a a 和 b b 使时域和频域窗口的半径同时缩小，时域和频域上的分辨率相互牵制，要想使两者的分辨率同时提高，就必须选择适当的小波母函数 ψ(x) ψ ( x ) ，小波母函数趋向于零的速度是衡量小波母函数性质好坏的一个重要标志。

总结分析

傅立叶变换实现了时域到频域的分离转换，适用于确定性信号和平稳信号，属于全局分析，特别适合分析长时间内较稳定的信号；

Gabor变换（窗口傅立叶变换的一种，窗口函数为高斯窗时为Gabor变换）实现了时频分析的局部化，是一种具有单一分辨率（窗函数的大小、形状不变）的时频分析，特别对图像边缘敏感，对光照不敏感；

小波变换具有优良的局部化视频分析特性，可以改变频谱结构和窗口形状（窗口大小是不变的），对分析突变信号和奇异信号非常有效；