离散Gabor变换及代码实现

离散Gabor变换的一般求法

1.首先选取核函数，可根据实际需要选取适当的核函数。如高斯窗函数：

g(t)=(2√T)2e−π(tT)2 g ( t ) = ( 2 T ) 2 e − π ( t T ) 2

则其对偶函数 γ(t)为γ(t)=(12√T)12(K0π)eπ(tT)2∑n+1/2>1/T(−1)ne−π(n+1/2)2 γ ( t ) 为 γ ( t ) = ( 1 2 T ) 1 2 ( K 0 π ) e π ( t T ) 2 ∑ n + 1 / 2 > 1 / T ( − 1 ) n e − π ( n + 1 / 2 ) 2

离散Gabor变换的表达式：

Gmn=∫+∞−∞ϕ(t)g∗(t−mT)e−jnωtdt=∫+∞−∞ϕ(t)g∗mn(t)dt G m n = ∫ − ∞ + ∞ ϕ ( t ) g ∗ ( t − m T ) e − j n ω t d t = ∫ − ∞ + ∞ ϕ ( t ) g m n ∗ ( t ) d t

ϕ(t)=∑∞m=−∞∑∞n=−∞Gmmγ(t−mT)ejnωt=∑∞m=−∞∑∞n=−∞Gmnγ(t) ϕ ( t ) = ∑ m = − ∞ ∞ ∑ n = − ∞ ∞ G m m γ ( t − m T ) e j n ω t = ∑ m = − ∞ ∞ ∑ n = − ∞ ∞ G m n γ ( t )

其中 gmn(t)=g(t−mT)einωt g m n ( t ) = g ( t − m T ) e i n ω t

γ(t) γ ( t ) 是 g(t) g ( t ) 的对偶函数，二者之间有如下双正交关系： ∫∞−∞γ(t)g∗(t−mT)e−jnωtdt=δmδn ∫ − ∞ ∞ γ ( t ) g ∗ ( t − m T ) e − j n ω t d t = δ m δ n

4.Gabor变换的解析理论就是由 g(t) g ( t ) 求对偶函数 γ(t) γ ( t ) 的方法，定义 g(t) g ( t ) 的 Zak 变换为 Zak[g(t)]=g^(t,ω)=∑∞k=−∞g(t−k)e−j2πkω Z a k [ g ( t ) ] = g ^ ( t , ω ) = ∑ k = − ∞ ∞ g ( t − k ) e − j 2 π k ω ，可以证明对偶函数可由下式求出： γ(t)=∫10dωg∗(t,ω) γ ( t ) = ∫ 0 1 d ω g ∗ ( t , ω ) ，有了对偶函数使计算更为简洁方便。

二维Gabor滤波器

二维Gabor变换可以应用到图像分析与压缩中，用Gabor函数形成的二维Gabor滤波器具有在空间域和频率域取得最优局部化的特性，因此能够很好的描述对应于控件频率（尺度）、空间位置及方向选择性的局部结构信息。Gabor滤波器的频率和方向表示接近人类视觉系统对于频率和方向的表示，并且它们常备用于纹理表示和描述。在图像处理领域，Gabor滤波器是一个用于边缘检测的线性滤波器。在空域，一个二维的Gabor滤波器是一个正弦平面波和高斯核函数的乘积。Gabor滤波器是自相似的，也就是说，所有Gabor滤波器都可以从一个母小波经过膨胀和旋转产生。实际应用中，Gabor滤波器可以在频域的不同尺度，不同方向上提取相关特征。

二维Gabor函数如下所示：

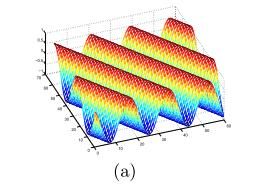
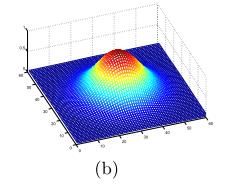
公式中： λ λ 表示正弦函数的波长

ψ ψ 表示正弦函数的相位

σ σ 表示高斯核函数的标准差 ，代表尺度宽度。

θ θ 表示高斯核函数的方向

γ γ 表示x, y 两个方向的高宽比， γ γ 决定了 θ θ 方向， γ=x/y γ = x / y （指定了Gabor函数的椭圆率） ,就是Gabor核的高度height和宽度width的比值

二维Gabor函数的第二种形式如下：

guv(x,y)=k2σ2exp(−k2(x2+y2)2σ2)[exp(ik(xy))−exp(−σ22)] g u v ( x , y ) = k 2 σ 2 e x p ( − k 2 ( x 2 + y 2 ) 2 σ 2 ) [ e x p ( i k ( x y ) ) − e x p ( − σ 2 2 ) ]

其中：

k=(kxky)=(kvcosϕukvsinϕu) k = ( k x k y ) = ( k v c o s ϕ u k v s i n ϕ u )

kv=2−v+22π k v = 2 − v + 2 2 π

ϕu=uπK ϕ u = u π K

guv(x,y)=k2σ2exp(−k2(x2+y2)2σ2)[exp(i(kvcosϕux+kvsinϕuy))−exp(−σ22)] g u v ( x , y ) = k 2 σ 2 e x p ( − k 2 ( x 2 + y 2 ) 2 σ 2 ) [ e x p ( i ( k v c o s ϕ u x + k v s i n ϕ u y ) ) − e x p ( − σ 2 2 ) ]

v v 的取值决定了Gabor滤波的波长， u u 的取值表示 Gabor 核函数的方向， K K 表示总 d d 的方向数，参数 σ/k σ / k 决定了高斯窗口的大小，这里取 σ=2–√π σ = 2 π

二维Gabor函数可以增强边缘以及峰、谷、脊轮廓等底层图像特征，这相当于增强了被认为是面部关键部件的眼睛、鼻子、嘴巴等信息，同时也增强了诸于黑痣、酒窝、伤疤等局部特征，从而使得在保留总体人脸信息的同时增强局部特性成为可能。它的小波特性说明了Gabor滤波结果是描述图像局部灰度分布的有力工具，因此，可以使用Gabor滤波来抽取图像的纹理信息。

然而，大部分基于Gabor特征的人脸识别算法中，只应用了Gabor幅值信息，而没有应用相位信息，主要原因是Gabor相位信息随着空间位置呈周期性变化，而幅值的变化相对平滑而稳定，幅值反映了图像的能量谱，Gabor幅值特征通常称为Gabor 能量特征(Gabor Energy Features）。

Gabor变换代码实现

//构造Gabor函数
    for (int k = 0;k < N;k++)                   //定义N方向
    {
        Theta = PI*((double)k/N);    //0*PI/4,1*PI/4,2*PI/4,3*PI/4
        for (int i = 0;i < gabor_height;i++)    //定义模版大小
        {
            for (int j = 0;j < gabor_width;j++)
            {
                x = j - gabor_width/2;    //-5,-4,-3,-2,-1,0,+1,+2,+3,+4, x轴的坐标和位置
                y = i - gabor_height/2; //-5,-4,-3,-2,-1,0,+1,+2,+3,+4, y轴的坐标和位置

                xtmp = (double)x*cos(Theta) + (double)y*sin(Theta);
                ytmp = (double)y*cos(Theta) - (double)x*sin(Theta);

                tmp1 = /* (1/(2*PI*sigma_x*sigma_y))**/exp(
-(pow(xtmp,2)/pow(sigma_x,2)                             +pow(ytmp,2)/pow(sigma_y,2))/2);
                tmp2 = cos(2*PI*xtmp/Lambda);
                tmp3 = sin(2*PI*xtmp/Lambda);

                re = tmp1*tmp2;
                im = tmp1*tmp3;

                rel[i*gabor_width+j] = re;
                img[i*gabor_width+j] = im;
                //printf("%f,%f\n",re,im);
            }
        }
        //用不同方向的Gabor函数对图像滤波并保存图片 
        g_filer(src_data,src->height,src->width,rel,img,10,10,k);
    }