编译原理（龙书第二版）：语法分析相关习题及总结

一. 考虑以下文法：

S→aTUV∣bV
T→U∣UU
U→ε∣bV
V→ε∣cV

写出每个非终结符号的FIRST集和FOLLOW集

FIRST(S)={a, b} 　FIRST(T)={є, b} 　FIRST(U)={є, b} 　FIRST(V)={є, c}

FOLLOW(S)={$} 　FOLLOW(T)={ b, c, $} 　FOLLOW(U)={ b, c, $} 　FOLLOW(V)={ b, c , $}

FIRST集的求解方法非常简单，因为显而易见，一眼就能看出来。这里就不赘述了。

FOLLOW集的求解就需要细心一点，一不小心就容易漏掉。

求解一个非终结符号的FOLLOW(S),那么就看它出现在产生式右边的地方。

1) 求FOLLOW(S)

因为S是开始符号，$是结束标记，先把$放到FOLLOW(S)中。S没有出现在产生式右边，所以没有了。

2) 求FOLLOW(T)

因为T出现在 s→aTUV 中，所以FIRST(U)中除了 ε 之外的所有符号都在FOLLOW(T)中，也就是把b添加进去。

又因为FIRST(U)中含有 ε ，所以FOLLOW(S)中的所有符号都在FOLLOW(T)中，也就是把$添加进去。

这里很容易忘掉一种情况，那就是U可能为 ε 的情况。这种情况下，FIRST(V)中除了 ε 之外的所有符号都在FOLLOW(T)中，也就是把c添加进去。所以最后得到{ b, c, $} 。

3) 求FOLLOW(U)

因为U出现在 s→aTUV 中，所以FIRST(V)中除了 ε 之外的所有符号都在FOLLOW(U)中，也就是把c添加进去。

又因为U出现在 T→U 中，所以FOLLOW(T)中的所有符号都在FOLLOW(U)中，也就是把b, $添加进去。

4）求FOLLOW(V)

因为U出现在 S→bV 中，所以FOLLOW(S)中的所有符号都在FOLLOW(V)中，也就是把$添加进去。

因为V出现在 U→bV 中，所以FOLLOW(U)中的所有符号都在FOLLOW(V)中，也就是把b, c添加进去。

二. 考虑以下文法：

S→(L)∣a
L→L,S∣S

1. 消除文法的左递归

S→(L)∣a
L→SL′
L→,SL′∣ε

消除左递归的公式如下。

2. 构造文法的LL(1)分析表

3. 对于句子(a, (a, a))，给出语法分析的详细过程

三. 考虑以下文法：

S→aSbS∣bSaS∣ε

这一文法是否是LL(1)文法？给出理由.

答：这一文法不是LL(1)文法。因为S有产生式 S→ε ，但FIRST(S) = {a, b, ε }，FOLLOW(S) = {a, b}，因而FIRST(S)∩FOLLOW(S) ≠ ∅ 。根据LL(1)文法的定义知这一文法不是LL(1)文法。

四. 考虑以下文法：

E→E
E→E+T
E→T
T→TF
T→F
F→F∗
F→a
F→b

1. 写出每个非终端符号的FIRST集和FOLLOW集。

FIRST(E’)= FIRST(E)= FIRST(T)= FIRST(F)={a, b}

FOLLOW(E’)={$} 　 FOLLOW(E)={+, $}　 FOLLOW(T)={+, $, a, b} 　FOLLOW(F)= {+, *, $, a, b}

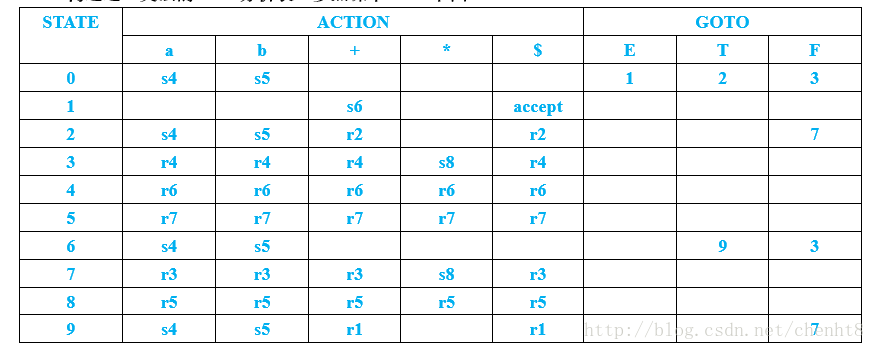
2. 构造识别这一文法所有活前缀（viable prefixes）的LR(0) 自动机

3. 构造这一文法的SLR分析表

4. 给出SLR分析器识别输入串a+ab*的过程

课后练习题4.7.4，4.7.5讲解

4.7.4 说明下面的文法是LALR(1)的，但不是SLR(1)的。

S→Aa∣bAc∣dc∣bda
A→d

LR(0)文法的自动机：

SLR分析表：

从图中可以看出该文法存在移进/规约冲突，例如在状态4，当下一个输入字符为c时，第一个项使得ACTION[4, c] = ”移入8”，而第二个项将ACTION[4, c]设置为”规约A->d”，所以状态4在输入符号c上存在移入/规约冲突，该文法不是SLR(1)。

LR(1)文法的自动机：

LR(1)文法的分析表：

从分析表中可以看出该文法的分析表不存在同心集，没有规约-规约冲突，所以它是LALR(1)的。

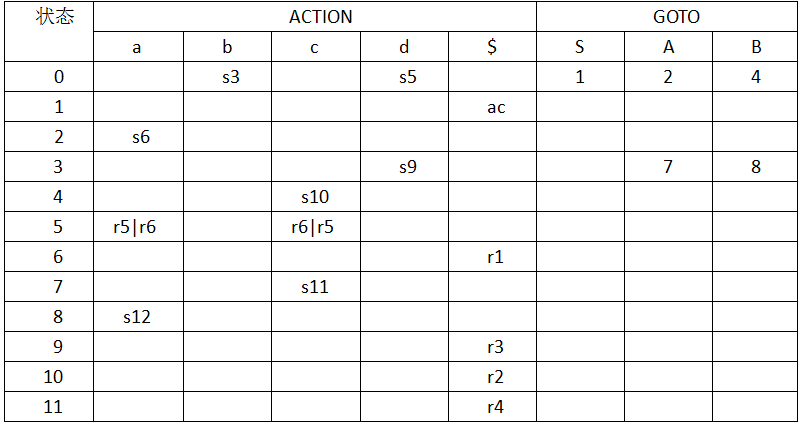
4.7.5 说明下面的文法是LR(1)的，但不是LALR(1)的。

S→Aa∣bAc∣Bc∣bBa
A→d
B→d

LR(1)自动机：

LR(1)分析表：

可以看出分析表并没有冲突，所以该文法是LR(1)的。同时观察分析表可发现，状态5和9存在同心集，可以合并为项集A->d, a/c B->d, a/c 。

合并项集之后就存在了规约/规约冲突。当输入符号为a时，第一个项设置ACTION[5, a]为“规约A->d”，而第二个项设置ACTION[5, a]为“规约B->d”。当输入符号为c时也同理。所以该文法不是LALR(1)的。

几种文法的判断方法总结

1. LL(1)文法

一个文法G是LL(1)的，当且仅当G的任意两个不同的产生式A-> a | b满足以下两个条件：

• FIRST(a)与FIRST(b)的交集为 ∅
• 若 ε 在FIRST(a)中，且FOLLOW(A)与FIRST(b)的交集为 ∅ 。
  注意：第二个条件a和b的位置可互换，也就是说只要a、b中有一个的FIRST集中含有 ε ，那就看另一个。

2. LR(1)文法

LR(1)是在LR(0)自动机的基础上加入了向前搜索符号，如果存在移入-规约冲突，我们就说这个文法不是LR(1)的。如果不存在就是LR(1)文法。

3. SLR(1)文法

SLR(1)文法的自动机、文法分析表全都是LR(0)的，只要找到一个冲突，就不是SLR(1)文法。如果什么冲突也找不到，那就是SLR(1)文法了。

4. LALR(1)文法

LALR(1)文法是在LR(1)的基础上寻找同心集，如果存在同心集，那么就可以合并同心集，也就是存在规约-规约冲突，所以就不是LALR(1)文法。如果找不到同心集，就是LALR(1)文法。

注意：合并同心集，只会产生规约-规约冲突。