List-wise Ranking

背景

ranking is a prediction task on list of objects. 所以 point-wise, pair-wise 等方法的训练任务与工作场景有差异, list-wise 理应更好.

list-wise ranking with S-IE

该论文见参考[1].

Session Infomation Embedding (S-IE)

算是一个预训练, task为正负样本二分类, 为后面list-wise作准备.

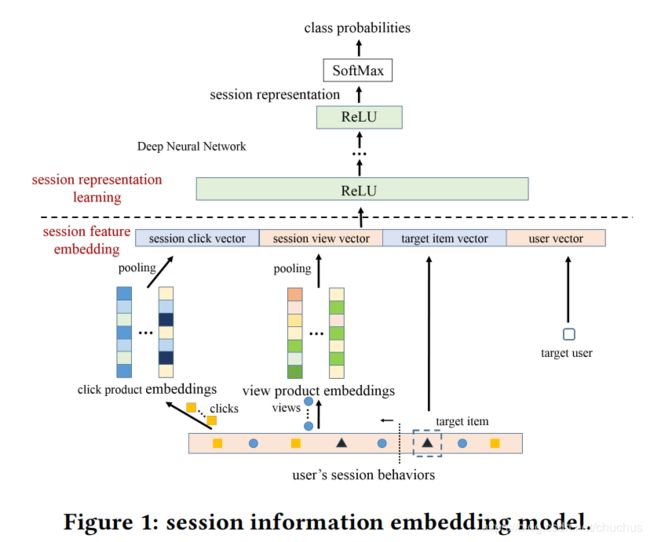
图: 将点击与曝光内容分别pooling, 后与 target,user 作concat.

list-wise ranking

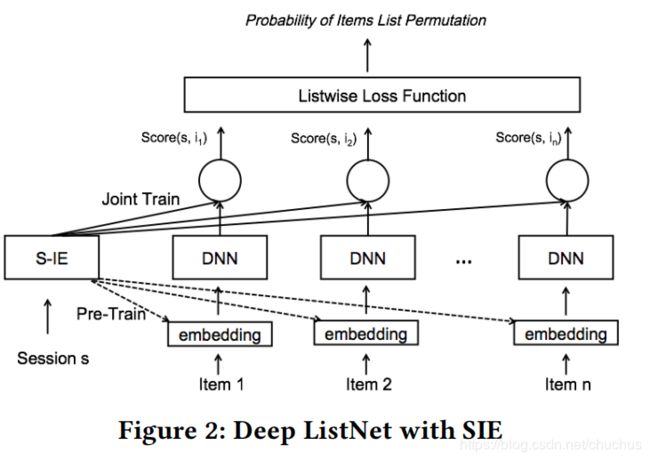
图 公式书写太差, 有误, (1)式中分子下标i可能为$t$,分母下标i可能为$l$; (2)式中i及右括号应放在上标位置.

实验

• 数据集. CIKM CUP 2016.是电商网站搜索引擎的日志.
• ndcg作指标. ctr预估, 通常用二分类的任务去做, 其指标为AUC/GAUC. 现在是list-wise, 就用nDCG.

我的疑惑

1. session s 的rep由target得到,即 $rep(session)=f(target,other)$ 那么 target 与 图2中的 n 个item是什么关系? 论文有说each session with the contained item behaviors is treated as a list-wisw training sample,但还不是很清楚.
2. 为啥用搜索引擎的日志, 找个推荐数据集不是更直接么?

论文2,ListNet

loss定义

论文1的list-wise借鉴了参考2, ICML’2017的微软的论文.
定义 list-wise 的损失函数:
$$\sum _{i=1}^{m}L(y^{(i)},z^{(i)})\text{\hspace{1em}(1)}$$
where $m=|trainset|$ , $y^{(i)}=(y_1^{(i)},y_2^{(i)},...,y_{n^{(i)}}^{(i)})$, 是一个list,表示与query $q^{(i)}$ 相关的 $n^{(i)}$ 个文档的相关性得分. 与之类似, $z^{(i)}=(f(x_1^{(i)}),f(x_2^{(i)}),...,f(x_{n^{(i)}}^{(i)}))$ 是 ranking function $f(\cdot )$ 计算出的预估相关性.

probability model

图: permutation probability
对size=n的list作全排列, 有 $n!$ 种结果, 计算量不可接受, 也就是 NP_Hard? 所以提出 top one probability.

图: top one probability.

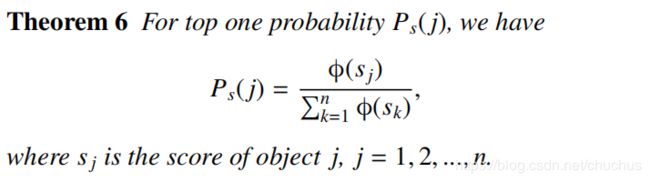
图: 定理6, doc j 排第一的概率描述

图: 对$\varphi (\cdot )$作指数函数定义后, 可以改写 定理6 , 就成了soft-max

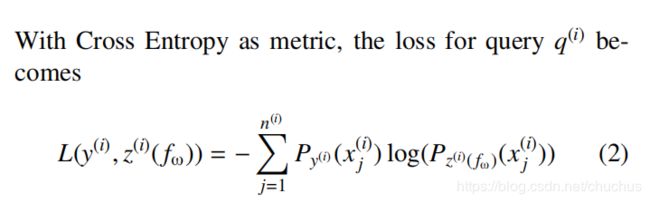
图: soft_max 得到 label与pred两个list的概率后, 用交叉熵作损失函数, 得到了最终的loss.

实验

• 数据集, 其中一个是CSearch, 来自商业搜索引擎.This data set provides five levels of relevance judgments, ranging from 4 (”perfect match”) to 0 (”bad match”).
• 指标,nDCG@5 and MAP(mean average precision).

思考讨论

• 所谓 list-wise
  所谓list-wise 也只是损失函数相关, 预测阶段依旧是point-wise打分并排序, 由此得到序列.
  谷歌的Seq2Slate的论文里有一段清晰的描述：

In listwise approaches the loss depends on the full permutation of items. Although these losses consider inter-item dependencies, the ranking function itself is pointwise, so at inference time the model still assigns a score to each item which does not depend on scores of other items (i.e., an item’s score will not change if it is placed in a different set).

• loss 与 常规多分类 有何异同
  已经很像了, recsys中召回任务的设计就可以是transformer那样的多分类. 但常规的label是one-hot(可能带有 label smooth), 此处是一个不那么陡峭的分布.

参考

1. CIKM’2017,alibaba,Session-aware Information Embedding for E-commerce Product Recommendation
2. ICML’2007,Learning to Rank: From Pairwise Approach to Listwise Approach