大话数据结构之AVL树

引言

AVL（Adelson-Velskii和E.M Landis）树，作为一种最老的平衡查找树，其本质仍然是一种二叉查找树，由于对于二叉查找树的多次删除操作，会导致左右子树失衡，失衡之后，我们并无法保证对树的操作保持在O(logN)的复杂度下，考虑一种极端情形，向一棵空的二叉查找树插入一个已经排序的序列[1,2,3,4,5,6]：

显然这种操作类似于链表（链表可以看成是特殊的二叉树）的插入，那么完成所有的节点的插入操作将花费O(N*N)的操作时间。查找任意一个节点，其消耗的时间也就是O(N)。
一种解决办法就是对于每个节点增加一个平衡的条件：任何节点的深度不能过深。AVL树的定义即是：对于一棵查找树，其每个节点的左右子树高度相差最大为1。那么对于上述那个极端情形的查找树，可以转化为如下情形：

至于这棵树是怎么得来的，后面就知道了。

AVL树旋转

显然，对于一棵AVL树进行插入操作的时候，可能会破坏某些节点的平衡条件（左右子树高度最大相差1），可以想象，只有那些属于插入节点开始到根节点那条路径上的节点的平衡条件才会改变，因为只有它们的子树的高度可能发生变化。所以，如果要保证插入之后的查找树依旧保持AVL特性，那么我们需要在这条路径上找到那个失衡的节点，并且重新平衡它。我们称这个重新平衡的动作为旋转（rotate）。
假设插入新节点X之后，导致某个节点R失衡，这个插入动作可能有以下四种情形：

1. R节点的左儿子的左子树进行了一次插入（LL）；
2. R节点的右儿子的右子树进行了一次插入（RR）；
3. R节点的左儿子的右子树进行了一次插入（LR）；
4. R节点的右儿子的左子树进行了一次插入（RL）；

根据对称性，1，2可以看成是一种情况；3，4也可以看成是一种情况。那么就是两种插入操作可能导致失衡。
对于1，2两种情况导致的失衡可以利用一次单旋转（single rotation）来完成平衡；3，4要复杂一些可以利用一次双旋转（double rotation）来完成平衡。

单旋转

回到前面那个极端情形，当插入1,2时，整个查找树还是平衡的，但是当插入3时，

1节点失衡（左子树高度为0，右子树高度为2），这显然是属于上面所说的四种情况的第2种（RR）。进行一次单旋转即可完成平衡，如何进行？将失衡节点1与其儿子节点2之间进行一次旋转：

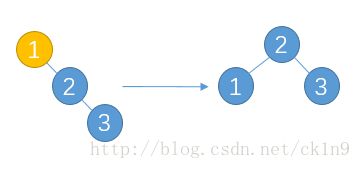
再插入4，没有问题，但是插入5会导致3节点失衡：

将失衡节点3与其儿子节点4进行一次旋转：

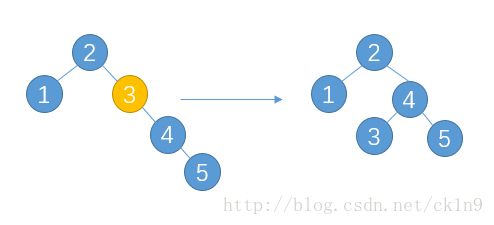
这里要注意的一点就是：当节点3与4旋转一次之后，4成为该子树的新节点，要注意的是不要忘记将2节点的右儿子重新指向新的4节点。
再插入节点6，会导致根节点2失衡：

在插入时要记得AVL树的两个特性（查找树/平衡）。
对于LL的情况，就不举例了，是一样的。

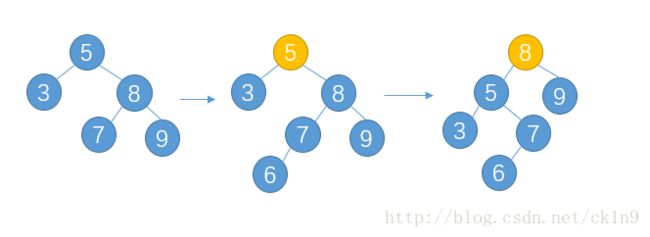
双旋转

考虑3，4两种情况：
如下面这个AVL树，

当插入新节点6的时候，会导致根节点5失衡，引起失衡的原因是在失衡节点5的右儿子的左子树进行了一次插入（RL），我们尝试采用单旋转的方式（在失衡节点5和其儿子8之间进行一次旋转），发现得到的新的查找树并不满足AVL特性（节点8仍旧是失衡的）。
为了重新得到平衡，节点8作为根的方式已经失败了，那么在插入节点到根节点的路径上（6，7，8，5），唯一的选择就是选择7作为新的根，如何进行呢？
考虑采用双旋转：首先，将失衡节点的儿子与其孙子进行一次旋转。即该例中的8和7：

我们发现，经过第一次旋转之后，得到的查找树虽然根节点还是失衡的，但是，发现它与RR的情况相同了！它相当于对于下面左边的AVL树进行了一次RR操作！

显然，对于上面的树再进行一次单旋转（失衡节点5与其新儿子7）即可完成最终的AVL树：

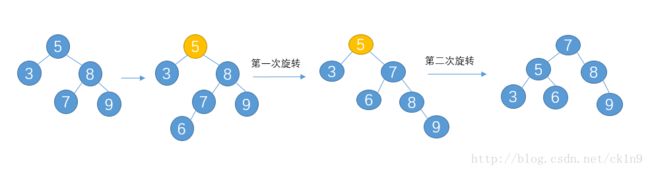
可以发现，双旋转就是先利用一次旋转将其转化为RR或者LL的情形，再利用一次单旋转完成最终的平衡。

代码实现

由于要比较节点的左右子树的高度，考虑将高度信息存储在树的节点中：

#define MAX(A,B) ((A>B)?(A):(B))
typedef enum notification
{
    LL,RR,LR,RL
}NOTIFY;
typedef int ElementType;
struct AvlNode;
typedef struct AvlNode * AvlTree;
typedef struct AvlNode * Position;
struct AvlNode
{
    ElementType data;
    AvlTree Left;
    AvlTree Right;
    int height;//记录节点的高度
    int counter;//懒惰删除 记录相同元素的个数
};

明显代码实现的重点是对于单旋转和多旋转的实现（其余操作如删除、插入、查找等都是类似于二叉查找树）。如前所述，可能导致整个AVL树失衡有4种情况（虽然存在对称现象，但是对于代码来说还是要分为4种，即LL,RR,LR,RL）。
考虑如下LL的一般情形：

考虑如下RR的一般情形：

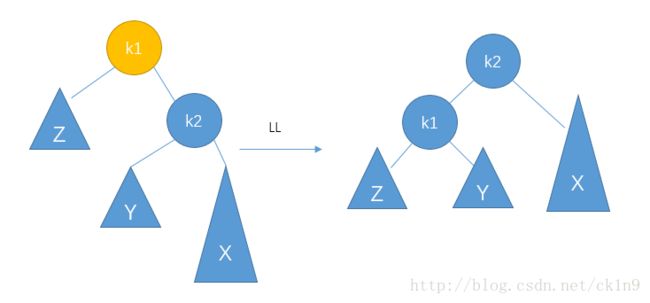
其中的转化关系其实就是链表的操作，要注意的就是完成旋转之后要更新节点中存储的高度信息。很容易写出如下代码：

AvlTree singleRotation(AvlTree node,NOTIFY id)
{
    AvlTree a=NULL, b=NULL;
    switch (id)
    {
    case LL:
        a = node;
        b = node->Left;
        a->Left = b->Right;
        b->Right = a;
        //旋转之后 记得更新新节点的高度！！！
        a->height = MAX(getHeight(a->Left), getHeight(a->Right));
        b->height = MAX(getHeight(b->Left), getHeight(b->Right));
        a = b;
        break;
    case RR:
        a = node;
        b = node->Right;
        a->Right = b->Left;
        b->Left = a;
        //旋转之后 记得更新新节点的高度！！！
        a->height = MAX(getHeight(a->Left), getHeight(a->Right));
        b->height = MAX(getHeight(b->Left), getHeight(b->Right));
        a = b;
        break;
    default:
        perror("error input\n");
        break;
    }
    return a;
}

如前面分析，双旋转即两次单旋转，第一次旋转是对失衡节点的儿子和孙子之间进行一次单旋转，第二次是对失衡节点与新儿子节点之间进行一次单旋转：

考虑如下一般的LR情形：

第一次旋转K2和K3相当于对于以K2为根节点的子树进行一次RR的单旋转，第二次对于K1和K3相当于对于整个树进行一次LL的单旋转。

考虑如下一般的RL情形：

第一次对于K2和K3进行旋转相当于对于以K2为根节点的子树进行一次LL的单旋转，第二次对于K1和K3相当于对整个树进行一次RR的单旋转。

得到如下代码：

AvlTree doubleRotation(AvlTree node,NOTIFY id)
{
    AvlTree a, b, c;
    switch (id)
    {
    case LR:
        node->Left = singleRotation(node->Left, RR);
        node = singleRotation(node, LL);
        break;
    case RL:
        node->Right = singleRotation(node->Right, LL);
        node = singleRotation(node, RR);
        break;
    default:
        perror("error input\n");
        break;
    }
    return node;
}

附上插入操作：（类似于二叉查找树的insert）

AvlTree AvlTreeInsert(AvlTree root, ElementType data)
{
    if (root == NULL)
    {
        root = (AvlTree)malloc(sizeof(struct AvlNode));
        if (!root)return NULL;
        root->data = data;
        root->height = 0;//我们设单个节点的高度为0
        root->Left = NULL;
        root->Right = NULL;//不要忘记左右儿子的初始化
        root->counter = 1;
    }
    else if (data < root->data)
    {
        root->Left = AvlTreeInsert(root->Left, data);
        //对于AVL树的一次插入可能导致某些节点失衡(插入的是左子树，那么肯定是左子树较高)
        if (getHeight(root->Left) - getHeight(root->Right) == 2)
        {
            if (data < root->Left->data)//LL
                root = singleRotation(root,LL);//单旋转 更换根节点
            else if (data > root->Right->data)//LR
                root = doubleRotation(root,LR);
        }
    }
    else if (data > root->data)
    {
        root->Right = AvlTreeInsert(root->Right, data);
        //对于AVL树的一次插入可能导致某些节点失衡(插入的是右子树，那么肯定是右子树较高)
        if (getHeight(root->Right) - getHeight(root->Left) == 2)
        {
            if (data > root->Right->data)//RR
                root = singleRotation(root,RR);//单旋转 更换根节点
            else
                root = doubleRotation(root,RL);//RL
        }
    }
    else
        root->counter++;
    root->height = MAX(getHeight(root->Left), getHeight(root->Right)) + 1;
    return root;
}

测试代码：（利用中序遍历输出AVL树，结果应该是递增序列）

void midTravesal(AvlTree root)
{
    if (!root)return;
    else
    {
        midTravesal(root->Left);
        printf("%d ", root->data);
        midTravesal(root->Right);
    }
}

int main(void)
{
    AvlTree root = NULL;
    for (int i = 1; i <= 6; i++)
        root = AvlTreeInsert(root, i);
    for(int i = 20;i>=7;i--)
        root = AvlTreeInsert(root, i);
    midTravesal(root);
    return 0;
}

输出结果为：

其余的操作都与二叉查找树类似，此处不再赘述。

总结

AVL是一种高度平衡的二叉树，每一次插入或者删除操作都要维护这种高度平衡，有时候这种代价是昂贵的。所以，后面将介绍一种与其类似的高级数据结构-红黑树。其应用范围要远大于AVL树。