强化学习之Q——learning
部分专有名词在上一篇文章有介绍,本文不作过多赘述。
目录
- 前言
- 算法思想
- 算法详解
- 算法公式
- 探险者寻宝藏实战(一维)
前言
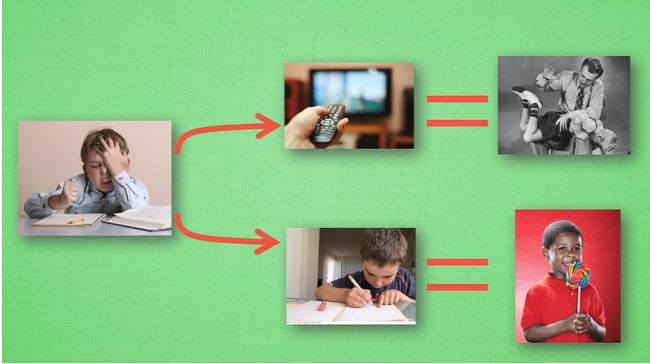
我们做事情都会有自己的一个行为准则,比如小时候爸妈常说“不写完作业就不准看电视”。所以我们在写作业的状态(state)下,好的行为就是继续写作业,直到写完它,我们还可以得到奖励(reward),不好的行为就是没写完作业就跑去看电视了,被爸妈发现就会被惩罚,这种事情做的多了,也变成了我们不可磨灭的记忆,这其实就是一个Q-learning的决策过程。
算法思想
Q-Learning是强化学习算法中value-based的算法,Q即为Q(s,a),就是在某一个时刻的state状态下,采取动作a能够获得收益的期望,环境会根据agent的动作反馈相应的reward奖赏,所以算法的主要思想就是将state和action构建成一张Q_table表来存储Q值,然后根据Q值来选取能够获得最大收益的动作。
Q-learning的主要优势就是使用了时间差分法(融合了蒙特卡洛和动态规划)能够进行off-policy的学习,使用贝尔曼方程可以对马尔科夫过程求解最优策略,本文对其中算法不进行推导,会另外写一篇推导的文章。

算法详解
我们还是用一开始举的做作业的例子来说明:

假设我们的行为准侧已经学习好了,现在我们处于状态s1,我在写作业,我有两个行为a1,a2,分别是看电视和写作业,根据我的经验(Q-table)知道,在s1的状态下,我选择a2写作业带来的reward奖赏比a1看电视高,在我的Q-table中,Q(s1,a1)=-2要小于Q(s1,a2)=1,所以我们判断要选择a2写作业作为我们的下一个行为。现在我们的状态更新成s2,我们还是有两个同样的选择,重复上面的过程,在行为准则Q-table中寻找Q(s2,a1)Q(s2,s2)的值,并比较他们的大小,选取较大的一个。接着根据a2我们到达s3并重复上述的决策过程,Q-learning的方法就是这样抉择的。那我们的Q-table这张行为决策表又是如何决策的呢?我们来看看。

回到之前的流程,根据Q表的估计,因为在s1中,a2的值比较大,通过之前的决策方法我们在s1选择了a2,并到达s2,这时我们开始更新用于决策的Q表,接着我们并没有在实际中采取任何行为,而是在想象自己在s2上采取了a1,a2两个行为,分别看看两种行为哪一个的Q值大,比如说Q(s2,a2)的值比Q(s2,a1)的大,所以我们把大的Q(s2,a2)乘上一个衰减值gamma(eg 0.9)并加上到达s2时所获得的奖励Reward(这里没有获取到我们的棒棒糖,所以奖励为0),因为会获取实实在在的奖励Reward,所以我们将这个作为我们现实中Q(s1,a2)的值,但是我们之前是根据Q表估计Q(s1,a2)的值。所以有了现实值和估计值,我们就可以更新Q(s1,a2)的值,变成新的值。但时刻记住,我们虽然用maxQ(s2)估算了一下s2的状态,但还没有在S2做出任何行为,s2的行为决策要等到更新完了以后再重新另外做,这就是off-policy的Q-learning是如何决策和学习优化决策过程。
算法公式

这一张图概括了我们之前所有的内容。这也就是Q-learning算法,每次更新我们都用到了Q现实和Q估计,而且Q-learning迷人之处就是在Q(s1,a2)的现实中,包含了一个**Q(s2)**的最大估计值,将对下一步衰减的最大估计和当前所得到的奖励作为这一步的现实。
参数介绍
Epsilon greedy:是用在决策上的一个策略,比如epsilon = 0.9的时候,就说明百分之90的情况我会按照Q表的最优值选择行为,百分之10的时间随机选择行为。alpha:学习率,决定这次的误差有多少是要被学习的。gamma:对未来reward的衰减值。gamma越接近1,机器对未来的reward越敏感
探险者寻宝藏实战(一维)
背景
在一个一维时间,在世界的右边有宝藏,探险者只要得到宝藏尝到了甜头,以后就会记住得到宝藏的方法,这就是他用强化学习所学习到的行为。
![]()
在这个游戏中,o所在的每个地点就是每个状态,而每个地点探险者所可以做出left/right两个行为,这就是探险者可以做出的action,而每种行为在每个状态下都会有一个值,也就是Q(s,a),如果在某个地点s1,探险者计算了Q(s1,a1)和Q(s1,a2),如果前者大于后者,那么探险者就会选择left这个行为,这就是行为准则。
预设参数
import numpy as np
import pandas as pd
import time
np.random.seed(2) # reproducible
N_STATES = 6 #一维世界的宽度
ACTIONS = ['left','right'] #探索者可用的动作
EPSILON = 0.9 #greedy贪婪度
ALPHA = 0.1 #学习率
GAMMA = 0.9 #奖励递减值
MAX_EPISODES = 13 #最大回合数
FRESH_TIME = 0.3 #每回合移动间隔时间
Q表
我们要将所有Q values放在q_table中,更新q_table也是在更新他的行为准则。q_table的index是所有对应的state(o所在的位置),columns是对应的action(探险者选择left或者right)
def build_q_table(n_states, actions):
table = pd.DataFrame(
np.zeros((n_states, len(actions))), # q_table 全 0 初始
columns=actions, # columns 对应的是行为名称
)
return table
# q_table:
"""
left right
0 0.0 0.0
1 0.0 0.0
2 0.0 0.0
3 0.0 0.0
4 0.0 0.0
5 0.0 0.0
"""
定义action
接着定义探险者是如何挑选行为的,这就是我们引入epsilon greedy的概念。因为在初始阶段,随机的探索环境,往往比固定的行为模式要好,所以这也是累积经验的阶段,我们希望探险者不那么贪婪(greedy),所以EPSILON就是用来控制贪婪程度的值。EPSILON可以随着探险时间不断提升(越来越贪婪),不过在这个例子中,我们就固定EPSILON=0.9,90%的时间是选择最优策略,10%的时间来探索。
def choose_action(state, q_table):
state_actions = q_table.iloc[state, :] # 选出这个state的所有 action的value值
if (np.random.uniform() > EPSILON) or (state_actions.all() == 0): #非贪婪 or 或者这个 state 还没有探索过
action_name = np.random.choice(ACTIONS)
else:
action_name = state_actions.idxmax() # 贪婪模式
return action_name
环境的反馈S_,R
做出行为后,环境也要给我们的行为一个反馈,反馈出下一个state(S_)和上一个state(S)做出action(A)所得到的reward(R)。这里定义的规则是,只有当o移动到了T(探险者获取了宝藏),探险者才会得到唯一的奖励,奖励值R=1,其他情况没有奖励。
def get_env_feedback(S,A):
if A== 'right': #往右探险
if S == N_STATES - 2: #找到宝藏
S_ = 'terminal'
R = 1
else:
S_ = S + 1
R = 0
else: #往左探险
R = 0
if S == 0:
S_ = S #碰壁
else:
S_ = S - 1
return S_,R
环境更新
接下来就是环境的更新了,这里不多赘述。
def update_env(S, episode, step_counter):
env_list = ['-']*(N_STATES-1) + ['T'] # '---------T' our environment
if S == 'terminal':
interaction = 'Episode %s: total_steps = %s' % (episode+1, step_counter)
print('\r{}'.format(interaction), end='')
time.sleep(2)
print('\r ', end='')
else:
env_list[S] = 'o'
interaction = ''.join(env_list)
print('\r{}'.format(interaction), end='')
time.sleep(FRESH_TIME)
强化学习的主循环
最重要的地方就是这里,将刚才理论部分我们讲解到的算法实现出来。
def rl():
q_table = bulid_q_table(N_STATES,ACTIONS) #初始化q_table
for episode in range(MAX_EPISODES): #回合
step_counter = 0
S = 0 #回合初始的位置
is_terminated = False
update_env(S,episode,step_counter) #环境更新
while not is_terminated:
A = choose_action(S,q_table) #选择行为
S_,R = get_env_feedback(S,A) #实施行为并得到环境的反馈
q_predict = q_table.loc[S,A] #估算的(状态-行为)值
if S_ != 'terminal':
q_target = R + GAMMA*q_table.iloc[S_,:].max() #实际的(状态-行为)值
else:
q_target = R #实际的(状态-行为值)
is_terminated = True
q_table.loc[S,A] += ALPHA*(q_target - q_predict) #q_table更新
S = S_ #更新探索者位置
update_env(S,episode,step_counter+1)
step_counter += 1
return q_table
结果
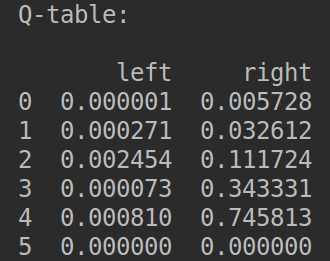
我们可以看到,一开始没有任何经验的探险者需要非常多次的尝试才能找到宝藏,而随着探险次数的增多,最后就可以自己走到宝藏的地方了。
![]()
![]()
参考:
https://github.com/MorvanZhou