使用 KNIME 和 Spark 进行时间序列分析

需求预测

我认为我们都同意，知道未来会发生什么使生活更加轻松。 对于生活事件，洗衣机和冰箱的价格或整个城市的电能需求而言，都是如此。 知道明天或下周需要多少瓶橄榄油，可以在零售商店中制定更好的进货计划。 了解汽油或柴油价格可能上涨的情况，可使货运公司更好地计划其财务状况。 这种知识可以提供帮助的例子数不胜数。

需求预测是数据科学的一大分支。 其目标是使用历史数据和可能的其他外部信息来估计未来需求。 需求预测可以涉及任何数字：餐馆的访客、产生的kW / h、学校新注册、商店货架上所需的啤酒瓶、家电价格等。

预测纽约的出租车需求

作为需求预测的一个示例，我们将解决预测纽约市出租车需求的问题。 在纽约这样的大城市中，每天有超过13,500辆黄色出租车在街上漫游（根据《 2018年出租车和豪华轿车委员会概况》 ）。 这使得了解和预测出租车需求对于出租车公司乃至城市规划者而言都是至关重要的任务，以提高出租车队的效率并最大程度地减少旅行之间的等待时间。

在本案例研究中，我们使用了纽约出租车数据集 ，该数据集可从纽约出租车和豪华轿车委员会（TLC）网站下载。 该数据集跨越纽约市的出租车旅行10年，其中包含有关每次旅行的广泛信息，例如上车和下车的日期/时间，位置，票价，小费，距离和乘客人数。 由于我们仅将本案例研究用于演示，因此我们仅使用了2017年的Yellow出租车子集。对于更一般的应用，将另外几年的数据包括到数据集中将很有用，至少能够估算年度季节性。

让我们设置本教程的目标，以预测下一个小时在纽约市所需的出租车行程。

时间序列分析：过程

需求预测问题是经典的时间序列分析问题。 我们有一个时间序列的数值（价格，访问者数量，kW / h等），并且我们希望根据过去的N个值来预测下一个值。 在我们的案例中，我们有一个每小时的出租车旅行次数的时间序列（图1a），并且我们要根据最近N个小时的出租车旅行次数来预测下一个小时的出租车请求次数。

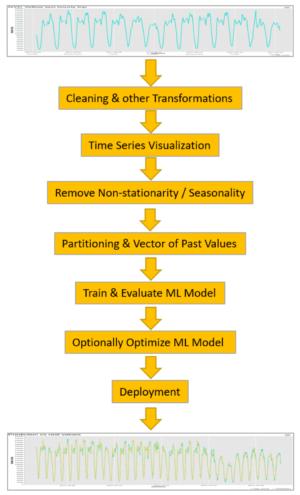
对于此案例研究，我们通过以下步骤实现了时间序列分析过程 （图1）：

• 数据转换：聚合、时间对齐、缺失值估算和其他所需的转换，通常取决于数据域和业务案例
• 时间序列可视化
• 消除非平稳/季节性（如果有）
• 数据分区以构建训练集（过去）和测试集（未来）
• N个过去值的向量的构造
• 训练一个或多个机器学习模型以实现数值输出
• 预测误差的计算
• 模型部署（如果可以接受预测误差）

图1.时间序列分析的一些经典步骤。

请注意，单个数值的精确预测可能是一项复杂的任务。 在某些情况下，甚至不需要精确的数值预测，并且在将其转换为分类问题后，可以令人满意且容易地解决相同的问题。 为了将数字预测问题转化为分类问题，您只需要在目标变量之外创建类。

例如，很难预测两周后的洗衣机价格，但是预测此价格在两周内会增加，减少还是保持不变则容易得多。 在这种情况下，我们已将价格预测的数值问题转换为具有三个类别（价格上涨、价格下跌、价格不变）的分类问题。

数据清理和其他转换

第一步是从时间稀疏的原始数据行（在这种情况下为出租车出行，但可能是与客户签订合同或快速傅立叶变换幅度相同），然后按时间序列采样值。 这通常需要两件事：

• 在预定义的时间范围内的聚合操作：秒、分钟、小时、天、周或月，具体取决于数据和业务问题。 用于聚合的粒度（时间标度）对于可视化不同的季节性影响或捕获信号中的不同动态非常重要。

• 重新对齐操作，以确保在所考虑的时间窗口内时间采样是均匀的。 通常，时间序列以捕获的时间的单个序列表示。 如果缺少任何时间样本，我们不会注意到。 重新调整过程会在跳过的采样时间插入缺失值。

另一个经典的预处理步骤包括估算缺失值。 这里有许多时间序列专用技术，例如使用上一个值、上一个和下一个值之间的平均值或上一个和下一个值之间的线性插值。

此处的目标是预测下一个小时的出租车需求（等于所需的出租车行程数）。 因此，由于我们需要时间序列的每小时时间标度，因此在数据集中按每天的每一小时计算纽约市的出租车旅行总数。 这要求按小时和日期（年，月，月中的某天，小时）对数据进行分组，然后对每组中的行数（即出租车行程数）进行计数。

时间序列可视化

在继续进行数据准备，模型训练和模型评估之前，通过可视化数据探索了解我们正在处理的问题总是很有用的。 在这种情况下，我们将在多个时间范围内可视化数据。 每个可视化可以提供有关数据时间演变的不同见解。

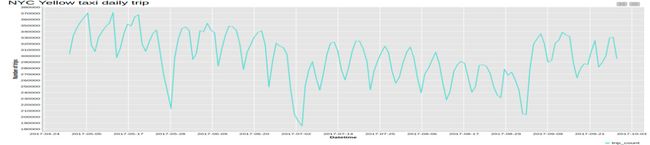
在上一步中，我们已经按小时汇总了出租车行程数。 这将产生时间序列x（t） （图2a）。 此后，为了观察不同时间尺度上的时间序列演变，我们还在按天（图2b）和按月（图2c）进行汇总后将其可视化。

从每小时时间序列的图上，您可以清楚地看到24小时制：白天出租车次数较多，而夜间出租车次数较少。

如果我们改用每日量表，则每周的季节性模式将变得明显，工作日的出行次数增加，周末的出行次数减少。 通过变化的平均值，可以轻松地在此时间刻度上发现此时间序列的非平稳性。

最后，每月时间序列的图没有足够的数据点来显示任何类型的季节性模式。 将数据集扩展到包括更多年可能会在图中产生更多点，并且可能会观察到冬季/夏季的季节性模式。

  图2a。 根据纽约出租车数据集，2017年6月的前两周将纽约市按小时计的出租车旅行次数绘制成图。 这里的24小时季节性很容易看到。

图2b。 根据纽约市出租车数据集，放大了2017年5月至2017年9月之间的时间范围，按天划分了纽约市出租车行车次数的图。 这里的每周季节性非常容易发现。 三个深谷分别对应于阵亡将士纪念日、七月四日和劳动节。图2c。 根据NYC Taxi数据集，绘制了2017年全年纽约市出租车行车次数。 您可以看到冬天（出租车旅行次数更多）和夏天（出租车旅行次数更少）之间的区别。

图2a。 根据纽约出租车数据集，2017年6月的前两周将纽约市按小时计的出租车旅行次数绘制成图。 这里的24小时季节性很容易看到。

图2b。 根据纽约市出租车数据集，放大了2017年5月至2017年9月之间的时间范围，按天划分了纽约市出租车行车次数的图。 这里的每周季节性非常容易发现。 三个深谷分别对应于阵亡将士纪念日、七月四日和劳动节。

图2c。 根据NYC Taxi数据集，绘制了2017年全年纽约市出租车行车次数。 您可以看到冬天（出租车旅行次数更多）和夏天（出租车旅行次数更少）之间的区别。

非平稳性、季节性和自相关函数

许多时间序列分析技术的常见要求是数据必须是固定的 。

平稳过程具有以下特性：均值、方差和自相关结构不会随时间变化。 平稳性可以用精确的数学术语定义，但就我们的目的而言，我们指的是没有时间趋势的平坦时间序列，其平均值和方差随时间变化，而自相关结构随时间变化。 出于实用目的，通常从运行序列图或线性自相关函数（ ACF ）确定平稳性。

如果时间序列是非平稳的，我们通常可以通过将其替换为一阶差分来将其转换为平稳的。 也就是说，给定序列x（t） ，我们创建新的序列y（t）= x（t）-x（t-1） 。 您可以多次对数据进行差异处理，但是通常一阶差异就足够了。

季节性违反平稳性，并且通常也从时间序列的线性自相关系数确定季节性。 这些被计算为Pearson相关系数在时间t-1的时间序列x（t）的值之间的在时间t和它的过去值，...，TN。 通常，在-0.5到0.5之间的值将被认为是低相关性，而超出此范围（正或负）的系数将表明高相关性。

实际上，我们使用ACF图来确定主要季节性或非平稳性的指数。 ACF图在y轴上报告针对x（t）及其过去的x（ti）值计算的自相关系数与在x轴上的滞后i的关系。 ACF图中的第一个局部最大值定义了季节性模式的滞后（lag = S）或对非平稳性进行校正的需要（lag = 1）。 为了不考虑不相关的局部最大值，通常会引入截止阈值，通常是从预定义的置信区间（95％）开始。 同样，更改时间范围（即聚合的粒度）或延长时间窗口使我们能够发现不同的季节性模式。

如果我们发现季节性滞后为S ，则可以应用多种不同的技术来消除季节性。 我们可以从所有后续的S样本窗口中删除前S个样本； 我们可以计算一部分数据集的平均S样本模式，然后从随后的所有S样本窗口中删除该模式； 我们可以训练机器学习模型来重现要删除的季节性模式； 或更简单地说，我们可以从当前值x（t）中减去先前的值x（tS） ，然后处理残差y（t）= x（t）-x（tS）。 为了使本教程保持简单，我们在本教程中选择了最后一种方法。

图3显示了出租车每小时行驶次数的时间序列的ACF图。 y轴上是为x（t）计算的自相关系数及其在滞后小时1到50的先前值。在x轴上是滞后小时。 该图表显示了出租车业务所期望的滞后= 1和滞后= 24（即每日季节性）的峰值。 最高正相关系数在x（t）和x（t-1） （0.91）之间， x（t）和x（t-24） （0.83）之间，然后是x（t）和x（t-48）之间 （0.68）。

如果我们使用时间序列的每日汇总，并在n> 7的滞后区间上计算自相关系数，我们还将在第7天观察到峰值，即每周的季节性。 从更大的范围来看，我们可能会观察到冬季和夏季的季节性变化，冬季乘车的人比夏季乘车的人更多。 但是，由于我们仅考虑一年的数据，因此我们不会检查这种季节性。

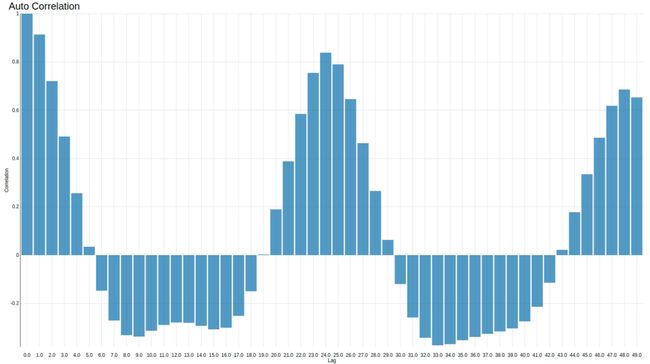图3. 50小时内的自相关图（皮尔森系数）。 x（t） 与 x（t-1） ， x（t-24） 和 x（t-48） 的最强相关性，表示每天24小时的季节性。

数据分区以构建训练集和测试集

此时，必须将数据集划分为训练集（过去）和测试集（未来）。 请注意，两组之间的分割必须是时间上的分割。 不要使用随机分区，而是按时间顺序分割！ 这是为了避免数据从训练集（过去）泄漏到测试集（未来）中。

我们为训练集保留了2017年1月至2017年11月的数据，为测试集保留了2017年12月的数据。

滞后：过去N个值的向量

该用例的目的是预测下一个小时纽约市的出租车旅行需求。 为了进行此预测，我们需要前N个小时的出租车行程需求。 对于时间序列的每个值x（t） ，我们要构建向量x（tN），…，x（t-2），x（t-1），x（t）。 我们将过去的值x（tN），…，x（t-2），x（t-1）用作模型的输入，而将当前值x（t）用作目标列以训练模型。 对于此示例，我们尝试了两个值：N = 24和N = 50。

原文链接: https://www.infoworld.com/article/3405256/time-series-analysis-with-knime-and-spark.html