二元函数 是 z = f ( x, y ) , 或者 f ( x, y, z ) = 0 ,
比如, z = f ( x, y ) , 有 2 个 自变量 x, y, 有 1 个 因变量 y, 这是 二元函数 。
或者, f ( x, y, z ) = 0 , 这种, 跟 z = f ( x, y ) 也 差不多, 可以叫 二元隐函数 。
不过 , f ( x, y, z ) = 0 是 一个方程, 和 x, y 对应 的 z 可能 不止一个, 这是 和 z = f ( x, y ) 的 区别 。
比如 , 球面 x ² + y ² + z ² = r ² , r 为常量 , 是一个 方程, 也是 隐函数 。
z = 根号 ( r² - x ² - y ² ) 就是 半个球面, 另外 半个球面 是 z = - 根号 ( r ² - x ² - y ² ) 。
总之呢, 把 ( x, y ) 的 集合 看作 p 的 集合, p 是一个 ( x, y, 0 ) 处 的 点, 0 是 z 坐标 。
z = f ( x, y ) 可以看作 写成 z = f ( p ) ,
给 p 指定 一个 定义域, 这个 定义域 是 xy 平面 上 的 一个 区域, 也 可以说 是 一个 平面图形,
则 在 定义域 内, z = f ( p ) 的 极值点 在哪里, 有几个 ?
z = f ( p ) 是 定义域 上方(下方) 的 曲面, 极值点 就是 曲面 上 的 峰顶 和 谷底 。
这个 问题 也和 霍奇猜想 有关 。
z = f ( p ) 的 定义域 是 二维平面 上 的 一个 区域, 这种 函数 称为 二维自变量 函数 。 这种 函数 的 自变量 是一个 元组 ( x, y ) , p = ( x, y ) 。
同理, 可以有 三维自变量 函数, 比如 a = f ( p ) , p = ( x, y, z ) 。
还可以有 四维自变量函数, 五维自变量函数, …… , n 维自变量函数 。
z = f ( p ) 是 一个 二维自变量函数, 也是 一个 二元函数, 用哪个叫法都可以 。
z = f ( p ) 是 三维坐标系 里 的 一个 曲面, 可以想象, 以 xy 平面 为 “底面”, 曲面 在 z 方向上 高低起伏, 就像是 喀斯特地貌 上 的 一个个 小山峰, 这些 小山峰 的 顶点 就是 极值点 。
用 直观 和 逻辑 分析一下, 可以知道, 作一些 平面, 垂直于 xy 平面, 这些 平面 过 小山峰 的 顶点 和 曲面 相交, 得到 的 相交线 称为 垂面交线, 垂面交线 也是 函数曲线 。 对于 每条 垂面交线, 小山峰 的 顶点 就是 垂面交线 的 极值点 。
即, 曲面 的 极值点 也是 过 该 极值点 的 每一条 垂面交线 的 极值点 。
进一步, 可以发现, 如果 曲面 上 的 一点 不是 极值点, 则 过 该点 任意 取 两条 垂面交线, 该点 必然 不会同时 是 这两条 垂面交线 的 极值点 。
反过来, 可以说, 过 曲面 上 的 一点 取 任意 两条 垂面交线, 若 该点 对 两条 垂面交线 都是 极值点, 则 该点 是 曲面 的 极值点 。
也可以说, 过 曲面 上 的 一点 取 任意 两条 垂面交线, 若 该点 是 两条 垂面交线 的 极值点, 则 该点 是 曲面 的 极值点 。
这可以 称为 二元函数极值定理 。
二元函数极值定理 表示 曲面 上 两条 垂面交线 可以 决定 曲面 的 极值点, 曲面 上 两条 垂面交线 相交, 若 交点 是 两条 垂面交线 的 极值点, 则 交点 是 曲面 的 极值点 。
垂面 垂直于 xy 平面, 可以平行于 xz 平面 或 yz 平面 。 我们可以让 两个垂面 一个 平行于 xz 平面, 一个 平行于 yz 平面, 此时, 二元函数极值定理 可以写成 偏导数 的 形式 :
对于 二元函数 z = f ( x, y ) , 若 ( X₀, Y₀ ) 处 的 偏导数 ∂ z / ∂ x = 0 且 ∂ z / ∂ y = 0 , 则 ( X₀, Y₀ ) 处 是 曲面 的 极值点 。
也可以 严格一点 表达, 对于 二元函数 z = f ( x, y ) , 当 x = X₀, y = Y₀ 时, 若 偏导数 ∂ z / ∂ x = 0 且 ∂ z / ∂ y = 0 , 则 ( X₀, Y₀, z ) 是 极值点 。
嗯 …… 看来 偏导数 还是 有点用的 。
进一步, 可以推想, 对于 n 元函数, 极值条件 和 上述 的 二元函数 的 情形 也是 类似 的, 可以 表达为 :
对于 n 元函数, y = f ( x1, x2, x3, …… , xn ) , 若 在 ( X1, X2, X3, …… , Xn ) 处, 满足 以下 方程组 :
∂ y / ∂ x1 = 0
∂ y / ∂ x2 = 0
∂ y / ∂ x3 = 0
……
∂ y / ∂ xn = 0
则 ( X1, X2, X3, …… , Xn ) 处 是 y 的 极值点 。
这 称为 n 元函数极值定理 。
应该指出, 满足 二元函数极值定理 和 n 元函数极值定理 的 点 不一定 是 极值点, 也有可能是 驻点 (又称为平稳点、稳定点或临界点), 可以参考 一元函数 驻点(又称为平稳点、稳定点或临界点) 的 概念 。
可以 用 一个 图 简单 的 看一下 一元函数 的 极值点 和 驻点 :
三维曲面 和 高维曲面 上 的 驻点 的 情形 比 二维曲线(一元函数) 的 驻点 更复杂一些 。 可以把 z = sin x + sin y 的 曲面 画出来 看看 。
我在 《关于 牛顿 一个晚上 搞定 最速降线》 https://www.cnblogs.com/KSongKing/p/12944582.html 的 文末 留 的 那道题 也可以看作 一个 二元函数极值问题 。
那道题 是 这样 :
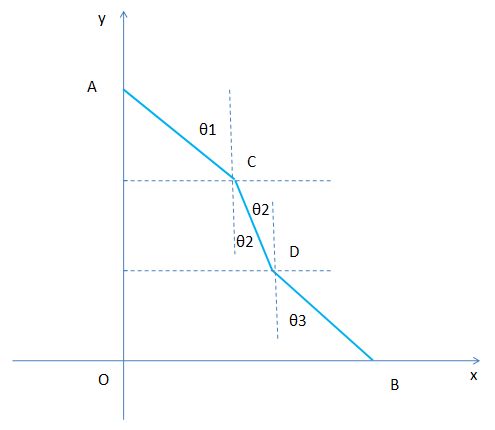
如图, 光线 从 A 点 出发, 沿 AC 以 速度 v1 到达 C 点, 沿 CD 以 速度 v2 到达 D 点, 沿 DB 以 速度 v3 到达 B 点,
A 点坐标 是 ( 0, 3h ) , B 点 坐标 是 ( L, 0 ) , C 点 坐标 是 ( xc, 2h ) , D 点 坐标 是 ( xd, h ) , h 、L 为 常量 。
问 C 点 D 点 的 横坐标 xc 、xd 是 多少 时, 光 从 A 到 B 的 时间 最短 ?
这个题 在 本文 里 命名为 题 (1) 。
可以用 二元函数极值 的 思路 来 做这个题 :
可以把 A 、B 、C 、D 四 个 点 的 坐标 改为 ( Xa, Ya ) 、( Xb, Yb ) 、( xc, Yc ) 、( xd, Yd ) , xc, xd 为 变量, Xa, Ya, Xb, Yb, Yc, Yd 为 常量 。
为了便于叙述, 把 A 点 、B 点 、 C 点 、 D 点 的 y 坐标 记为 Ya, Yb, Yc, Yd, 原来 是 3h, 0, 2h, h , 实际上, 到最后, 会发现 结论 和 y 坐标 的 具体取值 没有关系 。
设 光 从 A 沿 AC - CD - DB 路径到达 B 的 时间 为 t ,
t = AC / v1 + CD / v2 + DB / v3
= 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] / v1 + 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] / v2 + 根号 [ ( Xb - xd ) ² + ( Yb - Yd ) ² ] / v3
t = 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] / v1 + 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] / v2 + 根号 [ ( Xb - xd ) ² + ( Yb - Yd ) ² ] / v3 (1) 式
光 从 A 到 B 的 时间最短 就是 t 取 最小值, 这是 t 的 极值问题 。
(1) 式 中 xc, xd 为 自变量, t 为 因变量, 其它 为 常量 。 求 xc, xd 取什么值时, t 取极值 。
t 是 xc 、xd 的 函数, 记为 t = f ( xc, xd ) , 这是一个 二元函数 。
根据 二元函数极值定理, 可以列方程组 :
∂ t / ∂ xc = 0 1-1 式
∂ t / ∂ xd = 0 1-2 式
为了便于叙述, 这个 方程组 称为 方程组 (1), 方程组 (1) 的 解 就是 t 的 极值条件 。
1-1 式 可得 :
∂ { 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] / v1 + 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] / v2 + 根号 [ ( Xb - xd ) ² + ( Yb - Yd ) ² ] / v3 } / ∂ xc = 0
∂ { 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] / v1 } / ∂ xc + ∂ { 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] / v2 } / ∂ xc + ∂ { 根号 [ ( Xb - xd ) ² + ( Yb - Yd ) ² ] / v3 } / ∂ xc = 0
∂ { 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] / v1 } / ∂ xc + ∂ { 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] / v2 } / ∂ xc + 0 = 0
∂ { 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] / v1 } / ∂ xc + ∂ { 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] / v2 } / ∂ xc = 0
1 / v1 * 1/2 * 1 / 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] * ( 2 xc - 2 Xa ) + 1 / v2 * 1/2 * 1 / 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] * ( 2 xc - 2 xd ) = 0
1 / v1 * ( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] + 1 / v2 * ( xc - xd ) / 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] = 0
1 / v1 * ( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] - 1 / v2 * ( xd - xc ) / 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] = 0
1 / v1 * ( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] = 1 / v2 * ( xd - xc ) / 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] (2) 式
因为
( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( Yc - Ya ) ² ] = sin θ1
( xd - xc ) / 根号 [ ( xd - xc ) ² + ( Yd - Yc ) ² ] = sin θ2
所以, (2) 式 可化为 :
sin θ1 / v1 = sin θ2 / v2
同理, 1-2 式 可得 sin θ2 / v2 = sin θ3 / v3 , 于是
sin θ1 / v1 = sin θ2 / v2 (3) 式
sin θ2 / v2 = sin θ3 / v3 (4) 式
这就是 方程组 (1) 的 解 , 也就是 t 的 极值条件, 也就是 本题 答案, 当 满足 (3) 式 (4) 式 时, 光 从 A 到 B 的 时间 最短 。
其实 极值点 的 意义 是 峰值 谷值, 极值点 可能 不止 一个, 极值点 也不一定 是 最大值 最小值, 但 这些问题 我们暂不考虑, 在 下文 里 也一样 。
接下来, 我们来解 最速降线 问题 。 这个课题 在 本文 命名为 题 (2) 。
如图, 已知 A 、B 两点, A 、B 的 位置 确定 。 A 点 坐标 是 ( Xa, Ya ) , B 点 坐标 是 ( Xb, Yb ) 。
和 伯努利推导法 一样, 在 A 、B 之间 的 y 方向 上 分为 等高 的 n + 1 层, , n -> 无穷,
由 机械能守恒 可知, 小球 从 A 点 滚落, 在 ( x, y ) 处 的 速度 v = V ( x, y ) = 根号 [ 2 g ( Ya - y ) ] ,
在 每一层 的 分界线 取一个 点, 可得 n 个 点 P1, P2, P3 …… Pn , 按 A, P1, P2, P3 …… Pn, B 这样 的 顺序 把 这些点 连起来, 可以 构成 一条 从 A 到 B 的 路径, 称为 APB 。
让 小球 沿 APB 路径 从 A 滚动 到 B, 求 当 P1, P2, P3 …… Pn 点 的 x 坐标 是 多少时, 小球 从 A 到 B 的 时间 最短 。
记 P1, P2, P3 …… Pn 的 坐标 为 ( x1, y1 ), ( x2, y2 ), ( x3, y3 ) …… ( xn, yn ) ,
规定 小球 从 A 到 P1 的 速度 是 V ( x1, y1 ) , 从 P1 到 P2 的 速度 是 V ( x2, y2 ) , 从 P2 到 P3 的 速度 是 V ( x3, y3 ) …… 以此类推 。
总之 就是 小球 从 第 n - 1 个 点 滚到 第 n 个 点 的 速度 是 V ( xn, yn ) 。
小球 最后 从 Pn 滚动 到 B 的 速度 是 V ( Xb, Yb ) 。
记
v1 = V ( x1, y1 )
v2 = V ( x2, y2 )
v3 = V ( x3, y3 )
……
vn = V ( xn, yn )
vb = V ( xb, yb )
设 小球 沿 APB 路径 从 A 滚动 到 B 的 时间 为 t,
t = AP1 / v1 + P1P2 / v2 + P2P3 / v3 + …… + PnB / vb
AP1 / v1 = 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² ] / v1
P1P2 / v2 = 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² ] / v2
P2P3 / v3 = 根号 [ ( x3 - x2 ) ² + ( y3 - y2 ) ² ] / v3
……
PnB / vb = 根号 [ ( Xb - xn ) ² + ( Yb - yn ) ² ] / vb
Xa, Ya, Xb, Yb 为 常量, y1, y2, y3 …… yn 为 常量, x1, x2, x3 …… xn 是 变量 。
可以看到 , t 是 x1, x2, x3 …… xn 的 函数, 可以记为 t = f ( x1, x2, x3 …… xn ) , 是一个 多元函数 。
小球 从 A 到 B 的 时间最短 就是 t 的 极值, 根据 n 元函数极值定理 , 可以 列方程组 :
∂ t / ∂ x1 = 0 2-1 式
∂ t / ∂ x2 = 0
∂ t / ∂ x3 = 0
……
∂ t / ∂ xn = 0
这个方程组 称为 方程组 (2) 。
先 化简 2-1 式 ,
∂ t / ∂ x1 = 0
∂ { AP1 / v1 + P1P2 / v2 + P2P3 / v3 + …… + PnB / vb } / ∂ x1 = 0
∂ ( AP1 / v1 ) / ∂ x1 + ∂ ( P1P2 / v2 ) / ∂ x1 + ∂ ( P2P3 / v3 ) / ∂ x1 + …… + ∂ ( PnB / vb ) / ∂ x1 = 0 (5) 式
因为 P2P3, v3, P3P4, v4, P4P5, v5 …… PnB, vb 和 x1 无关, 所以
∂ ( P2P3 / v3 ) / ∂ x1 = 0
∂ ( P3P4 / v4 ) / ∂ x1 = 0
∂ ( P4P5 / v5 ) / ∂ x1 = 0
…… = 0
∂ ( PnB / vb ) / ∂ x1 = 0
于是, (5) 式 得 :
∂ ( AP1 / v1 ) / ∂ x1 + ∂ ( P1P2 / v2 ) / ∂ x1 + 0 + …… + 0 = 0
∂ ( AP1 / v1 ) / ∂ x1 + ∂ ( P1P2 / v2 ) / ∂ x1 = 0
∂ { 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² ] / v1 } / ∂ x1 + ∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² ] / v2 } / ∂ x1 = 0
因为 v1 = V ( x1, y1 ) = 根号 [ 2 g ( Ya - y1 ) ] , 可以看到, v1 和 x1 无关, 或者说, 对于一个 确定 的 y1, 无论 x1 如何变化, v1 不变, 所以, 相对于 x1, v1 为 常量, 可以 提到 偏导符号 ∂ { } 外面 来 。 v2 也是 同样 。
接下来 的 推导过程 和 方程组 (1) 的 1-1 式 类似, 同理可得 :
1 / v1 * ( x1 - Xa ) / 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² ] = 1 / v2 * ( x2 - x1 ) / 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² ]
sin θ1 / v1 = sin θ2 / v2
方程组 (2) 的 其它 方程 同理 可得 :
sin θ2 / v2 = sin θ3 / v3
sin θ3 / v3 = sin θ4 / v4
sin θ4 / v4 = sin θ5 / v5
……
sin θn / vn = sin θb / vb
即 sin θ1 / v1 = sin θ2 / v2 = sin θ3 / v3 = …… = sin θn / vn = sin θb / vb = C , C 为常量
写成通式 sin θ / v = C , C 为常量
啊, 这, 算是 证明了 最速降线 的 每个 微元 都 满足 斯涅耳定理(折射定律) ?
再来看一个题 , 这个题 在 本文 命名为 题 (3) 。
如图, A 、B 两点 固定, C 、D 两点 位置任意, 按 A 、C 、D 、B 的 顺序 把 4 个 点 连起来, 可以构成一条 从 A 到 B 的 路径, 称为 ACDB 。
问 C 、D 的 位置 为何 时, 路径 ACDB 最短 ?
设 ACDB 长度 为 L, A、B、C、D 的 坐标 为 ( Xa, Ya ) 、( Xb, Yb ) 、( xc, yc ) 、( xd, yd ) 。
L = AC + CD + DB
= 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] + 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] + 根号 [ ( Xb - xd ) ² + ( Yb - yd ) ² ]
L = 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] + 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] + 根号 [ ( Xb - xd ) ² + ( Yb - yd ) ² ]
Xa, Ya, Xb, Yb 为 常量, xc, yc, xd, yd 为 变量 。
L 是 xc, yc, xd, yd 的 函数, 可以记为 L = f ( xc, yc, xd, yd ) , 是 一个 四元函数 。
根据 n 元函数极值定理, L 的 极值条件 是 以下 方程组 :
∂ L / ∂ xc = 0 3-1 式
∂ L / ∂ yc = 0 3-2 式
∂ L / ∂ xd = 0 3-3 式
∂ L / ∂ yd = 0 3-4 式
这个 方程组 称为 方程组 (3) 。
化简 3-1 式 :
∂ { 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] + 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] + 根号 [ ( Xb - xd ) ² + ( Yb - yd ) ² ] } / ∂ xc = 0
∂ { 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] } / ∂ xc + ∂ { 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] } / ∂ xc + ∂ { 根号 [ ( Xb - xd ) ² + ( Yb - yd ) ² ] } / ∂ xc = 0
∂ { 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] } / ∂ xc + ∂ { 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] } / ∂ xc + 0 = 0
∂ { 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] } / ∂ xc + ∂ { 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] } / ∂ xc = 0
1/2 * 1 / 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] * ( 2 xc - 2 Xa ) + 1/2 * 1 / 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] * ( 2 xc - 2 xd ) = 0
( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] + ( xc - xd ) / 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] = 0
( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] - ( xd - xc ) / 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ] = 0
( xc - Xa ) / 根号 [ ( xc - Xa ) ² + ( yc - Ya ) ² ] = ( xd - xc ) / 根号 [ ( xd - xc ) ² + ( yd - yc ) ² ]
sin θ1 = sin θ2
同理, 3-2 式 可得 : cos θ1 = cos θ2
3-3 式 可得 : sin θ2 = sin θ3
3-4 式 可得 : cos θ2 = cos θ3
于是, 方程组 (3) 的 解 是 :
sin θ1 = sin θ2 (6) 式
cos θ1 = cos θ2 (7) 式
sin θ2 = sin θ3 (8) 式
cos θ2 = cos θ3 (9) 式
(6) 式 (8) 式 表示 C 、D 和 A 、B 在 一条直线上, 且 C 、D 在 A 、B 之间 。
(7) 式 (9) 式 也表示 C 、D 和 A 、B 在 一条直线上, 且 C 、D 在 A 、B 之间 。
(6) 式 和 (7) 式 等价, (8) 式 和 (9) 式 等价 。
所以, 结论是, 当 A 、B 、C 、D 在 一条直线上, 且 C 、D 在 A 、B 之间 时, 路径 ACDB 最短 。
当然, 这个 结论 是 显而易见 的, 两点之间直线最短 嘛 。
接下来, 看看 曲面 上 的 短程线 。 短程线 就是 曲面 上 2 点 间 距离 最短 的 线(曲线 / 路径) 。 这个课题 在 本文 命名为 题 (4) 。
设有 曲面 P, 曲面函数 是 z = P ( x, y ) , 曲面 上 有 A 、B 两点, 位置确定 。 A 、B 坐标 是 ( Xa, Ya, za ) 、( Xb, Yb, zb ) ,
其中, za = P ( Xa, Ya ) , zb = P ( Xb, Yb ) , Xa, Ya, Xb, Yb 为 常量 。
在 曲面 上 取一些点 : P1, P2, P3 …… Pn , 按 A, P1, P2, P3 …… Pn, B 的 顺序 把 A 、B 和 这些点 连起来, 构成 一条 路径, 称为 APB 。
APB 是 一条 折线, 长度 记为 L 。
L = AP1 + P1P2 + P2P3 + …… + PnB
= 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² + ( z1 - za ) ² ] + 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] + 根号 [ ( x3 - x2 ) ² + ( y3 - y2 ) ² + ( z3 - z2 ) ² ] + …… + 根号 [ ( Xb - xn ) ² + ( Yb - yn ) ² + ( zb - zn ) ² ]
其中, z1 = P ( x1, y1 ), z2 = P ( x2, y2 ), z3 = P ( x3, y3 ) …… zn = P ( xn, yn )
所以, L 是 x1, y1, x2, y2, x3, y3 …… xn, yn 的 函数, 可以记为 L = f ( x1, y1, x2, y2, x3, y3 …… xn, yn ) , 是 一个 多元函数 。
当 n 为 一个 确定 的 自然数 时, 可以来求 最短 的 APB, 即 确定出 P1, P2, P3 …… Pn 的 位置, 使得 APB 最短 。
求 最短 的 APB 就是 求 L 的 极值 , 根据 n 元函数极值定理, 可以 列方程组 :
∂ L / ∂ x1 = 0 4-1 式
∂ L / ∂ y1 = 0 4-2 式
∂ L / ∂ x2 = 0
∂ L / ∂ y2 = 0
∂ L / ∂ x3 = 0
∂ L / ∂ y3 = 0
……
∂ L / ∂ xn = 0
∂ L / ∂ yn = 0
这个 方程组 称为 方程组 (4) 。
化简 4-1 式 :
∂ ( AP1 + P1P2 + P2P3 + …… + PnB ) / ∂ x1 = 0
∂ ( AP1 ) / ∂ x1 + ∂ ( P1P2 ) / ∂ x1 + ∂ ( P2P3 ) / ∂ x1 + …… + ∂ ( PnB ) / ∂ x1 = 0
因为 P2P3, P3P4, P4P5 …… PnB 和 x1 无关, 所以
∂ ( P2P3 ) / ∂ x1 = 0
∂ ( P3P4 ) / ∂ x1 = 0
∂ ( P4P5 ) / ∂ x1 = 0
…… = 0
∂ ( PnB ) / ∂ x1 = 0
于是
∂ ( AP1 ) / ∂ x1 + ∂ ( P1P2 ) / ∂ x1 + 0 + …… + 0 = 0
∂ ( AP1 ) / ∂ x1 + ∂ ( P1P2 ) / ∂ x1 = 0
∂ { 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² + ( z1 - za ) ² ] } / ∂ x1 + ∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] } / ∂ x1 = 0 (10) 式
同理, 4-2 式 可得 :
∂ { 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² + ( z1 - za ) ² ] } / ∂ y1 + ∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] } / ∂ y1 = 0 (11) 式
方程组 (4) 其它 方程 可得到 类似 (10) 式 (11) 式 的 结果, 所以 方程组 (4) 的 化简结果 是 :
∂ { 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² + ( z1 - za ) ² ] } / ∂ x1 + ∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] } / ∂ x1 = 0
∂ { 根号 [ ( x1 - Xa ) ² + ( y1 - Ya ) ² + ( z1 - za ) ² ] } / ∂ y1 + ∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] } / ∂ y1 = 0
……
∂ { 根号 [ ( xn - xm ) ² + ( yn - ym ) ² + ( zn - zm ) ² ] } / ∂ xn + ∂ { 根号 [ ( Xb - xn ) ² + ( Yb - yn ) ² + ( zb - zn ) ² ] } / ∂ xn = 0 , m = n -1
∂ { 根号 [ ( xn - xm ) ² + ( yn - ym ) ² + ( zn - zm ) ² ] } / ∂ yn + ∂ { 根号 [ ( Xb - xn ) ² + ( Yb - yn ) ² + ( zb - zn ) ² ] } / ∂ yn = 0 , m = n -1
这个 方程组 就是 曲面短程线方程组 。 方程组 (4) 有 2n 个 方程, 曲面短程线方程组 也有 2n 个 方程, 两者一一对应 。
曲面短程线方程组 有 2n 个 未知数 : x1, y1, x2, y2, x3, y3 …… xn, yn ,
把 曲面函数 z = P ( x,y ) 代入 曲面短程线方程组, 可以 解出 x1, y1, x2, y2, x3, y3 …… xn, yn , 也就是 得到了 P1, P2, P3 …… Pn 的 位置,
把 A, P1, P2, P3 …… Pn, B 连起来, 得到 折线 APB , APB 是 A 、B 两点间 节点数 为 n 的 折线 中 最短 的 那一条 。 或者说, APB 是 A 、B 两点间 节点数 为 n 的 最短折线 。
这里 组成 折线 的 线段 是 直线线段, 这些 线段 的 端点 在 曲面 上, 但是 线段 不在 曲面 上, 像是一些 架在 曲面 上的 桥梁 。
当 n -> 无穷 时, 折线 APB 就成了 光滑曲线, 就是 短程线, 当然, 光滑曲线 是 在 曲面 上 的 。
曲面短程线方程组 有 2n 个 未知数, 2n 个 方程, 是 一个 多元方程组, 要 怎么解 呢 ? 用 计算机 解 吧, 哈哈 。 大概 应该是用 计算机 数值方法 来 解 。
当 n 为 有限大小 的 自然数 时, 方程 的 解 是 n 个 点 P1, P2, P3 …… Pn , 把 A, P1, P2, P3 …… Pn, B 连起来 就可以得到 近似的 短程线 。
这可以用于 离散绘制, 比如 计算机模拟绘制 。
刚刚也说了, 曲面短程线方程组 得到 的 解 是 一些点 P1, P2, P3 …… Pn , 理论上, 连接 这些 点 的 线段 是 直线线段,
但 模拟绘制 时, 连接 A, P1, P2, P3 …… Pn, B 的 线段 不一定 是 直线线段, 可以 近似 的 选择 曲面 上 的 曲线线段,
比如, 连接 P1, P2 , 可以 选择 P1, P2 之间 在 曲面 上 的 一条 曲线线段, 大概的, 尽量 让 这条 曲线线段 短一点 就行 。
计算机 数值方法 解 n 元方程组, 当 n 很大时, 计算量(时间复杂度) 很大, 即使 用 跨越步进法, 计算量 还是会很大 。 但有一点好处是, 数值方法 解 n 元方程组 可以 使用 并行计算, 就是说 可以 分解 为 多个 小任务 并行计算 。 未来, 大规模并行计算 是 计算 的 基础架构, 也是 一个 主流, 也是 普及 的, 可以用 大规模并行计算 或 网格计算 等 来 解 n 元方程组, 这就 很爽 了, 哈哈 。
以 P1 、P2 、P3 表示 相邻 的 3 个 点, P1 、P2 、P3 的 坐标 为 ( x1, y1, z1 ) 、( x2, y2, z2 ) 、( x3, y3, z3 ) , 则 曲面短程线方程组 可以 写成 通式 :
∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] } / ∂ x2 + ∂ { 根号 [ ( x3 - x2 ) ² + ( y3 - y2 ) ² + ( z3 - z2 ) ² ] } / ∂ x2 = 0 (12) 式
∂ { 根号 [ ( x2 - x1 ) ² + ( y2 - y1 ) ² + ( z2 - z1 ) ² ] } / ∂ y2 + ∂ { 根号 [ ( x3 - x2 ) ² + ( y3 - y2 ) ² + ( z3 - z2 ) ² ] } / ∂ y2 = 0 (13) 式
其中, z1 = P ( x1, y1 ), z2 = P ( x2, y2 ), z3 = P ( x3, y3 ) 。
(12) 式 (13) 式 就是 曲面短程线微元方程组, 这个 方程组 的 意义 是, 在 曲面 P 上, 由 P1 、P2 两个点, 可以决定 P3 。 P1, P2, P3 连成 的 折线 称为 P1P2P3, 在 曲面 上 可以 任意 取 一个 点 Px, 按 P1, Px, P3 的 顺序 把 3 个点 连起来, 得到 的 折线 称为 P1PxP3, 由于 Px 的 位置任意, 所以, P1PxP3 这样 的 折线 有 无数条, P1P2P3 是 这些 折线 中 最短 的 。
也可以说, P1P2P3 是 P1, P3 间 用 2 条 直线线段 连起来 构成 的 折线 中 最短 的 那一条 。
同样, 可以由 P1, P3 决定 P2, 也可以由 P2, P3 决定 P1, 得到 的 P1P2P3 都是 P1PxP3 中 最短 的 。
(12) 式 (13) 式 中 代入 曲面函数 y = P ( x, y ) 求偏导 化简 后, 得到的是 2 个 方程, 这 2 个 方程 中 有 6 个 未知数 x1, y1, x2, y2, x3, y3 ,
已知 x1, y1, x2, y2 可以求 x3, y3 , 这是 由 P1, P2 决定 P3 。
已知 x1, y1, x3, y3 可以求 x2, y2 , 这是 由 P1, P3 决定 P2 。
已知 x2, y2, x3, y3 可以求 x1, y1 , 这是 由 P2, P3 决定 P1 。
但是, 由 (12) 式 (13) 式 对 x2, y2 求偏导 决定了, 把 P1, P2, P3 连成 折线 的 顺序 是 P1, P2, P3 , 这样 连起来 得到的 折线 P1P2P3 才具有 “最短” 的 意义, 也就是 P1, P3 间 通过 2 条 直线线段 构成 的 折线 中 最短 的 那一条 的 意义 。
进一步, 在 曲面 上, 可以 任选 2 个 点 P1, P2, 由 (12) 式 (13) 式 可以 得到 P3, 再由 P2, P3 通过 (12) 式 (13) 式 得到 P4, 再由 P3, P4 得到 P5, …… 一直到 Pn ,
把 P1, P2, P3, P4, P5 …… Pn 连起来 得到 一条 折线, 称为 P1Pn, P1Pn 是 P1, Pn 间 节点数 为 n - 2 的 最短折线 。 这里 的 节点数 是 P1, Pn 间 的 节点数, 不包括 P1, Pn 2 个点, 所以, P1, Pn 间 的 节点数 是 n - 2 。
(12) 式 (13) 式 这种方程 不是 一般意义 上 的 微分方程, 可以称为 微元方程, 具有 离散性质 。 在 一些时候, 微元方程 可能 转化为 微分方程, 比如 上文 的 题 (1) 、题 (2) 、题 (3) 。
看一下 曲面短程线方程组 的 实际应用, 以 球面 为例, 在 曲面短程线方程组 中 代入 球面函数 y = 根号 ( r ² - x ² - y ² ) , 可以得到 球面短程线方程组 。
在 曲面短程线微元方程组 中 代入 球面函数 y = 根号 ( r ² - x ² - y ² ) , 可以得到 球面短程线微元方程组 。
最后, 留一道题, 这题 在 本文 命名为 题 (5) 。
这题 是 最速降线 的 空间版, 在 三维空间 里, 有 A 、B 两点, 建立一个 三维坐标系 xyz, z 轴 是 竖直方向( 和 重力方向 平行) 。
A 和 B 在 竖直方向 上 不在 一个平面 上, 这是 和 二维版 最速降线 的 区别, 二维版 的 最速降线 A 和 B 在 重力方向 上 在 同一个平面 。
A 点 比 B 点 高 , 问 小球 从 A 沿着 怎样 的 曲线 滚动 到 B 所用 的 时间 最短 ? 当然, 这条 曲线 就是 A 、B 间 的 最速降线, 也是 空间 中 的 最速降线 。