牛客网-剑指offer编程题解答。

前言?

牛客网-剑指offer大部分题目的解答，环境为牛客网的在线环境。不会详细解答思路，会在代码中尽量解释主要代码含义。以下按考点划分。

1. 二维数组中的查找

题目描述
在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

public class Solution {
    public boolean Find(int target, int[][] array) {
        // 判断数组是否为null、[]、[[]]
        if ((array == null || array.length == 0) || (array.length == 1 && array[0].length == 0))
            return false;
        int col = array.length - 1;
        int row = 0;
        // 数组从array最左下角开始，值比target大就往上走，值比target小就往右走
        while (col >= 0 && row < array[0].length) {
            if (array[col][row] > target)
                col--;
            else if (array[col][row] < target)
                row++;
            else
                return true;
        }
        // 没找到即返回false
        return false;
    }
}

2. 构建乘积数组

题目描述
给定一个数组A[0,1,…,n-1],请构建一个数组B[0,1,…,n-1],其中B中的元素B[i]=A[0]A[1]…*A[i-1]A[i+1]…*A[n-1]。不能使用除法。

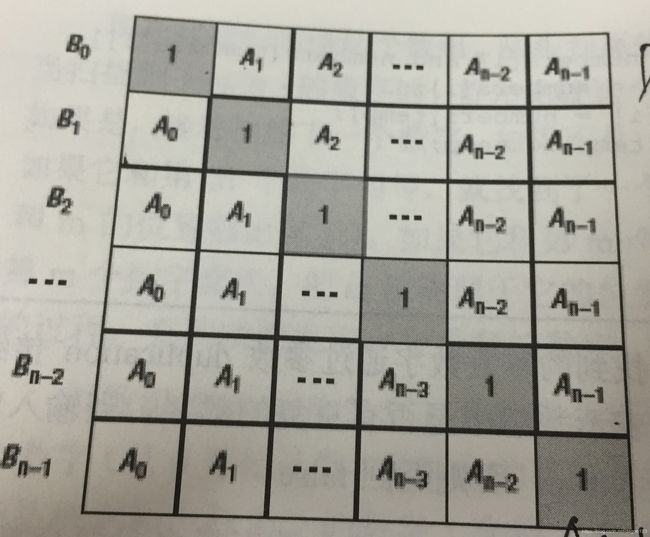
如图所示，所以可以拆成两部分，第一部分计算A[0]A[1]…A[i-1]，第二部分计算A[i+1]…*A[n-1];

import java.util.ArrayList;

public class Solution {
    public int[] multiply(int[] A) {
        if (A.length == 0) {
            return A;
        }
        int[] B = new int[A.length];
        B[0] = 1;
        // 第一部分，计算A[0]*A[1]*...*A[i-1]
        for (int i = 1; i < A.length; i++)
            B[i] = B[i - 1] * A[i - 1];
        int tmp = 1;
        // 第二部分，计算A[i+1]*...*A[n-1]
        for (int i = A.length - 2; i >= 0; i--) {
            tmp *= A[i + 1];
            B[i] *= tmp;
        }
        return B;
    }
}

3. 数组中重复的数字

题目描述
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

解法一：通常解法，利用hashset(其实也可以用hashmap)

import java.util.HashSet;

public class Solution {
    // Parameters:
    // numbers: an array of integers
    // length: the length of array numbers
    // duplication: (Output) the duplicated number in the array number,length of
    // duplication array is 1,so using duplication[0] = ? in implementation;
    // Here duplication like pointor in C/C++, duplication[0] equal *duplication in
    // C/C++
    // 这里要特别注意~返回任意重复的一个，赋值duplication[0]
    // Return value: true if the input is valid, and there are some duplications in
    // the array number
    // otherwise false
    // 方法1
    public boolean duplicate(int numbers[], int length, int[] duplication) {
        if (length < 2 || numbers == null)
            return false;
        HashSet<Integer> result = new HashSet<>();
        for (int i = 0; i < numbers.length; i++) {
            if (!result.add(numbers[i])) {
                duplication[0] = numbers[i];
                return true;
            }
        }
        return false;
    }
}

解法二：不需要利用额外空间，题目里写了数组里数字的范围保证在0~n-1之间，所以可以利用现有数组设置标志，当一个数字被访问过后，可以设置对应位上的数+ n，之后再遇到相同的数时，会发现对应位上的数已经大于等于n了，那么直接返回这个数即可。

public class Solution {
    public boolean duplicate2(int numbers[], int length, int[] duplication) {
        if (length < 2 || numbers == null)
            return false;
        for (int i = 0; i < length; i++) {
            // 取得numbers[i]的值
            int index = numbers[i];
            // 如果大于length，则需要减去length获得numbers[i]的值
            if (index >= length)
                index -= length;
            // 若已经大于length，说明已经有过访问
            if (numbers[index] >= length) {
                duplication[0] = index;
                return true;
            }
            // numbers[i]对应位置上的数字+length
            numbers[index] = numbers[index] + length;
        }
        return false;
    }
}

举个例子,数组{1，2，3，2，3}
当i=0时，index=numbers[i]=1, 小于length，index=1
numbers[index]=2 小于length，说明第一次访问
此时标记访问记录，numbers[index]=2+length; 即numbers[1]=2+length;
当i=1时，index=numbers[i]=2+length，大于ength，需要取得真实值，减去length，index=2
numbers[index]=3 小于length，说明第一次访问
此时标记访问记录，numbers[index]=3+length; 即numbers[2]=3+length;
当i=2时，index=numers[i]=3+length,大于length，需要取得真实值，减去length，index=3
numbers[index]=2 小于length，说明第一次访问
此时标记访问记录，numbers[index]=2+length;即numbers[3]=2+length;
当i=3时，index=numbers[i]=2+length,大于length，需要取得真实值，减去length，index=2
numbers[index]=3+length 大于length，说明第二次访问
此时返回index的值

4. 替换空格

题目描述
请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

public class Solution {
    public String replaceSpace(StringBuffer str) {
        String str1 = str.toString();
        char[] str2 = str1.toCharArray();
        StringBuilder str3 = new StringBuilder();
        for (int i = 0; i < str2.length; i++) {
            if (str2[i] == ' ') {
                str3.append("%20");
            } else {
                str3.append(str2[i]);
            }
        }
        return str3.toString();
    }
}

5. 从尾到头打印链表

题目描述
输入一个链表，按链表值从尾到头的顺序返回一个ArrayList。

import java.util.Stack;
import java.util.ArrayList;

public class Solution {
    
    public ArrayList<Integer> printListFromTailToHead(ListNode listNode) {
        ArrayList<Integer> result = new ArrayList<>();
        Stack<Integer> stack = new Stack<>();
        // 利用栈先进后出的思想
        while (listNode != null) {
            stack.push(listNode.val);
            listNode = listNode.next;
        }
        while (!stack.isEmpty()) {
            result.add(stack.pop());
        }
        return result;
    }
}

6. 重建二叉树

题目描述
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

采用递归的思想，根据前序遍历和中序遍历，先构建根节点，再构建根节点的左右子树。然后将左右子树分别看成独立的一棵树，再构建根节点与左右子树，如此下去。

/**
 * Definition for binary tree
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    public TreeNode reConstructBinaryTree(int[] pre, int[] in) {
        TreeNode root = reConstructBinaryTree(pre, 0, pre.length - 1, in, 0, in.length - 1);
        return root;
    }

    private TreeNode reConstructBinaryTree(int[] pre, int sPre, int ePre, int[] in, int sIn, int eIn) {
        if (sPre > ePre || sIn > eIn)
            return null;
        // 此部分的根节点
        TreeNode root = new TreeNode(pre[sPre]);
        for (int i = sIn; i <= eIn; i++) {
            // 根据中序遍历获取左右子树
            if (in[i] == pre[sPre]) {
                // i-sIn为左右子树的节点个数
                root.left = reConstructBinaryTree(pre, sPre + 1, sPre + i - sIn, in, sIn, i - 1);
                root.right = reConstructBinaryTree(pre, sPre + i - sIn + 1, ePre, in, i + 1, eIn);
            }
        }
        return root;
    }
}

7. 用两个栈实现队列

题目描述
用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

import java.util.Stack;

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();

    public void push(int node) {
        stack1.push(node);

    }

    // 如果stack2为空，则需从stack1中读取
    public int pop() {
        if (stack2.isEmpty()) {
            while (!stack1.isEmpty()) {
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

8. 旋转数组的最小数字

题目描述
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

最简单的方法，因为是非减排序数组，直接遍历。

import java.util.ArrayList;
public class Solution {
    // 直接遍历法
    public int minNumberInRotateArray(int[] array) {
        if (array.length == 0)
            return 0;
        for (int i = 0; i < array.length - 1; i++) {
            if (array[i] > array[i + 1])
                return array[i + 1];
        }
        return array[0];
    }
}

稍微优化一下，采用二分查找法

需要考虑三种情况：
(1)array[mid] > array[high]:
出现这种情况的array类似[3,4,5,6,0,1,2]，此时最小数字一定在mid的右边。
low = mid + 1
(2)array[mid] == array[high]:
出现这种情况的array类似 [1,0,1,1,1] 或者[1,1,1,0,1]，此时最小数字不好判断在mid左边
还是右边,这时只好一个一个试 ，
high = high - 1
(3)array[mid] < array[high]:
出现这种情况的array类似[2,2,3,4,5,6,6],此时最小数字一定就是array[mid]或者在mid的左
边。因为右边必然都是递增的。
high = mid
注意这里有个坑：如果待查询的范围最后只剩两个数，那么mid 一定会指向下标靠前的数字
比如 array = [1,0,1]
array[low] = 1 ;array[mid] =0 ; array[high] = 1 ;
如果high = mid - 1，就会产生错误，return array[low] 此时的low=0;
但情形(1)中low = mid + 1就不会错误

import java.util.ArrayList;

public class Solution {
    // 二分查找法
    public int minNumberInRotateArray2(int[] array) {
        if (array.length == 0)
            return 0;
        int low = 0;
        int high = array.length - 1;
        while (low < high) {
            int mid = (low + high) >>> 1;// 防止溢出
            if (array[mid] > array[high]) {
                low = mid + 1;
            } else if (array[mid] == array[high]) {
                high = high - 1;
            } else {
                high = mid;
            }
        }
        return array[low];
    }
}

9. 斐波那契数列

题目描述
大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。
n<=39

递归

public class Solution {
    // 递归
    public int Fibonacci(int n) {
        if (n == 0)
            return 0;
        if (n == 1 || n == 2)
            return 1;
        else
            return Fibonacci(n - 1) + Fibonacci(n - 2);
    }
}

非递归，打表的方式

public class Solution {
    // 非递归 打表
    public int Fibonacci2(int n) {
        int[] result = new int[40];
        result[1] = 1;
        result[2] = 1;
        for (int i = 3; i <= n; i++)
            result[i] = result[i - 2] + result[i - 1];
        return result[n];
    }
}

10. 跳台阶

题目描述
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

这种题目是斐波那契数列的变形题目。跳第n层台阶可以看作 第n-1层台阶的方法次数（最后一步条1层台阶）+第n-2层台阶的方法次数（最后一步跳2层台阶）

递归

public class Solution {
    // 递归
    public int JumpFloor(int target) {
        if (target < 3)
            return target;
        else
            return JumpFloor(target - 1) + JumpFloor(target - 2);
    }
}

非递归，打表的方式

public class Solution {
    // 非递归
    public int JumpFloor2(int target) {
        if (target < 3)
            return target;
        int[] result = new int[target + 1];
        result[1] = 1;
        result[2] = 2;
        for (int i = 3; i <= target; i++) {
            result[i] = result[i - 1] + result[i - 2];
        }
        return result[target];
    }
}

11. 变态跳台阶

题目描述
一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

这种题目是斐波那契数列的变形题目。跳第n层台阶可以看作 = 第n-1层台阶的方法次数 + 第n-2层台阶的方法次数……第1层台阶的方法次数 + 一步跳到第n层台阶。

递归

public class Solution {
    // 递归
    public int JumpFloor(int target) {
        if (target < 3)
            return target;
        else {
            int result = 0;
            for (int i = 1; i < target; i++) {
                result += JumpFloorII(i);
            }
            return result + 1;
        }
    }
}

非递归

public class Solution {
    // 非递归
    public int JumpFloor2(int target) {
        if (target < 3)
            return target;
        int[] result = new int[target + 1];
        result[1] = 1;
        result[2] = 2;
        for (int i = 3; i <= target; i++) {
            for (int j = 1; j < i; j++) {
                result[i] += result[j];
            }
            result[i] += 1;
        }
        return result[target];
    }
}

12.矩形覆盖

题目描述
我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

依旧是斐波那契数列
2n的大矩形，和n个21的小矩形
其中target*2为大矩阵的大小
有以下几种情形：
1、target = 0 大矩形为<= 2 * 0,直接return 0；
2、target = 1大矩形为2 * 1，只有一种摆放方法，return 1；
3、target = 2 大矩形为2 * 2，有两种摆放方法，return 2；
4、target = n 分为两步考虑：
第一次摆放一块 2 * 1 的小矩阵，则摆放方法总共为f(target - 1)

✔
✔

第一次摆放一块 1 * 2 的小矩阵，则摆放方法总共为f(target - 2)
因为，摆放了一块12的小矩阵（用✔ ✔ 表示），对应下方的12（用 ✖ ✖表示）摆放方法就确定了，所以为f(targte-2)

✔	✔
✖	✖

递归

public class Solution {
    // 递归
    public int RectCover(int target) {
        if (target < 3)
            return target;
        else
            return RectCover(target - 2) + RectCover(target - 1);
    }
}

非递归，打表的方式

public class Solution {
    // 非递归
    public int RectCover2(int target) {
        if (target < 3)
            return target;
        int[] result = new int[target + 1];
        result[1] = 1;
        result[2] = 2;
        for (int i = 3; i <= target; i++) {
            result[i] = result[i - 1] + result[i - 2];
        }
        return result[target];
    }
}

13. 二进制中1的个数

题目描述
输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

思想：用1（1自身左移运算，其实后来就不是1了）和n的每位进行位与，来判断1的个数

public class Solution {
    // 思想：用1（1自身左移运算，其实后来就不是1了）和n的每位进行位与，来判断1的个数
    public int NumberOf1(int n) {
        int result = 0;
        int index = 1;
        while (index != 0) {
            if ((n & index) != 0) {
                result++;
            }
            index = index << 1;
        }
        return result;
    }
}

最优解：

public class Solution {
    // 最优解
    public int NumberOf12(int n) {
        int count = 0;
        while (n != 0) {
            count++;
            n = (n - 1) & n;
        }
        return count;
    }
}

分析：如果一个整数不为0，那么这个整数至少有一位是1。如果我们把这个整数减1，那么原来处在整数最右边的1就会变为0，原来在1后面的所有的0都会变成1(如果最右边的1后面还有0的话)。其余所有位将不会受到影响。
举个例子：一个二进制数1100，从右边数起第三位是处于最右边的一个1。减去1后，第三位变成0，它后面的两位0变成了1，而前面的1保持不变，因此得到的结果是1011.我们发现减1的结果是把最右边的一个1开始的所有位都取反了。这个时候如果我们再把原来的整数和减去1之后的结果做与运算，从原来整数最右边一个1那一位开始所有位都会变成0。如1100&1011=1000.也就是说，把一个整数减去1，再和原整数做与运算，会把该整数最右边一个1变成0.那么一个整数的二进制有多少个1，就可以进行多少次这样的操作。

14. 数值的整数次方

题目描述
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。

分三种情况：
1、指数 > 0
2、指数 = 0
3、指数 < 0 (第一种情况的倒数)

public class Solution {
    public double Power(double base, int exponent) {
        double result = 1.0;

        if (exponent > 0) {
            for (int i = 1; i <= exponent; ++i) {
                result *= base;
            }
        } else if (exponent == 0) {
            return result;
        } else {
            if (base == 0)
                throw new RuntimeException("分母不能为零");
            for (int i = 1; i <= -exponent; ++i) {
                result *= base;
            }
            result = 1 / result;
        }
        return result;
    }
}

15. 调整数组顺序使奇数位于偶数前面

题目描述
输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

找到奇数时，将奇数放到最前面的偶数位置，并且将所有偶数后移。

public class Solution {
    public void reOrderArray(int[] array) {
        for (int i = 0; i < array.length; i++) {
            if (array[i] % 2 != 0) {
                for (int j = 0; j < i; j++) {
                    if (array[j] % 2 == 0) {
                        array[i] ^= array[j];
                        array[j] ^= array[i];
                        array[i] ^= array[j];
                    }
                }
            }
        }
    }
}

16. 链表中倒数第K个节点

题目描述
输入一个链表，输出该链表中倒数第k个结点。

当p抵达链表末端（即null时），p与q之间的节点数为k-1个，所以q当前的节点即为倒数第k个节点。
如果p抵达链表末端时，计数器还小于k，说明k大于链表长度，返回null。

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode FindKthToTail(ListNode head, int k) {
        ListNode p, q;
        p = q = head;
        int i = 0;
        for (; p != null; i++) {
            if (i >= k)
                q = q.next;
            p = p.next;
        }
        return i < k ? null : q;
    }
}

17. 反转链表

题目描述
输入一个链表，反转链表后，输出新链表的表头。

"->“表示next，”-"表示当前值

1、 1->2->3->4->5
pre-null cur-1 tmp-2

2、 2->3->4->5 1->null
pre-null cur-1 tmp-2

3、 2->3->4->5 1->null
pre-1 cur-2 tmp-3

4、 3->4->5 2->1->null
pre-2 cur-2 tmp-3

5、 3->4->5 2->1->null
pre-2 cur-3 tmp-4
……

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode ReverseList(ListNode head) {
        if (head == null) {
            return null;
        }
        ListNode cur, pre;
        cur = head;
        pre = null;
        while (cur.next != null) {
            ListNode tmp = cur.next;
            cur.next = pre;
            pre = cur;
            cur = tmp;
        }
        cur.next = pre;
        return cur;
    }
}

18. 合并两个排序的链表

题目描述
输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

/*
public class ListNode {
    int val;
    ListNode next = null;

    ListNode(int val) {
        this.val = val;
    }
}*/
public class Solution {
    public ListNode Merge(ListNode list1, ListNode list2) {
        if (list1 == null) {
            return list2;
        } else if (list2 == null) {
            return list1;
        }
        ListNode mergeNode = null;
        if (list1.val < list2.val) {
            mergeNode = list1;
            mergeNode.next = Merge(list1.next, list2);
        } else {
            mergeNode = list2;
            mergeNode.next = Merge(list1, list2.next);
        }
        return mergeNode;
    }
}