Machine Learning 05 - Model Evaluation and Analysis

正在学习Stanford吴恩达的机器学习课程，常做笔记，以便复习巩固。
鄙人才疏学浅，如有错漏与想法，还请多包涵，指点迷津。

5.1 Evaluation

5.1.1 Hypothesis evaluation

a. Evaluation method
Given a dataset of training examples. we can split up it into two parts.Typically, we can divide the dataset :

Remark :

• Both of the two parts must have the same data distribution.
• The sample partitioning method should be randomly choosed, thus we should try the evaluation process many times and take an average.
• Different cases have different size of training set and test set.

b. Performance measurement
For linear regression :

Jtest(Θ)=12mtest∑i=1mtest(hΘ(x(i)test)−y(i)test)2 J t e s t ( Θ ) = 1 2 m t e s t ∑ i = 1 m t e s t ( h Θ ( x t e s t ( i ) ) − y t e s t ( i ) ) 2

For classification :

err(hΘ(x),y)={10if hΘ(x)≥0.5 and y=0 or hΘ(x)≤0.5 and y=1otherwise e r r ( h Θ ( x ) , y ) = { 1 0 if  h Θ ( x ) ≥ 0.5  and  y = 0  or  h Θ ( x ) ≤ 0.5  and  y = 1 otherwise

Test Error=1mtext∑i=1mtesterr(hΘ(x(i)test),y(i)test) Test Error = 1 m t e x t ∑ i = 1 m t e s t e r r ( h Θ ( x t e s t ( i ) ) , y t e s t ( i ) )

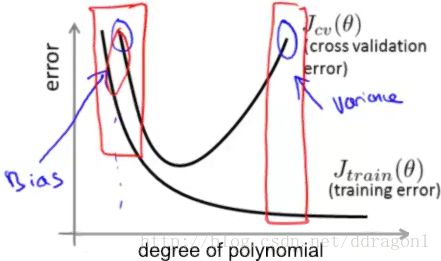
c. Example 1 : model selection

Let us talk about the selection of polynomial degree.

We can test each degree of polynomial and look at the error. It is suggested that we should divide the dataset into three parts, usually is :

In general, we can evaluate our hypothesis using the following method :

• 1.Optimize the Θ Θ using the training set for each polynomial degree.
• 2.Find the polynomial degree with the least error using the cross validation set.
• 3.Esitimate the generalization error using the test set with Jtest(Θ(d)) J t e s t ( Θ ( d ) ) .

5.1.2 Bias and variance

a. Bias and variance

Given a model, we have two concepts:

Bias : underfit, both train error and the cross validation error is high, also JCV(Θ)≈Jtrain(Θ) J C V ( Θ ) ≈ J t r a i n ( Θ ) .

Variance : overfit, the cross validation error is high but the train error is very low, also Jtrain(Θ)≪JCV(Θ) J t r a i n ( Θ ) ≪ J C V ( Θ ) .

b. Relations of regularization

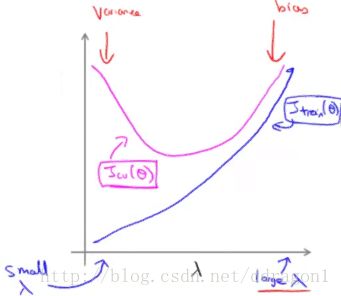
Consider λ λ in regularization :

when λ λ is very large, our fit becomes more rigid.

when λ λ is very samll, we tend to over overfit the data.

c. Example 2 : regularization selection

We can find the best lambda using the methods below :

• 1.Learn some Θ Θ using a list of lambdas.
• 2.Compute the cross validation error using the Θ Θ , and choose the best combo that produces the lowest error on the cross validation set.
• 3.Using the best combo of Θ Θ and λ λ to compute the test error.

5.1.3 Learning curves

a. Relations of dataset

We can easily know that :

when the dataset is very small, we can get 0 0 train errors while the cross validation error is large. As the dataset get larger, the train errors increase, and the cross validation decrease.

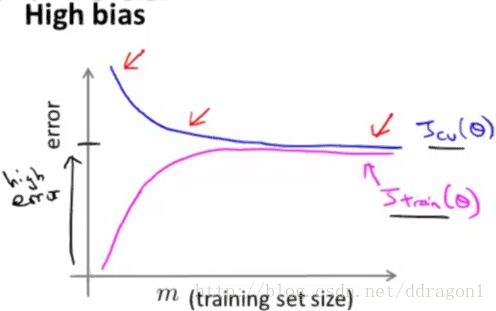
In the high bias problem :

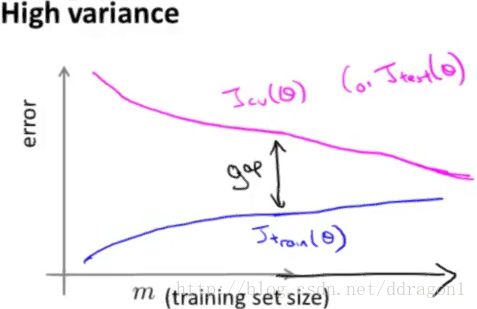
In the high variance problem :

b. Example 3 : whether to add data

When experiencing high bias :

• Low training set size causes low Jtrain(Θ) J t r a i n ( Θ ) and high JCV(Θ) J C V ( Θ ) .
• High training set size casuses both high Jtrain(Θ) J t r a i n ( Θ ) and high JCV(Θ) J C V ( Θ ) .

Getting more training data will not help much.

When experiencing high variance :

• Low training set size casuses low Jtrain(Θ) J t r a i n ( Θ ) and high JCV(Θ) J C V ( Θ ) .
• High training set size result in increasing Jtrain(Θ) J t r a i n ( Θ ) and decreasing JCV(Θ) J C V ( Θ ) , but still Jtrain(Θ)<JCV(Θ) J t r a i n ( Θ ) < J C V ( Θ ) significantly.

Getting more training data is likely to help.

5.1.4 Summary

Our decision process can be broken down as follows:

• Getting more training examples: Fixes high variance
• Trying smaller sets of features: Fixes high variance
• Adding features: Fixes high bias
• Adding polynomial features: Fixes high bias
• Decreasing λ: Fixes high bias
• Increasing λ: Fixes high variance.

Addition ：

A neural network with fewer parameters is prone to underfitting. It is also computationally cheaper.

A neural network with more parameters is prone to overfitting. It is also computationally expensive.

The knowledge above (such as 5.1.1) is also useful to neural network.

5.2 System Design

5.2.1 Error analysis

We have konwn how to evaluate a model. Next we will talk about the whole process when facing a machine learning problem.

Error analysis : after model training and evaluation, in order to choose which method is best or get some ideas, we will manually spot the errors in cross validation set, calculating the algorithm’s performance.

5.2.2 Examples & Experience

(1) Skewed Data

Skewed data : the error metric of the algorithm can be very low, in which case a simple algorithm (like y=0 y = 0 ) is better.

Solution : use better metric

Precision :

P=TPTP+FP P = T P T P + F P

Recall :

R=TPTP+FN R = T P T P + F N

Trade-off between T and R
In order to compare different algorithm with P-R metric, we can use

F-score

F=2PRP+R F = 2 P R P + R

(2) Large Dataset

Training on a lot of data is likely to give good performance when two of the following conditions hold true :

• Our learning algorithm is able to represent fairly complex functions.
• if we have some way to be confident that x x contains sufficient information to predict y y accurately

5.2.3 Summary

The recommanded approach to solve machine learning problems is :

• Start with a simple algorithm, implement it quickly and test validation error. (model training)
• Plot learning curves to evluate the model and decide if more data, more features etc. are likely to help. (model evaluation)
• Manually examine the errors on examples in the cross validation set and try to spot a trend where most of errors were made. (error analysis)

Tricks : Numerical Metric

Get error result as a single, numerical value can help assess algorithm’s performance.

More content abour numerical metric will be talk next time.