数字图像处理——第四章(频率域滤波)
文章目录
- 一、傅里叶变换基础知识
- 1.1 复数
- 1.2 傅里叶级数
- 1.3 一维连续函数傅里叶变换对
- 1.4 一维离散傅里叶变换对(DFT)
- 1.5 二维连续傅里叶变换对
- 1.6 二维离散傅里叶变换对
- 1.7 卷积定理
- 1.8 二维卷积定理
- 1.9 二维离散傅里叶变换的性质
- 周期性
- 傅里叶谱和相角
- 对称性
- 均值
- 二、快速傅里叶变换
- 2.1 fft2函数
- 2.2 fftshift函数
- 2.3 ifft2函数
- 三、频率域滤波基础
- 3.1 傅里叶变换的频率分量和图像空间特征之间的联系
- 3.2 频率域滤波步骤
- 四、使用频率域滤波器平滑图像
- 4.1 理想低通滤波器(ILPF)
- 4.1.1 构造滤镜:
- 4.1.2 应用
- 4.2 布特沃斯低通滤波器(BLPF)
- 4.2.1构造滤镜
- 4.2.2 应用
- 4.3 高斯低通滤波器(GLPF)
- 4.3.1 生成滤镜
- 4.3.2 应用
- 五、使用频率域滤波器锐化图像
- 5.1 理想高通滤波器(IHPF)
- 5.2 布特沃斯高通滤波器(BHPF)
- 5.3 高斯高通滤波器(GHPF)
- 5.3.1 生成滤镜
- 5.3.2 应用
- 5.4 拉普拉斯滤波器
- 5.4.1 生成滤镜
- 5.4.2 实现
- 5.5 锐化滤波器
- 六、选择滤波器
- 6.1 带阻和带通滤波器
- 6.2 陷波滤波器
本章主要介绍傅里叶变换的基本原理,并在基本的图像滤波中使用傅里叶变换。
很多情况下,频率域滤波和空间域滤波可视为对于同一图像增强问题的殊途同归的两种解决方式。一些在空间域困难的增强任务,在频率域中变得非常普通。
傅里叶级数:任何周期函数可表示为不同频域的正弦和/或余弦之和的形式,每个正弦项和/或余弦项乘以不同的系数,这个和的形式称为傅里叶级数。
傅里叶变换:非周期函数(但该曲线下的面积是有限的)也可以用正弦和/或余弦乘以加权函数的积分表示。
傅里叶级数或傅里叶变换表示的函数特征完全可以通过傅里叶反变换来重建,且不丢失任何信息。故傅里叶变换可以使我们工作在频率域,而在转换回空间域时不丢失任何信息。
一、傅里叶变换基础知识
1.1 复数
![]()
R和I是实数,j是一个等于-1的平方根的虚数。R表示实部,I表示虚部。
复数C的共轭复数(实部相等,虚部相反):
![]()
欧拉公式
![]()
1.2 傅里叶级数
具有周期T的连续变量t的周期函数f(t)可描述为乘以适当系数的正弦和余弦之和,这个和即为傅里叶级数,形式如下:

其中

1.3 一维连续函数傅里叶变换对
f(t)为非周期函数。
正变换
![]()
f(x)表示原函数,F(u)表示变换之后的函数。u为频率域变量。
反变换
![]()
1.4 一维离散傅里叶变换对(DFT)
一维函数f(x) (其中x = 0,1,2,……,M-1)。

1.5 二维连续傅里叶变换对
1.6 二维离散傅里叶变换对

f(x,y)是大小为M x N的数字图像。(x,y)表示空间域坐标,(u,v)表示频率域坐标。
同样,1/MN的位置并不重要,也可放在正变换前面。正反变换前的系数乘积为1/MN即可。
1.7 卷积定理
在频率域中,我们感兴趣的是具有连续变量t的两个连续函数的卷积。
空间域中两个函数的卷积的傅里叶变换,等于两个函数的傅里叶变换在频率域的乘积。反之,有频率域两个变换的乘积,可通过计算傅里叶反变换得到空间域的卷积。
空间域中两个函数的乘积的傅里叶变换,等于两个函数的傅里叶变换在频率域的卷积;反之,有频率域两个变换的卷积,可以通过计算傅里叶反变换得到空间域的乘积。

卷积的离散等价表示:

x = 0,1,2……M-1
星号算子表示卷积。t所在的域为空间域,u所在的域为频率域。
卷积定理是频率域滤波的基础。
1.8 二维卷积定理

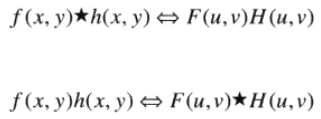
第一个公式:
两个空间函数的卷积可以通过计算两个傅立叶变换函数的乘积的逆变换得到;相反,两个空间函数卷积的傅立叶变换恰好等于两个函数的傅立叶变换的乘积
第二个公式同理。
1.9 二维离散傅里叶变换的性质
周期性
二维傅里叶变换及其反变换在u方向和v方向是无限周期的。

其中k1和k2是整数。
傅里叶谱和相角
二维DFT通常是复函数,可用极坐标形式表示:
![]()
傅里叶谱(频谱)
![]()
频谱是图像增强中最关心的主要对象,频域下每一点(u,v)的|F(u,v)|可用来表示该频率的正弦(余弦)平面波在叠加中所占的比例。频谱直接反应频率信息,是频率域滤波的一个主要依据。
相位角

相位角表面上看并不那么直观,但它隐含着实部与虚部之间的某种比例关系,因此与图像结构息息相关。
功率谱(谱密度)
![]()
R和I分别为F(u,v)的实部和虚部。
对称性
实函数f(x,y)的傅里叶变换是共轭对称的。
![]()
虚函数f(x,y)的傅里叶变换是共轭反对称的。
![]()
傅里叶谱关于原点偶对称。
![]()
相位角关于原点奇对称。
![]()
均值
二维傅里叶正变换如下

若将系数1/MN放在正变换前,则:

故:

又因为

所以,F(0,0),即原点处的傅里叶变换值为原图像f(x,y)的平均灰度级。
小结
DFT定义及相应表达式
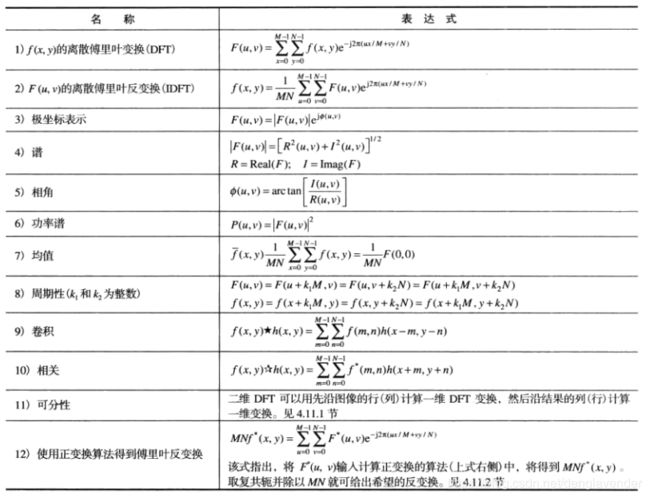
DFT对小结

其中第12项和第13项中的闭合表达式仅对连续变量有效。通过对闭合形式的连续表达式取样后,它们也可用于离散变量。
二、快速傅里叶变换
DFT的直接实现效率很低。一种计算离散傅里叶变换的高效算法应运而生,即为快速傅里叶变换(FFT)。
matlab中提供了fft2和ifft2函数分别计算二维傅里叶变换和反变换。它们都经过了优化,运算速度非常快;使用fftshift函数,将傅里叶频谱图中的零频点移动到频谱图的中心位置。
2.1 fft2函数
用于执行二维快速傅里叶操作,可直接用于数字图像处理。调用语法为:
Y = fft2(X)
Y = fft2(X,m,n)
其中,X为输入图像;
m和n分别用于将X的第一和第二维规整到指定的长度。当m和n均为2的整数次幂时,算法的执行速度要比m和n均为素数时更快;
Y是计算得到的傅里叶变换,是一个复数矩阵。
计算abs(Y)可得到频谱,计算angle(Y)可得到相位角
I1 = imread('C:\Users\win\Desktop\fence-climbing.jpg');
I2 = imread('C:\Users\win\Desktop\city-street.jpg');
img1 = rgb2gray(I1);
img2 = rgb2gray(I2);
F1 = fft2(img1); % 对图像进行快速傅里叶变换
temp = fftshift(F1); % 将零点移到中心
final1 = log(1 + abs(temp)); % 对频率进行对数变换,以压缩动态范围
F2 = fft2(img2);
temp = fftshift(F2);
final2 = log(1 + abs(temp));
figure();
subplot(2,2,1);
imshow(img1);
title('fence-climbing');
subplot(2,2,2);
imshow(img2);
title('city-street');
subplot(2,2,3);
imshow(final1,[]);
title('fence-climbing FFT');
subplot(2,2,4);
imshow(final2,[]);
title('city-street FFT');
- 原图与频谱图相比较,低频对应图像中变化较缓慢的像素区,如图像的平滑部分;高频对应灰度变化较剧烈的像素区,如边缘和噪声等尖锐部分。
- 图city-street较为平滑,在其傅里叶频谱图中,低频部分对应的幅值比较高;而图fence-climbing中,人及围栏杆的灰度变化比较剧烈,对应的频谱中高频分量较强(但整体还是低频区域更多,大部分的黑色区还是属于低频)。故,图像经过快速傅里叶变换后,频谱可以反映原图像中的灰度变化情况。
2.2 fftshift函数
在fft2函数输出的频谱分析数据中,是按照原始计算所得的顺序来排列频谱的,而没有以零频为中心来排列,因此造成了零频在频谱矩阵的角上,显示幅度谱图像时表现为4个亮度较高的角(零频处的幅值较高)。

fftshift函数利用了频谱的周期性特点,将输出图像的一半平移到另一端,从而使零频被移动到图像的中间。调用语法为:
Y = fftshift(X)
Y = fftshift(X,dim)
其中,X为要平移的频率谱;
dim指出了在多维数组的哪个维度上执行平移操作;
Y为经过平移后的结果。
对于二维图像矩阵,fftshift函数的评议过程如下:
输出矩阵被分为了4个部分,其中1、3两部分对换,2、4两部分对换。这样,原来在角上的零频率点(原点)位置就移动到了图像的中央位置。参数dim则可指定在多维数组的哪个维度上执行对换操作。

2.3 ifft2函数
用于对图像(矩阵)执行逆傅里叶变换。输出矩阵的大小与输入矩阵的大小相同。调用形式为:
Y = ifft2(X)
Y = ifft2(X,m,n)
其中,X为要计算反变换的频率谱;
m、n的意义与fft2中相同;
Y是反变换后得到的原始图像。
==注:==在只想ifft2函数前,如果曾经使用fftshift函数对频域图像进行过原点平移,则还需要使用ifftshift函数将原点平移回原位置。
小示例:交换两幅图像的相位谱
%交换两幅图像的相位角
A = imread('C:\Users\win\Desktop\girl.jpg');
B = imread('C:\Users\win\Desktop\dog.jpg');
% A = rgb2gray(f1);
% B = rgb2gray(f2);
%对两幅图像进行傅里叶变换
YA = fft2(A);
YB = fft2(B);
%分别求两幅图像的频谱和相位角
YA1 = abs(YA);
YA2 = angle(YA);
YB1 = abs(YB);
YB2 = angle(YB);
%交换相位角并重建复数矩阵
YAR = YA1.*cos(YB2) + YA1.*sin(YB2).*i;
YBR = YB1.*cos(YA2) + YB1.*sin(YA2).*i;
%傅里叶反变换
XA = abs(ifft2(YAR));
XB = abs(ifft2(YBR));
%显示图像
figure();
subplot(2,2,1);
imshow(A);
title('girl');
subplot(2,2,2);
imshow(B)
title('dog');
subplot(2,2,3);
imshow(XA/256); % 将图像矩阵转换到0-1之间,用来显示彩色图像
% imshow(XA,[]); % 加‘[]’可以自动调整数据的范围以便于显示,用来显示黑白图像。使用时先将读入的图像转换成灰度图,如5、6行
title('girl的频谱+dog的相位角');
subplot(2,2,4);
imshow(XB/256);
% imshow(XB,[]);
title('dog的频谱+girl的相位角');
具体可参见imread()和imshow()
- 两幅图经过相位交换后,图像的内容与相位角所对应的图像一致,表明相位角决定图像的轮廓结构;
- 图像的明暗、灰度变化趋势等则取决于频谱谱,即频谱反映了图像整体上各个方向的频率分量的相对强度。
三、频率域滤波基础
3.1 傅里叶变换的频率分量和图像空间特征之间的联系
- 频率成分(u = v = 0)对应图像的平均灰度级。
- 当从变换的原点移开时,低频对应着图像的慢变化分量,如图像的平滑部分。
- 进一步离开原点时,较高的频率对应图像中变化越来越快的灰度级,如边缘或噪声等尖锐部分。
3.2 频率域滤波步骤

1、给定一幅大小为MxN的输入图像f(x,y),选择填充参数P=2M.Q=2N;
2、对f(x,y)添加必要数量的0,形成大小为PXQ的填充图像 fp(x,y);
3、用(−1)x+y乘以fp(x,y),移到其变换中心;
4、计算上图的DFT,得到F(u,v);
5、生成一个实的,对称的滤波函数H(u,v),其大小为PXQ,中心在(P/2,Q/2)处。用阵列相乘得到乘积G(u,v)=H(u,v)F(u,v);即G(i,k)=H(i,k)F(i,k);
6、得到处理后的图像:
![]()
其中,为忽略由于计算不准确导致的寄生复成分,选择实部,下标p指出我们处理的是填充后的图像。
7、 gp(x,y)的左上象限提取MxN区域,得到最终处理结果 g(x,y)
H(u,v)称为滤波器。它在滤波中抑制或除去了频谱中的某些分量,而保留其他的一些频率不受影响,从而达到滤波的目的。类似于日常生活中的筛子,它可以严格按照尺寸使一些物体通过而同时阻止其他物体。
四、使用频率域滤波器平滑图像
低频通过,高频衰减。处理后的图像少尖锐的细节部分而突出平滑过渡的部分。
一幅图像中的边缘和其他急剧灰度变换(如噪声)主要影响其傅里叶变换的高频内容。在频率域平滑可通过衰减高频来达到,即使用低通滤波。
频域滤波器需结合频域滤镜(ff)一起来实现具体的频域滤波功能。
频域滤波函数imfreqfilt(),具体形式如下:
function out=imfreqfilt(I,ff)
imfreqfilt函数:对灰度图像进行频域滤波
imfreqfilt.m
function out=imfreqfilt(I,ff)
% imfreqfilt函数 对灰度图像进行频率滤波
% 参数 I 输入原图像(空间域图像)
% 参数 ff 频域滤镜(大小与原图像相等)
% 返回值 out 滤波后的图像(空间域图像)
%若是RGB,需转换为Gray
if(ndims(I)==3) && (size(I,3)==3) %RGB图像 size(I,3)表示I的第三维分量大小,ndims(I)代表I的维数
I=rgb2gray(I);
end
%检查输入
if( size(I) ~= size(ff) ) % ‘~=’不等于号
msg1=sprintf('%s:滤镜与原图像不等大,请检查输入',mfilename); % mfilename: File name of currently running code
msg2=sprintf('%s:滤镜操作已经取消',mfilename);
eid=sprintf('Image:%s: ImgSizeNotEqual',mfilename);
error(eid,'%s %s',msg1,msg2);
end
%快速FFT
I1=fft2(double(I));
I1=fftshift(I1); % 将原点移动到频率中心
%应用滤镜及反变换
G=I1.*ff; % 对应元素相乘实现滤波。 频域相乘 I(u,v)H(u,v)
G=ifftshift(G); % 将原点从频率中心移回原位
out=ifft2(G); % IFFT得空间域函数
%求幅度
out=abs(out);
%归一化以便显示
out=out/max(out(:));
4.1 理想低通滤波器(ILPF)
在以原点为圆心,以D0为半径的圆内,无衰减地通过所有频率,而在该圆外“阻断”所有频率的二维低通滤波,称为理想低通滤波器。由下述函数确定:

D0是一个正常数,D(u,v)是频率域中,点(u,v)与频率矩形中心(0,0)的距离:

P和Q是填充后的尺寸
理想:在半径为D0的圆内,所有频率无衰减的通过,圆外的所有频率则完全被衰减(滤除)。
理想低通滤波器关于原点径向对称,故其可由一个径向横截面定义,将横截面旋转360度则可得到二维滤波器。
D0为截止频率。
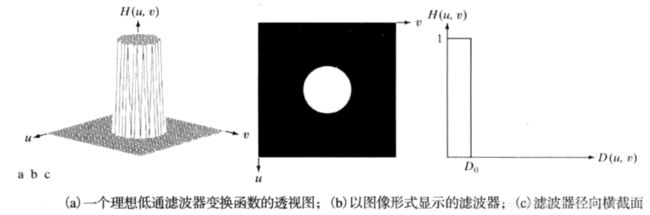
半径D0越大,通过的高频越多,图像模糊度越小,反之亦反。
理想低通滤波器的频率特性在截止频率处十分陡峭,无法用硬件实现,即其称之为理想的原因。
振铃现象是理想滤波器的一种特性。
下图为一幅测试图像即其傅里叶谱。由于填充,该谱的大小为图像大小的两倍,但它是以一半大小来显示的,故页面是匹配的。谱上重叠的圆的半径分别为10,30,60,160和460像素。这些圆包含的图像功率分别为87.0%,93.1%,95.7%,97.8%和99.2%。谱迅速衰落,功率主要集中在圆心附近。

4.1.1 构造滤镜:
理想低通滤镜:imidealflpf()
ff=imidealflpf(I,freq)
功能:构建理想的频域低通滤波器(即滤镜)
imidealflpf.m
function ff=imidealflpf(I,freq)
% imidealflpf函数 构造理想的频域低通滤波器
% I参数 输入的灰度图像
% freq参数 低通滤波器的截止频率
% 返回值 ff 与I等大的频域滤镜
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
if (sqrt (((i-M/2)^2+ (j-N/2)^2 ))>freq)
ff(i,j)=0; %高于截止频率 设为0
end
end
end
4.1.2 应用
idel_LPF.m
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
%生成滤镜 截止频率为20
ff = imidealflpf(img,20);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为40
ff = imidealflpf(img,40);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80
ff = imidealflpf(img,80);
out2 = imfreqfilt(img,ff);
figure(1);
subplot(1,4,1);
imshow(img);
title('原图');
subplot(1,4,2);
imshow(out);
title('截止频域为20');
subplot(1,4,3);
imshow(out1);
title('截止频率为40');
subplot(1,4,4);
imshow(out2);
title('截止频率为80');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
figure(2)
subplot(1,4,1);
imshow(f,[]);
title('原图对应的频谱');
subplot(1,4,2);
imshow(f1,[]);
title('freq = 20 的图像对应的频谱');
subplot(1,4,3);
imshow(f2,[]);
title('freq = 40 的图像对应的频谱');
subplot(1,4,4);
imshow(f3,[]);
title('freq = 80 的图像对应的频谱');
实验结果:


小结:当截止频率非常低时,只有非常靠近原点的低频才能通过滤波器,得到的图像较模糊;截止频率越大,通过的频率越多,得到的图像越清晰。理想低通滤波器并不能很好的兼顾滤除噪声与保留细节两个方面。
4.2 布特沃斯低通滤波器(BLPF)
截止频率位于距原点D0处的n阶布特沃斯低通滤波器的传递函数定义为:



D0越大,通过的高频越多,清晰度越高。
n越大,通过的低频越小,模糊度越高。
经过BLPF处理(n = 2时)的图像中没有可见的振铃现象,归因于该滤波器在低频和高频之间的平滑过渡。
空间域的一阶布特沃斯滤波器没有振铃现象。在二阶滤波器中,振铃现象通常很难察觉,但更高阶数的滤波器中振铃现象会很明显。故,二阶BLPF是在有效低通滤波和可接受的振铃特性之间的较好折中。
4.2.1构造滤镜
imbutterworthflpf.m
function ff=imbutterworthflpf(I,freq,n)
% imbutterworthflpf函数 构造布特沃斯的频域低通滤波器
% I参数 输入的灰度图像
% freq参数 低通滤波器的截止频率
% n参数 阶数
% 返回值 ff 与I等大的频域滤镜
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j) = 1/(1 + (sqrt((i - M/2)^2 + (j - N/2)^2)/freq)^(2*n));
end
end
4.2.2 应用
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
%生成滤镜 截止频率为20,阶数为2
ff = imbutterworthflpf(img,20,2);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为20,阶数为5
ff = imbutterworthflpf(img,20,5);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80,阶数为2
ff = imbutterworthflpf(img,80,2);
out2 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80,阶数为5
ff = imbutterworthflpf(img,80,5);
out3 = imfreqfilt(img,ff);
figure(1);
subplot(1,5,1);
imshow(img);
title('原图');
subplot(1,5,2);
imshow(out);
title('freq = 20,n = 2');
subplot(1,5,3);
imshow(out1);
title('freq = 20,n = 5');
subplot(1,5,4);
imshow(out2);
title('freq = 80,n = 2');
subplot(1,5,5);
imshow(out3);
title('freq = 80,n = 5');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
f4 = fft2(out3);
f4 = abs(fftshift(f4)); % 频谱
f4 = log(1 + f4); %压缩频率的范围
figure(2)
subplot(1,5,1);
imshow(f,[]);
title('原图对应的频谱');
subplot(1,5,2);
imshow(f1,[]);
title('freq = 20,n = 2的频谱');
subplot(1,5,3);
imshow(f2,[]);
title('freq = 20,n = 5的频谱');
subplot(1,5,4);
imshow(f3,[]);
title('freq = 80,n = 2的频谱');
subplot(1,5,5);
imshow(f4,[]);
title('freq = 80,n = 5的频谱');
4.3 高斯低通滤波器(GLPF)
![]()
D(u,v)为距频率中心的距离,σ是关于中心的扩展度的度量。令σ = D0,可以使介绍介绍中的表达式比较统一。即:
![]()
D0为截止频率。当D(u,v) = D0时,GLPF下降到其最大值的0.607处。

D0越大,通过的高通越大,清晰度越高。
GLPF中没有振铃现象。
4.3.1 生成滤镜
imgaussflpf.m
function ff=imgaussflpf(I,sigma)
% imgaussflpf函数 构造高斯的频域低通滤波器
% I参数 输入的灰度图像
% sigma参数 高斯函数的sigma
% 返回值 ff 与I等大的频域滤镜
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j) = exp(-((i - M/2).^2 + (j - N/2).^2) / 2 /(sigma.^2));
end
end
4.3.2 应用
Gauss_LPF.m
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
%生成滤镜 截止频率为20
ff = imgaussflpf(img,20);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为40
ff = imgaussflpf(img,40);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80
ff = imgaussflpf(img,80);
out2 = imfreqfilt(img,ff);
figure(1);
subplot(1,4,1);
imshow(img);
title('原图');
subplot(1,4,2);
imshow(out);
title('sigma = 20');
subplot(1,4,3);
imshow(out1);
title('sigma = 40');
subplot(1,4,4);
imshow(out2);
title('sigma = 80');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
figure(2)
subplot(1,4,1);
imshow(f,[]);
title('原图对应的频谱');
subplot(1,4,2);
imshow(f1,[]);
title('sigma = 20的频谱');
subplot(1,4,3);
imshow(f2,[]);
title('sigma = 40的频谱');
subplot(1,4,4);
imshow(f3,[]);
title('sigma = 80的频谱');


由图可知,sigma越大,截止频率越大,通过的高频越多,图像越清晰。
五、使用频率域滤波器锐化图像
图像的锐化可在频率域通过高通滤波器来实现,高通滤波会衰减傅里叶变换中的低频成分而不会扰乱高频信息。
高频通过,低频衰减,处理后的图像比原始图像少灰度级的平滑过渡而突出边缘等细节部分。
高通滤波器可从低通滤波器得到:
![]()
HLP(u,v)是低通滤波器的传递函数。
5.1 理想高通滤波器(IHPF)
二维理想高通滤波器定义为:



代码与理想低通滤波相似,只需要改动imidealflpf.m中的部分代码,即滤波器函数H(u,v)的内容,将函数命名再改动一下即可。不再赘述。
5.2 布特沃斯高通滤波器(BHPF)
5.3 高斯高通滤波器(GHPF)
5.3.1 生成滤镜
imgaussfhpf.m
function ff=imgaussfhpf(I,sigma)
% imgaussfhpf函数 构造高斯的频域低通滤波器
% I参数 输入的灰度图像
% sigma参数 高斯函数的sigma
% 返回值 ff 与I等大的频域滤镜
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j) = 1 - exp(-((i - M/2).^2 + (j - N/2).^2) / 2 /(sigma.^2));
end
end
5.3.2 应用
Gauss_HPF.m
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
%生成滤镜 截止频率为20
ff = imgaussfhpf(img,20);
out = imfreqfilt(img,ff);
%生成滤镜 截止频率为40
ff = imgaussfhpf(img,40);
out1 = imfreqfilt(img,ff);
%生成滤镜 截止频率为80
ff = imgaussfhpf(img,80);
out2 = imfreqfilt(img,ff);
figure(1);
subplot(1,4,1);
imshow(img);
title('原图');
subplot(1,4,2);
imshow(out);
title('sigma = 20');
subplot(1,4,3);
imshow(out1);
title('sigma = 40');
subplot(1,4,4);
imshow(out2);
title('sigma = 80');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
f2 = fft2(out1);
f2 = abs(fftshift(f2)); % 频谱
f2 = log(1 + f2); %压缩频率的范围
f3 = fft2(out2);
f3 = abs(fftshift(f3)); % 频谱
f3 = log(1 + f3); %压缩频率的范围
figure(2)
subplot(1,4,1);
imshow(f,[]);
title('原图对应的频谱');
subplot(1,4,2);
imshow(f1,[]);
title('sigma = 20的频谱');
subplot(1,4,3);
imshow(f2,[]);
title('sigma = 40的频谱');
subplot(1,4,4);
imshow(f3,[]);
title('sigma = 80的频谱');
实验结果:


小结:
高斯高通滤波器可以较好的提取图像中的边缘信息;
sigma越小,截止频率越低,通过的低频成分越多,边缘提取越不精确,会包含更多的非边缘信息;反之,sigma越大,边缘提取越精确,但可能包含不完整的边缘信息。
5.4 拉普拉斯滤波器
在第三章,已经使用过拉普拉斯算子对空间域的图像进行增强。现在使用拉普拉斯算子在频率域对图像进行增强。频域的拉普拉斯滤波器由下述函数确定:
![]()

5.4.1 生成滤镜
laplacehpf.m
function ff=laplacehpf(I)
% laplacehpf函数 构造laplace滤波器
% I参数 输入的灰度图像
% 返回值 ff 与I等大的频域滤镜
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j) = -4.*(pi.^2).*((i - M/2).^2 + (j - N/2).^2);
end
end
5.4.2 实现
img = imread('C:\Users\win\Desktop\fence-climbing.jpg');
img = rgb2gray(img);
%生成滤镜
ff = laplacehpf(img);
out = imfreqfilt(img,ff);
figure(1);
subplot(1,2,1);
imshow(img);
title('原图');
subplot(1,2,2);
imshow(out);
title('laplace滤波图像');
%展示频域的频谱
f = fft2(img);
f = abs(fftshift(f)); % 频谱
f = log(1 + f); %压缩频率的范围
f1 = fft2(out);
f1 = abs(fftshift(f1)); % 频谱
f1 = log(1 + f1); %压缩频率的范围
figure(2)
subplot(1,2,1);
imshow(f,[]);
title('原图对应的频谱');
subplot(1,2,2);
imshow(f1,[]);
title('laplace滤波图像对应的频谱');
5.5 锐化滤波器
前面介绍过:F(0,0),即原点处的傅里叶变换值为原图像f(x,y)的平均灰度级。可以看到F(0,0)的值是非常大的。将F(0,0)称为直流分量,直流分量比其他的成分要大好几个数量级。所以,这也就是傅里叶谱为什么需要使用对数变换才能看清楚的原因。
对于高通滤波器而言,由于直流分量被衰减,所以,所得到的图像的动态范围是非常狭窄的,也就造成了图像偏灰。
锐化滤波器是保持直流(DC)分量,对别的部分进行增幅,可以增强图像的细节。通用公式如下:

即,先将原图的傅里叶谱F(u,v)保留下来,再加上高通滤波器的结果HHP(u,v)F(u,v),所得到的图像就是锐化后的图像了。为了调整锐化程度,引入了两个变量k1、k2。
k1 >= 0控制距原点的偏移量,即调整直流分量的衰减程度;
k2 >= 0控制高频的贡献,即调整高频分量的增幅程度。
六、选择滤波器
高通和低通滤波器对图像进行处理,它们都是在整个图像的频率矩阵上操作,但是在很多应用中,我们感兴趣是处理指定的频段或频率矩形的小区域,因此需要使用选择性滤波,选择性滤波主要有两类:
- 带阻滤波器和带通滤波器
- 陷波滤波器
6.1 带阻和带通滤波器
所谓“带阻”就是阻止频谱中某一频带范围的分量通过,其他频率成分不受影响。

带通滤波器是由带阻滤波器得到的:
![]()

带阻滤波器常用于处理含有周期性噪声的图像。周期性噪声可能由多种因素引入,如图像获取系统中的电子元件等。
这里以高斯带阻滤波器为例进行说明。
高斯带阻滤波器的实现:
imgaussbrf.m
function ff=imgaussbrf(I,freq,width)
% imgaussbrf函数 构造高斯带阻滤波器
% I参数 输入的灰度图像
% freq参数 截止频率
% width参数 阻带宽度
% 返回值 ff 与I等大的频域滤镜
[M,N]=size(I);
ff=ones(M,N);
for i=1:M
for j=1:N
ff(i,j) = 1 - exp(-((((i - M/2).^2 + (j - N / 2).^2) - freq.^2) / (sqrt((i - M/2).^2 + (j - N / 2).^2) * width)).^2); %gauss带阻滤波器公式
end
end
Gauss_br_filter.m
img = imread('C:\Users\win\Desktop\dog.jpg');
img = rgb2gray(img);
[M,N] = size(img);
I = img;
for i = 1:M
for j = 1:N;
I(i,j) = I(i,j) + 20 * sin(20 * i) + 20 * sin(20 * j); %给原图像添加周期性噪声
end
end
%得到频谱
f = fft2(img);
f = abs(fftshift(f)); %频谱
f = log(1 + f); %压缩频率范围
f1 = fft2(I);
f1 = abs(fftshift(f1)); %频谱
f1 = log(1 + f1); %压缩频率范围
%带阻滤波
ff = imgaussbrf(I,150,120); % 构造带阻滤波器,截止频率为50,阻带宽度为5
out = imfreqfilt(I,ff); % 带阻滤波
figure();
subplot(3,2,1);
imshow(img);
title('原图');
subplot(3,2,2);
imshow(I);
title('added noise');
subplot(3,2,3);
imshow(f,[]);
title('原图频谱');
subplot(3,2,4);
imshow(f1,[]);
title('added noise 频谱');
subplot(3,2,5);
imshow(ff,[]);
title('高斯带阻滤波器');
subplot(3,2,6);
imshow(out,[]);
title('带阻滤波结果');
实验结果:

可以看到周期噪声在频率域被很好的消除了,这样的效果在空间域是很难实现的。
6.2 陷波滤波器
陷波带阻滤波器也用于去除周期噪声,虽然带阻滤波器也能可以去除周期噪声,但是带阻滤波器对噪声以外的成分也有衰减。而陷波带阻滤波器主要对某个点进行衰减,对其余的成分不损失。

可以看到,图像伴随着周期性噪声,从其频谱中也能看出来噪声在哪里(用红圈圈出来的)。
由于傅里叶的周期性,傅里叶频谱上不可能单独存在一个点的噪声,而是关于原点对称的噪声对,因此,一个中心位于(u0,v0)的陷波在位置(-u0,-v0)必须有一个对应的陷波。
陷波带阻滤波器可以用中心已被平移到陷波滤波器中心高通滤波器的乘积来构造。一般形式为:

Hk(u,v)和Hk(u,v)是高通滤波器,它们的中心分别是(uk,vk)和(-uk,-vk)。这些中心是根据频率中心(M/2,N/2)确定的。对每个滤波器,距离的计算由下式执行:

例如,下面是一个n阶布特沃斯陷波带阻滤波器,它包含三个陷波对:

常数D0k对每队陷波对都是相同的,但对于不同的陷波对,可以不同。
针对上图,设计布特沃斯陷波带阻滤波器,进行噪声的去除。
实验结果:

图一为布特沃斯陷波带阻滤波器乘以傅里叶变换后的结果,图二维滤波后的图像。可以很明显的看到噪声被有效的去除,原图像的画质明显提高。
陷波带通滤波器可由陷波带阻滤波器得到:
![]()









