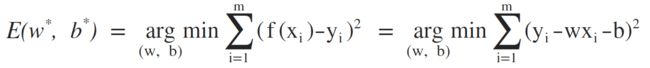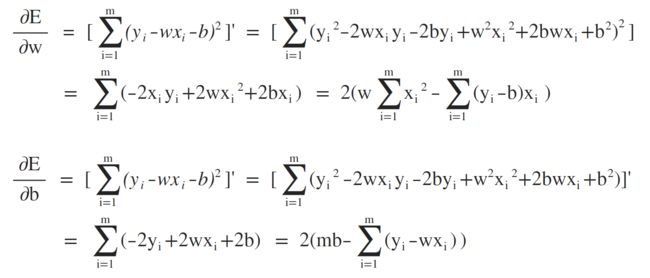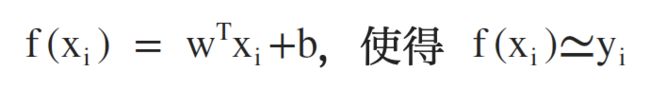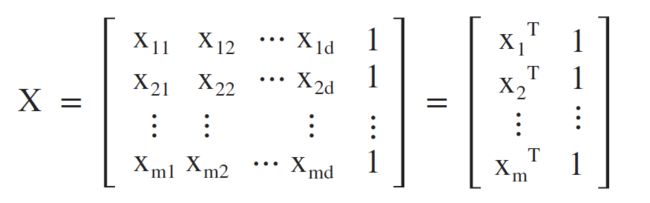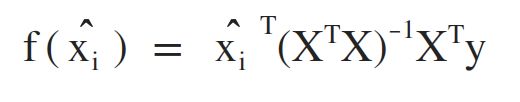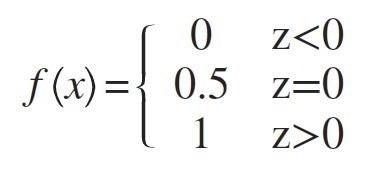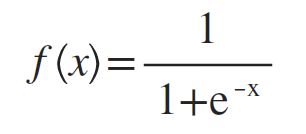1. 线性模型
基本形式:给定由d个属性描述的样本 x = (x1; x2; ......; xd),其中,xi是x在第i个属性上的取值,则有:
f(x) = w1x1 + w2x2 + ...... + wdxd + b
令w=(w1; w2; ......; wd),x = (x1; x2; ......; xd),使用矩阵乘法写为向量形式:
f(x) = wTx + b
在w和b的值确定后(w=(w1; w2; ......; wd)),整个模型就得以确定,其中,权重向量w可以直观表达各个属性的重要性。
2. 单一变量线性回归(Single Variable Linear Regression)
给定数据集 D = {(x1, y1), (x2, y2), (x3, y3), ......, (xm, ym)},其中 xi = (xi1, xi2, xi3, ......, xid),yi ∈ R,线性回归想要学到一个线性模型,以尽可能准确地预测实值输出标记。
首先考虑最简单的情况:输入的属性数目为1
目标:
误差函数(均方误差):
基于均方误差最小化进行模型求解的方法称之为:最小二乘法。
所以,求解w和b的值,使得E(w, b)最小化的过程,称之为线性回归的最小二乘参数估计,将E(w, b) 分别对w和b进行求导:
故w和b的最优闭式解为:
附:对于离散属性,可以对其进行连续化处理,例如,[0, 1] 表示从低到高,则可以使用 [0, 0.5, 1] 来分别表示低、中、高。如果离散属性间属于无序关系,假定有k个属性,则可以转化为K维向量,例如,白人、黑人、黄人对应 (0, 0, 1)、(0, 1, 0)、(1, 0, 0)。
3. 多元线性回归(Multivariate Linear Regression)
从单一变量线性回归推广至更一般的情形:数据集D中的样本由d个属性描述,即:多元变量线性回归。
目标:
令 w = (w; b),将数据集D表示为一个 m * (d+1) 的矩阵X,最后一个元素恒置为1,故有:
令标记为向量形式 y = (y1; y2; ......; ym),则有:
故令:
求导:
最后求得的多元线性回归模型为:
4. 对数几率回归 (Logistic Regression)
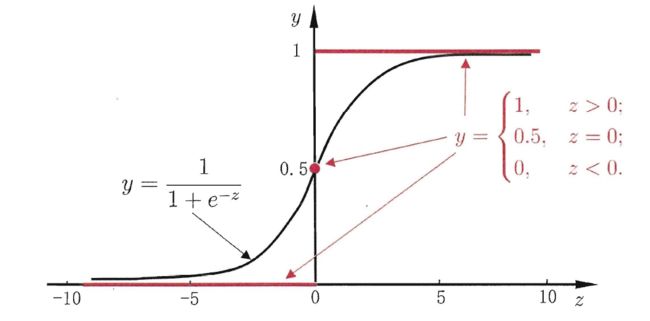
阶跃函数 (Unit-step Function):
然而阶跃函数不连续,无法作为替代函数使用,所以选择使用Sigmoid函数来代替阶跃函数:
将 f(x)=wTx+b 代入Sigmoid函数:
可以推出:
从上面推导的最终结果可以看出,y为输入量x被模型预测为正例的可能性,相应的,1-y则是被预测为反例的可能性,所以 ln(y/1-y) 被称之为对数几率(log odds, logit),所以该模型称为对数几率回归,虽然基于回归,但是实现的功能却是分类,同线性回归一样,当w和b的值确定,模型就得以确定。
特点:
- 直接对分类结果可能性进行建模,无需事先假设数据分布;
- 不仅预测类别,还可以得到近似概率预测;
- logit函数时任意阶可导的凸函数,数学性质优良,很多数值优化算法可以直接用于求取最优解。