4月17 【多方内容总结】大模块：车辆检测，车道线检测，车辆压线判别

大模块：车辆检测，车道线检测，车辆压线判别。

思路一：1.车道实线检测部分，虽然用Hough变换可以检测出不错的实线效果，但是需要每张图自己去调参，因为opencv算法已经集成好了，只需要调用即可。所以检测实线我们需要自己设定一个指标，就是实际Hough函数的参数构成的数组，我们标定测量车道线的实际结果，这个时候会有一组参数，然后我们和每组参数得到的车道线进行loss设计，这实际好的车道线和各组参数预测出来的车道线显然是有区别的，但是这个区别需要去建模得到一个指标，一个loss function，这样在任意图片当中，设计一个函数去遍历整个参数组，得到最佳的车道实线输出图。

通过loss function来得到一组最优的hough参数，实际上，还是需要根据不同的场景图片来调整，没有解决根本问题。

之前python通过一个dictionary来存当前帧图片当中的车道线直线的像素坐标值(y:x)，如果有好几帧的话，那么对于内存来讲是压力很大的，所以这里可以用一个滑动窗口的数据结构来动态分配字典数据，用两个索引，来存储前后好几帧的车道线像素的坐标，即下一帧的车道线的像素坐标可以更好地存在字典当中。

链接：https://blog.csdn.net/u010712012/article/details/87477554

2.虚线的检测，通过二值图像找到的白色像素点构成的集合，和下一个白色像素集合的线的斜率是一样的，我们可以给这个虚线打上标签，说明是虚线就可以。

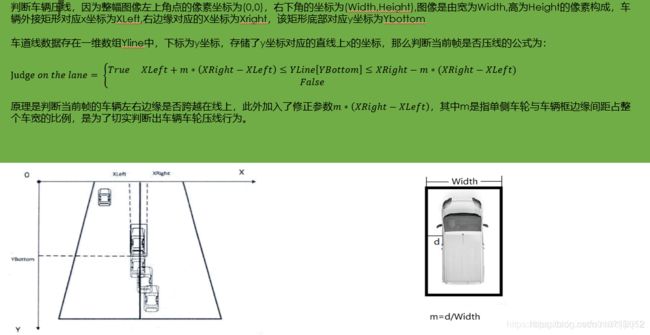
3、压线： 是否能够把检测到的车道直线左右扩充成车道带，然后再和bbox进行IOU计算，设定一个IOU阈值，这里需要用多张图片试验，得到一个比较适合的阈值，这是第一个条件，在满足第一个条件的前提下，再判断连续几帧bbox和车道带是否都超过了第一个条件的阈值，那么我们把这个几帧的图片的帧数当做第二个条件的阈值。通过这两个条件联合判断，判断压线。

3、车辆变道识别：需要把压线的情况当做触发条件，然后抽取前面几秒的和后面几秒的图片帧进行检测车辆的轨迹跟踪

Hough变换的嘴强解析

https://blog.csdn.net/linxid/article/details/78545678?depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1&utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromBaidu-1

https://blog.csdn.net/u010712012/article/details/86104053

Hough变换直线检测的Matlab实现
通过Hough在二值图像中检测直线需要以下3个步骤。
·>(1)利用hough()函数执行霍夫变换，得到霍夫矩阵。
·>(2)利用houghpeaks()函数在霍夫矩阵中寻找峰值点。
·>(3)利用houghlines()函数在之前2步结果的基础上得到原二值图像中的直线信息。

霍夫变换–Hough
调用形式：
[H,theta,rho]=hough(BW,param1,value1,param2,value2)

参数说明：
·BW是边缘检测后的二值图像；
·可选参数对param1,value1和param2,value2的合法取值如下：

返回值：
·H是变换得到的霍夫矩阵
·θ,ρ 分别对应于Hough矩阵每一列和每一行的θ,ρ 值组成的向量。

补充：[m,n] = size(X)

补充：norm的用法，matlab  help norm 
NORM   Matrix or vector norm.
For matrices...
对于矩阵...
NORM(X) is the largest singular value of X, max(svd(X)).
NORM(X)是X的最大奇异值
NORM(X,2) is the same as NORM(X).
NORM(X,1) is the 1-norm of X, the largest column sum,
          = max(sum(abs(X))).
NORM(X,inf) is the infinity norm of X, the largest row sum,
          = max(sum(abs(X'))).
NORM(X,'fro') is the Frobenius norm, sqrt(sum(diag(X'*X))).
NORM(X,P) is available for matrix X only if P is 1, 2, inf or 'fro'.

For vectors...
对于向量...
NORM(V,P) = sum(abs(V).^P)^(1/P).
返回向量A的p范数
NORM(V) = norm(V,2).
返回向量A的2范数，即欧几里德范数。二范数等价于平方和开平方，Sqrt(X1^2+X2^2+...+Xn^2) 

寻找峰值–houghpeaks
调用形式：
peaks=houghpeaks(H,numpeaks,param1,value1,param2,value2)

参数说明：
·H是hough()函数得到的霍夫矩阵
·numpeaks是要寻找的峰值数目，默认为1
·可选参数对param1,value1和param2,value2的合法取值如下：

返回值：
·peaks是一个Q×2的矩阵，每行的两个元素分别是某一峰值点再hough矩阵中的行、列索引，Q为找到的峰值点的数目。

提取直线段–houghlines
调用形式：
lines=houghlines(BW,theta,rho,peaks,param1,value1,param2,value2)

参数说明：
·BW是边缘检测后的二值图像
·theta,rho分别对应于Hough矩阵每一列和每一行的θ和ρθ和ρ值组成的向量。有hough()函数返回。
·peaks是一个包含峰值点信息的Q×2Q×2的矩阵，由houghpeaks()函数返回。
·可选参数对param1,value1和param2,value2的合法取值如下：

    I  = imread('circuit.tif');
    rotI = imrotate(I,33,'crop');
    BW = edge(rotI,'canny');
    [H,T,R] = hough(BW);
    imshow(H,[],'XData',T,'YData',R,'InitialMagnification','fit');
    xlabel('\theta'), ylabel('\rho');
    axis on, axis normal, hold on;
    P  = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
    x = T(P(:,2)); 
    y = R(P(:,1));
    plot(x,y,'s','color','white');

    % Find lines and plot them
    lines = houghlines(BW,T,R,P,'FillGap',5,'MinLength',7);
    figure, imshow(rotI), hold on
    max_len = 0;
    for k = 1:length(lines)
        xy = [lines(k).point1; lines(k).point2];
        plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','green');

        % plot beginnings and ends of lines
        plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
        plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');

        % determine the endpoints of the longest line segment 
        len = norm(lines(k).point1 - lines(k).point2);
        if ( len > max_len)
          max_len = len;
          xy_long = xy;
        end
    end

    % highlight the longest line segment
    plot(xy_long(:,1),xy_long(:,2),'LineWidth',2,'Color','cyan');

这里的Hough空间域就像上面的图，如果随便给我一张图片，我要检测出所有的车道线，那么就是在找Hough参数空间中那个二维累加器中找到峰值，也就是极值，那些极值就是可以被检测原图片的直线，那么将参数空间反映射回图像空间，就能知道哪些地方是直线了，虚线和直线的区别就在于一个阈值，这些参数空间的极值点到底我们选不选，有些极值点是长线段实线，有些极值点可能就是短线段，就是车道虚线，那么我们怎么通过Hough空间的图像判断实线与虚线呢？

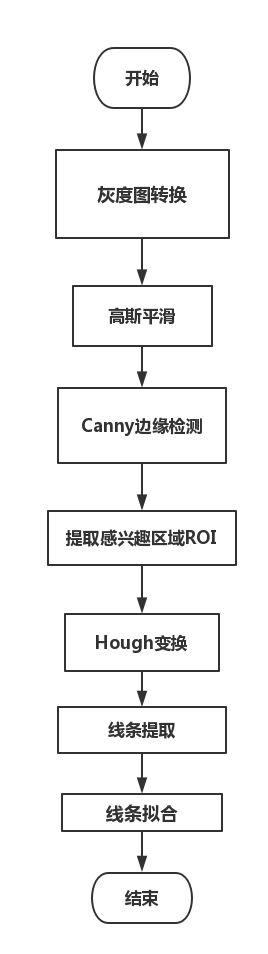
经典的流程

https://blog.csdn.net/u010712012/article/details/84780943

https://github.com/zengdiqing1994/Highway_violation_detection

FCM聚类

模糊C均值（Fuzzy C-means）算法简称FCM算法，是一种基于目标函数的模糊聚类算法，主要用于数据的聚类分析。理论成熟，应用广泛，是一种优秀的聚类算法。

https://blog.csdn.net/on2way/article/details/47087201
链接：https://blog.csdn.net/u010712012/article/details/87952752

一个样本属于结果的这种相似的程度称为样本的隶属度，一般用u表示，表示一个样本相似于不同结果的一个程度指标。

kmeans的类中心是怎么更新的，一般最简单的就是找到属于某一类的所有样本点，然后这一类的类中心就是这些样本点的平均值。

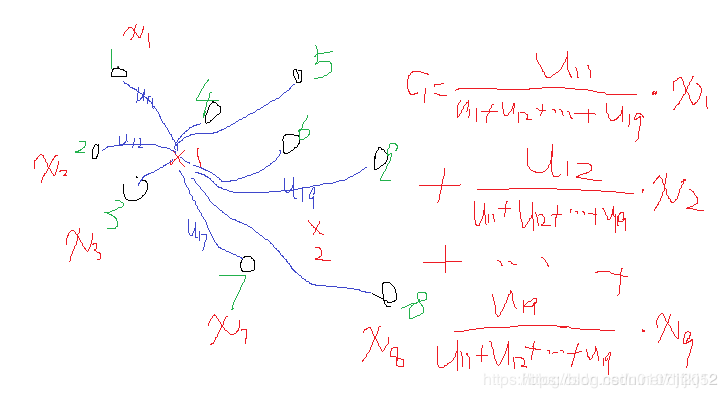
那么FCM类中心怎么样了？看式子可以发现也是一个加权平均，类i确定后，首先将所有点到该类的隶属度u求和，然后对每个点，隶属度除以这个和就是所占的比重，乘以xj就是这个点对于这个类i的贡献值了。画个形象的图如下：

数据集用的是iris数据，有需要数据的朋友可以调用sklearn.load_iris。或者下载下来

from pylab import *
from numpy import *
import pandas as pd
import numpy as np
import operator
import math
import matplotlib.pyplot as plt
import random

# 数据保存在.csv文件中
df_full = pd.read_csv("iris.csv")
columns = list(df_full.columns)
features = columns[:len(columns) - 1]
# class_labels = list(df_full[columns[-1]])
df = df_full[features]
# 维度
num_attr = len(df.columns) - 1
# 分类数
k = 3
# 最大迭代数
MAX_ITER = 100
# 样本数
n = len(df)  # the number of row
# 模糊参数
m = 2.00


# 初始化模糊矩阵U
def initializeMembershipMatrix():
    membership_mat = list()
    for i in range(n):
        random_num_list = [random.random() for i in range(k)]
        summation = sum(random_num_list)
        temp_list = [x / summation for x in random_num_list]  # 首先归一化
        membership_mat.append(temp_list)
    return membership_mat


# 计算类中心点
def calculateClusterCenter(membership_mat):
    cluster_mem_val = zip(*membership_mat)
    cluster_centers = list()
    cluster_mem_val_list = list(cluster_mem_val)
    for j in range(k):
        x = cluster_mem_val_list[j]
        xraised = [e ** m for e in x]
        denominator = sum(xraised)
        temp_num = list()
        for i in range(n):
            data_point = list(df.iloc[i])
            prod = [xraised[i] * val for val in data_point]
            temp_num.append(prod)
        numerator = map(sum, zip(*temp_num))
        center = [z / denominator for z in numerator]  # 每一维都要计算。
        cluster_centers.append(center)
    return cluster_centers


# 更新隶属度
def updateMembershipValue(membership_mat, cluster_centers):
    #    p = float(2/(m-1))
    data = []
    for i in range(n):
        x = list(df.iloc[i])  # 取出文件中的每一行数据
        data.append(x)
        distances = [np.linalg.norm(list(map(operator.sub, x, cluster_centers[j]))) for j in range(k)]
        for j in range(k):
            den = sum([math.pow(float(distances[j] / distances[c]), 2) for c in range(k)])
            membership_mat[i][j] = float(1 / den)
    return membership_mat, data


# 得到聚类结果
def getClusters(membership_mat):
    cluster_labels = list()
    for i in range(n):
        max_val, idx = max((val, idx) for (idx, val) in enumerate(membership_mat[i]))
        cluster_labels.append(idx)
    return cluster_labels


def fuzzyCMeansClustering():
    # 主程序
    membership_mat = initializeMembershipMatrix()
    curr = 0
    while curr <= MAX_ITER:  # 最大迭代次数
        cluster_centers = calculateClusterCenter(membership_mat)
        membership_mat, data = updateMembershipValue(membership_mat, cluster_centers)
        cluster_labels = getClusters(membership_mat)
        curr += 1
    print(membership_mat)
    return cluster_labels, cluster_centers, data, membership_mat


def xie_beni(membership_mat, center, data):
    sum_cluster_distance = 0
    min_cluster_center_distance = inf
    for i in range(k):
        for j in range(n):
            sum_cluster_distance = sum_cluster_distance + membership_mat[j][i] ** 2 * sum(
                power(data[j, :] - center[i, :], 2))  # 计算类一致性
    for i in range(k - 1):
        for j in range(i + 1, k):
            cluster_center_distance = sum(power(center[i, :] - center[j, :], 2))  # 计算类间距离
            if cluster_center_distance < min_cluster_center_distance:
                min_cluster_center_distance = cluster_center_distance
    return sum_cluster_distance / (n * min_cluster_center_distance)


labels, centers, data, membership = fuzzyCMeansClustering()
print(labels)
print(centers)
center_array = array(centers)
label = array(labels)
datas = array(data)

# Xie-Beni聚类有效性
print("聚类有效性：", xie_beni(membership, center_array, datas))
xlim(0, 10)
ylim(0, 10)
# 做散点图
fig = plt.gcf()
fig.set_size_inches(16.5, 12.5)
f1 = plt.figure(1)
plt.scatter(datas[nonzero(label == 0), 0], datas[nonzero(label == 0), 1], marker='o', color='r', label='0', s=10)
plt.scatter(datas[nonzero(label == 1), 0], datas[nonzero(label == 1), 1], marker='+', color='b', label='1', s=10)
plt.scatter(datas[nonzero(label == 2), 0], datas[nonzero(label == 2), 1], marker='*', color='g', label='2', s=10)
plt.scatter(center_array[:, 0], center_array[:, 1], marker='x', color='m', s=30)
plt.show()

竟然聚类的结果感觉和刚开始的好像差不多啊。不会被聚成一类？但是回过头来看这个算法，本身要得到的结果就是隶属度u（也就是各样本的权重）以及Ci聚类中心，有几个聚类中心就有几类，可以看到，还是挺准的。

但是这里有一个明显的问题就是

FCM算法需要手动设置需要聚类出来的类数，假设一条道路有6条车道线，那么K=6，不同的场景车道线数量不同。这让人想到了无监督学习中的Kmeans算法，他的缺点也是需要人工先确定K值，且该值和真实的数据分布未必吻合，也易受到噪声点的影响，容易陷入局部最值，并不能有力地求到全局最优。所以个人感觉只适合于道路清晰的高速公路上，一旦有多辆车在内做干扰，或者路面老旧导致车道线不清晰，FCM并不能算是一个非常鲁棒的算法。

但是不可否认的是，FCM聚类算法使用的边缘去重和结构化过滤方法还是很有借鉴意义，可以起到稳固车道线的作用，从而对后续的车辆压线判别模型奠定了基础。

车道线写成：y=kx+b

而且我们得到的（k，b）坐标轴，可以看出，在原图像坐标中的斜率为正的直线，都集中在右下角的点，很密集。而斜率负的很大的直线则分散在左上角而且距离比较大，按照聚类（物以类聚）的思想，应该是离得越远的点越没可能是一类。

但是不可否认的是，FCM聚类算法使用的边缘去重和结构化过滤方法还是很有借鉴意义，可以起到稳固车道线的作用，从而对后续的车辆压线判别模型奠定了基础。

而且我们得到的（k，b）坐标轴，可以看出，在原图像坐标中的斜率为正的直线，都集中在右下角的点，很密集。而斜率负的很大的直线则分散在左上角而且距离比较大，按照聚类（物以类聚）的思想，应该是离得越远的点越没可能是一类。

可以考虑把斜率的k=tanθ ，这里的角度在斜率比较小的时候差距不大，但是有可能在斜率很大的时候，多条线之间的角度差距也不大

因为每条线的theta都有具体的值,每一条线的θ 相减，如果角度差距超过设定的一个阈值的话，就代表不是一类，如果角度小于一类的，就看成是一类 就要看怎么和聚类的算法进行融合了

然后思考一下能不能把k，b坐标轴转变成ρ,θ 极坐标空间，然后看FCM聚类算法是否能够解决上述的角度截距的问题。【可能，后面如果转成极坐标空间更佳】