物体6D位姿的含义

6D是指6个自由度，代表了3个自由度的位置（也叫平移（Translation）），以及3个自由度的空间旋转。那么具体是如何变换的呢？

如果了解相机的内外参，就可以得到下面的表示：$T_c=R_{cw}\ast T_w+t_{cw}$，其中$R_{cw}$代表由世界系到相机系的旋转，$t_{cw}$代表由世界系到相机系的平移。

而物体的6D位姿，是指相机系下物体的$Rt$，也即将物体本身的坐标系当成世界系，变换到相机系的$Rt$，则可以得到下面的表示：$T_c=R_{cm}\ast T_m+t_{cm}$，其中$R_{cm}$代表由物体的世界系到相机系的旋转，$t_{cm}$代表由物体的世界系到相机系的平移。

具体一个例子，数据来自preprocessed LineMod dataset数据集，物体本身的坐标系，当成世界系，其坐标值为$T_m$：

相机坐标系，此时物体的坐标为$T_c$：

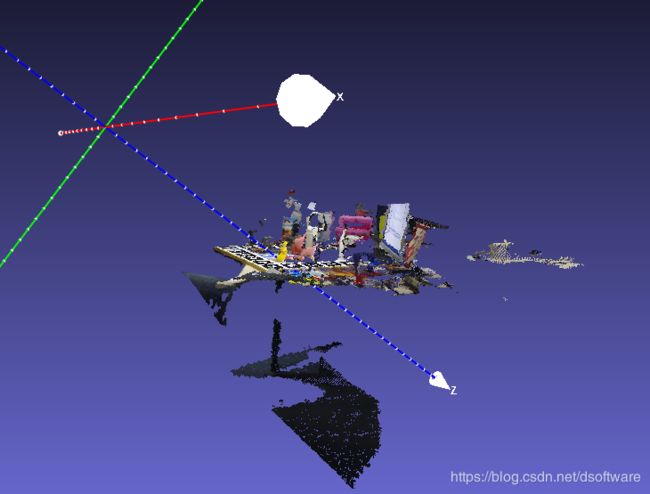
基于给定的GT的物体6D位姿：
cam_R_m2c: [0.09630630, 0.99404401, 0.05100790, 0.57332098, -0.01350810, -0.81922001, -0.81365103, 0.10814000, -0.57120699]，
cam_t_m2c: [-105.35775150, -117.52119142, 1014.87701320]，
使用$T_c=R_{cm}\ast T_m+t_{cm}$，将物体变换到相机系下如下图：

此时可以看到，根据物体的位姿$R_{c}m$和$t_{c}m$将物体由本身的世界系变换到了相机系下，叠加在一起的效果如下：

此时，也可以结合相机的内参K， cam_K: [572.4114, 0.0, 325.2611, 0.0, 573.57043, 242.04899, 0.0, 0.0, 1.0]，将物体投影到2d，如下图，可以看到也是正确的。

因此，物体的位姿是和物体本身的坐标系相关的，同一个相机系下，不同物体的位姿是不一样的；如果保持物体和相机的相对位置不变，则物体的位姿是不变的；如果物体不动，相机系发生了移动，则新的物体位姿需要在原来的基础上再叠加相机系的相对移动位姿$△R$和$△t$。

p.s.上文中使用的是preprocessed的LineMOD数据集，物体的3D模型中心在$(0,0,0)$位置，这里把原始的LineMOD数据集也测试一下。

同样是ape类别，其3D模型如下图。

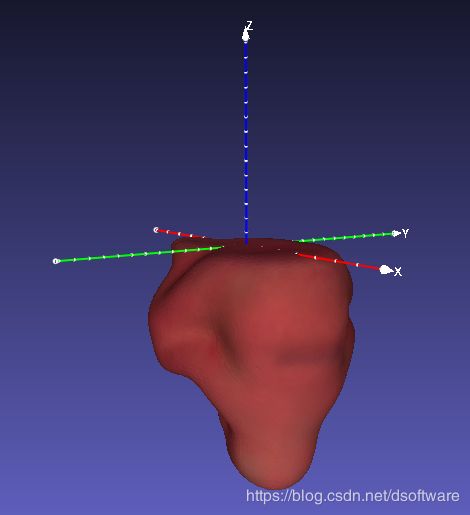
可以看到其与上文的3D模型差别了绕y轴旋转180°，也即旋转矩阵$R_{m{m}_o}=[-1,0,0,0,1,0,0,0,-1]$，并且旋转后的重心需要向坐标原点平移。原始物体的中心为$c_{m_o}=(4.5445,4.6495,-44.5433)$，因此$T_m=R_{m{m}_o}\ast T_{m_o}+t_{m{m}_o}$，其中$t_{m{m}_o}=c_m-R_{m{m}_o}\ast c_{m_o}$，而$c_m=(0,0,0)$为preprocessed后的物体的中心坐标，由此可得$t_{m{m}_o}=(4.5445,-4.6495,-44.5433)$

按照原始LineMOD提供的真值，有$T_c=R_{c{m}_o}\ast T_{m_o}+t_{c{m}_o}$，其中$R_{c{m}_o}$代表了由原始物体向相机系物体的旋转，$T_{m_o}$代表原始物体的坐标点，$t_{c{m}_o}$代表原始物体向相机系物体的平移。可以进行变换：
$T_c=[R_{c{m}_o}{t}_{c{m}_o}]\ast T_{m_o}$
$=[R_{c{m}_o}{t}_{c{m}_o}]\ast [R_{m{m}_o}^T-R_{m{m}_o}^T{t}_{m{m}_o}]\ast [R_{m{m}_o}{t}_{m{m}_o}]\ast T_{m_o}$
$=[R_{c{m}_o}{t}_{c{m}_o}]\ast [R_{m{m}_o}^T-R_{m{m}_o}^T{t}_{m{m}_o}]\ast T_m$
其中第二项是第三项的逆。

根据原始LineMOD提供的真值：
$R_{c{m}_o}$为：
-0.0963063 0.994044 -0.0510079
-0.573321 -0.0135081 0.81922
0.813651 0.10814 0.571207 r
$t_{c{m}_o}$为：
-111.814 -78.3622 1036.12
代入上式得到最终的preprocessed后的物体的$R_{cm}$$t_{cm}$，和preprocessed提供的真值是一致的。