【数据结构】邻接矩阵表示法的图的深度广度优先遍历递归和非递归遍历
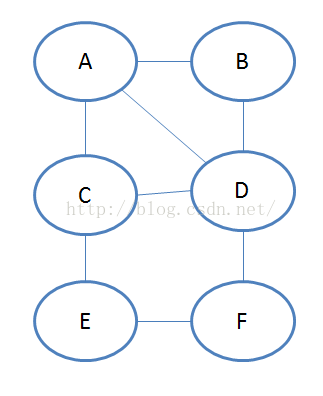
假设有以下结构的图:
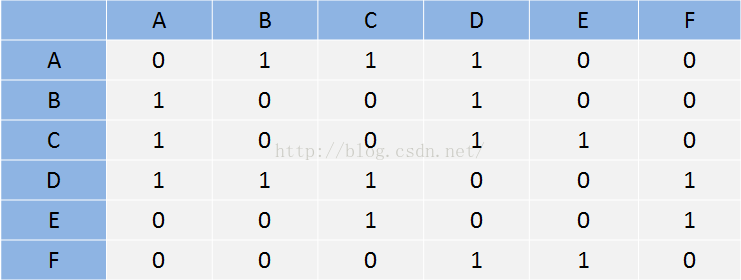
用邻接矩阵表示如下:
因为他是无向图,我们可以发现他的矩阵是对角对称的。矩阵中每一行每一列都可以看成是一个顶点,矩阵中的元素表示着该顶点与其他顶点的关系,当元素的值为1说明它与对应列的顶点有边相连,如果他们的值为0,表示他们没有边相连。下面我们来看看我们怎么遍历这个图。
1.深度优先遍历:
假设我们从A这个顶点开始遍历,当访问到A点的时候它会找与A相连的第一个顶点B(为什么B是第一个与A相连的顶点?请看矩阵),并且访问B,访问到B点,它会碰到到与B第一个相连的顶点A,但是A顶点已经访问过,他就去找与B相连的下一个顶点D,并且访问。访问到D的时候,他就会去找与D相连但是没有访问过的顶点E,并访问。访问了E,他又去寻找与E相连并且未被访问过的顶点F.访问F后,并访问F相连的节点,发现与F相连的节点都已被访问过。结束遍历。所以该无向图的深度遍历的顺序为:A->B->D->C->E->F
深度优先遍历我们可以用栈来模拟,并且我们要用一个数组来存储某个顶点是否被访问过,深度优先遍历的代码如下:
private static int matrix[][]=
{
{0,1,1,1,0,0},//A
{1,0,0,1,0,0},//B
{1,0,0,1,1,0},//C
{1,1,1,0,0,1},//D
{0,0,1,0,0,1},//E
{0,0,0,1,1,0}//F
};
//每个顶点的数据表示,方便查看
private static String str="ABCDEF";
public static void DFS(int line) {
Stack stack=new Stack();
boolean[] isVisit=new boolean[6];//保存每个顶点是否访问过
Arrays.fill(isVisit, false);
stack.push(line);//第一个顶点入栈
int temp;
int cur = 0;
boolean isFirst;
while(!stack.empty()){//如果栈不为空
temp=stack.pop();
if(!isVisit[cur])
System.out.print(str.charAt(temp)+" ");
isFirst=true;//记录元素在矩阵的行中是否为第一个节点
isVisit[temp]=true;
for (int i = 0; i 2.广度优先遍历
广度优先遍历的思路是,先把与之相连的顶点都访问一遍,再把该顶点的顶点访问一遍,以此类推。在这里就不详细说明了。该图的广度优先遍历的顺序是:A->B->C->D->E->F
根据广度优先遍历的特点,我们用队列来模拟,代码如下:
private static int matrix[][]=
{
{0,1,1,1,0,0},//A
{1,0,0,1,0,0},//B
{1,0,0,1,1,0},//C
{1,1,1,0,0,1},//D
{0,0,1,0,0,1},//E
{0,0,0,1,1,0}//F
};
//每个顶点的数据表示,方便查看
private static String str="ABCDEF";
/**
* 非递归广度优先遍历邻接矩阵图
* @param line 遍历的起点
*/
public static void BFS(int line)
{
boolean[] isVisit=new boolean[6];//保存每个顶点是否访问过
Arrays.fill(isVisit, false);
int temp;
Queue queue=new LinkedList();
queue.offer(line);//插入队列
while (!queue.isEmpty()) {
temp=queue.poll();
if(!isVisit[temp])//如果没有访问过
System.out.print(str.charAt(temp)+" ");//打印结果
isVisit[temp]=true;//打完结果设为已访问
for (int i = 0; i < isVisit.length; i++) {
if(matrix[temp][i]==1&&!isVisit[i])
{
queue.offer(i);
}
}
}
}