Ising模型、QUBO 及 Chimera Graph（QPU 架构）介绍

Ising模型、QUBO 及 Chimera Graph（QPU 架构）介绍

【所有内容均是对官方文档的学习记录总结】

用 D-Wave QPU 来构建问题需要知道以下几个概念：目标函数、Ising 模型、二次无约束二值优化问题（QUBOs, quadratic unconstrained binary optimization problems）和图。这篇介绍这些概念。

目标函数

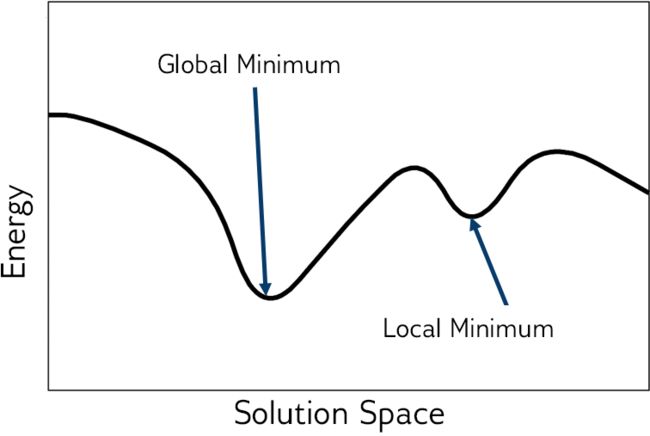
想要理解如何用D-Wave系统可以解决的问题形式来表述（问题），首先需要定义一个目标函数（objective function），用这个目标函数表示系统的能量，是表示qubits 的二值变量的函数。多数情况下，目标函数的能量越低，解就越好。有时任何低能态都是原始问题的可接受范围的解；只有对其他一些问题，必须是最优解才可以。通常最优解对应于解空间的 global minimum 能量。如图3.1所示。

Figure 3.1: Energy of objective function.

对于二次函数，每一项都有1或2个变量：

$$D=Ax+By+Cxy\text{\hspace{1em}(3.1)}$$

其中 $A,B,C$ 都是常量。单变量项（比如 $Ax$ and $By$）是线性的，表示偏置变量。两变量项（比如 $Cxy$）表示变量之间的关系是二次的。

Ising and QUBO

目标函数的两种形式为：Ising 和 QUBO，这两种模型之间的区别很小。

Ising 模型

Ising 模型是统计力学中常用的模型，变量有“自旋向上(spin up)（$\uparrow$）”和“自旋向下(spin down)（$\downarrow$）,这两个状态分别代表 $+1$ 和 $-1$.由耦合(couplings)表示的自旋之间的关系是相关或非相关。目标函数可以用如下Ising模型来表示：

$$E_{ising}(s)=\sum _{i=1}^N{h}_i{s}_i+\sum _{i=1}^N\sum _{j=i+1}^N{J}_{i,j}{s}_i{s}_j\text{\hspace{1em}(3.2)}$$

其中对应 qubit 偏置（bias）的线性系数是 $h_i$ ,对应耦合权重（coupling strengths）是 $J_{i,j}$。

QUBO

QUBO 问题通常用在计算机科学中，TRUE 和 FALSE 状态对应于1和0。一个QUBO问题是由上对对角矩阵 $Q$（$N\times N$的实值上三角矩阵）和 $x$（二元变量的向量）来定义的。最小化函数：

$$f(x)=\sum _i{Q}_{ii}{x}_i+\sum _{i<j}{Q}_{i,j}{x}_i{x}_j\text{\hspace{1em}(3.3)}$$

其中对角项$Q_{i,j}$是线性系数，非零的非对角项时的二次系数。可以用如下式子精确表示：

$$\underset{x\in \{0,1{\}}^n}{\min }{x}^{T}Qx.\text{\hspace{1em}(3.4)}$$

用标量表示法（后面表述通常都用的这一表示法），QUBO 的目标函数可以用如下式子表示：

$$E_{qubo}(a_i,b_{i,j};q_i)=\sum _i{a}_i{q}_i+\sum _{i<j}{b}_{i,j}{q}_i{q}_j\text{\hspace{1em}(3.5)}$$

表示法对比

图3.2 比较了 Ising 和 QUBO 的记号以及相关的术语。Ising 和 QUBO 的转换关系可以用下式表示（根据States也可以分析得出）：

$$s=q\cdot 2-1\text{\hspace{1em}(3.6)}$$

Figure3.2: Notation conventions.. 图3.2中的 Graph 在这里指的是无向图。 目标函数可以用 graphs 来表示。图是由节点（表示变量）和节点之间的连接（边）组成。

比如，两个变量的二次等式可以用如下式子来表示：

$$H(a,b)=5a+7ab-3b\text{\hspace{1em}(3.7)}$$

如图3.3所示，两个节点 $a$ 和 $b$ 的 bias 分别是 5 和 -3，节点之间的权重是 7. 在D-Wave系统中，无向图的节点就是 qubit ，无向图的边就是 couple 。

Figure3.3: Two-variable objective function.

---

D-Wave QPU 架构：Chimera

想要把 QUBO 或者 Ising 这样的目标函数转换成 D-Wave 系统能够处理的格式，首先我们要了解一下 D-Wave QPU 的布局。D-Wave QPU 是相互连接的 qubits 组成的晶格，虽然 qubit 之间是通过耦合连接的，但 D-Wave QPU 是不完全连接的。qubits 相互连接的结构称为 Chimera。

Chimera 结构是由 unit cells 相互连接而成，垂直（每列）的四个 qubit 和 水平（另外列）的四个 qubit 通过 couplers 连接，产生了一个 qubits 稀疏连接的晶格。如图 4.1。符号 $C_N$ 表示由 $N\times N$ 个 unit cells 组成的 Chimera 图。D-Wave 2000Q QPU 支持 $C_{16}$ Chimera 图：2048个qubit 映射到 $16\times 16$ unit cells 矩阵，每个 unit cells 有 8 个 qubits。在D-Wave QPU 中，可用于计算的一组 qubits 和 couplers 称为 working graph。通常在实际QPU中，working graph 的数量是少于 qubits 和 couplers 的数量的。（部分可能不起作用）

Figure 4.1: A 3x3 Chimera graph, denoted C3. Qubits are arranged in 9 unit cells.

Figure 4.2: Cross or column layout of qubits in a unit cell

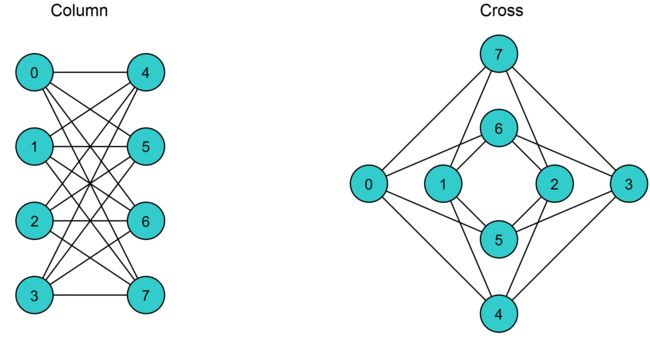
如图4.2，一个 unit cell 的布局可以是 cross 形式的也可以是 column 形式的。每个图中，都可以看到含有4个 qubits 的两组。每组（4个qubits）中的每一个qubit都和另外组的所有qubits相连接，但是不会和同一个组内的其他qubit相连接。在 unit cell 中，qubit 具有 二分图连通性（bipartite connectivity）。

表示目标函数的图中的 nodes 和 edges 可以转换为 Chimera 中的 qubits 和 couplers。在目标函数图中，每个逻辑 qubit 都可以由一个或多个物理 qubit 表示。把逻辑 qubits 映射物理 qubits 的过程称为 minor embedding。

【注】：通过SAPI可获取 minor embedding 的工具。也可以手动实现，在[Minor-Embedding a Problem onto the Chimera Graph] 这一部分会讲到。