点积和叉积在计算机图形学的应用
点积和叉积在计算机图形学中,是最为基础且重要的概念,初学者弄清它的概念的应用,是很重要的。最后一节,是为了加强理解记录,如果不看也是可以的,大家选择观看,有兴趣可以去看原视频,结合我的笔记。
前置知识
-
列向量
以下均采用列向量的表示方法,和线性代数书本上的行向量不同,采用列向量表示,则表达为列向量左乘矩阵,只是定义的不同,其他含义没有什么不同。列向量写法如下:
a → = ( x y z ) \overrightarrow{a} = \left( \begin{gathered} \begin{matrix} x \\ y \\ z \end{matrix} \end{gathered} \right) a=⎝⎛xyz⎠⎞ -
单位化
将向量的各分量除以向量的模即得单位向量,单位指模为1的向量。 -
行列式
行列式在数学中,是一个函数,其定义域为det的矩阵A,取值为一个标量,写作det(A)或 | A | 。行列式可以看做是有向面积(二维)或体积(三维)的概念在一般的欧几里得空间中的推广。
点积
点积在数学中,又称数量积(dot product; scalar product),是指接受在实数R上的两个向量并返回一个实数值标量的二元运算。它是欧几里得空间的标准内积。点积的结果是一个数。
a → ⋅ b → = ∣ a ∣ ∣ b ∣ c o s θ \overrightarrow{a} \cdot \overrightarrow{b} = \left| a \right| \left| b \right| cos {\theta} a⋅b=∣a∣∣b∣cosθ
相当于a向量的转置矩阵乘以向量b:
a → ⋅ b → = a → T b → \overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{a}^T \overrightarrow{b} a⋅b=aTb
以二维向量为例:
a → ⋅ b → = ( x a y a ) T ( x a y b ) = x a x b + y a y b \overrightarrow{a} \cdot \overrightarrow{b} = {x_{a}\choose y_{a}}^T {x_{a}\choose y_{b}} = x_{a}x_{b} + y_{a}y_{b} a⋅b=(yaxa)T(ybxa)=xaxb+yayb
几何意义
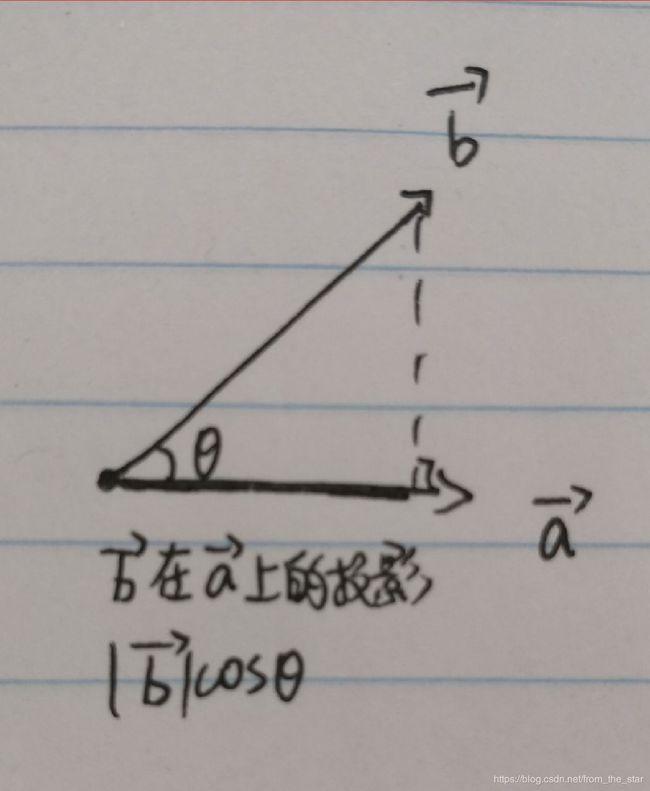
a向量在b向量上投影的长度 乘以 b向量的长度(模)就是 点积的结果。
点乘是存在交换律的,所以也等同于:
b向量在a向量上投影的长度 乘以 a向量的长度就是 点积的结果。
在图形学的应用
-
求两个向量的夹角
当 a → \overrightarrow{a} a与 b → \overrightarrow{b} b都是单位向量(单位化),两个向量点积就是 cos θ \cos {\theta} cosθ,在通过 arccos \arccos arccos 就可以求出夹角。 -
求投影
将 a → \overrightarrow{a} a单位化, a → ⋅ b → \overrightarrow{a} \cdot \overrightarrow{b} a⋅b就是 b → \overrightarrow{b} b在 a → \overrightarrow{a} a上的投影长度。
《计算机图形学》书上有这么一个举例,利用投影将向量w分解成两个向量和:
-
比较两个向量的接近程度(方向上)
也就是向量是否两个向量间的夹角大小,在聚光灯的效果计算中,可以根据点积来得到光照效果,如果点积越大,说明夹角越小,则物体离光照的轴线越近,光照越强。
也常会用来判断两向量是否为同方向:
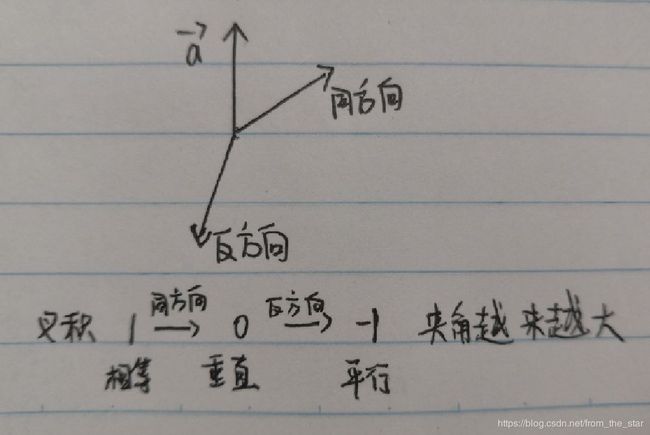
举个例子
叉积
向量积,数学中又称外积、叉积,物理中称矢积、叉乘,是一种在向量空间中向量的二元运算。与点积不同,它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。
∣ v → × w → ∣ = ∣ v ∣ ∣ w ∣ s i n θ \left| \overrightarrow{v} \times \overrightarrow{w} \right| = \left| v \right| \left| w \right| sin {\theta} ∣∣∣v×w∣∣∣=∣v∣∣w∣sinθ
这只确定了叉积的长度,众所周知向量有长度,还有方向的,方向为垂直于两个向量的方向,但是呢,垂直方向有两个。
这里我们采用右手螺旋定则确定方向。v到w的方向就是右手四指弯曲的方向,大拇指的方向就是叉积的方向。

二维向量的叉积是个标量,看起来违背了定义,先假设二维向量得出来的叉积是z,如果把二维向量看作成z轴值恒为0的三维向量,它们的叉积就 ( 0 , 0 , z ) T (0,0,z)^T (0,0,z)T,三维空间被压缩成了二维,叉积就只是一个标量了。
v → ⋅ w → = x v y w − y v x w \overrightarrow{v} \cdot \overrightarrow{w} = x_vy_w - y_vx_w v⋅w=xvyw−yvxw
三维向量的叉积的结果是个向量:
v → ⋅ w → = ( y v z w − z v y w z v x w − x v z w x v y w − y v x w ) \overrightarrow{v} \cdot \overrightarrow{w} = \left( \begin{gathered} \begin{matrix} y_v z_w - z_v y_w \\ z_vx_w - x_vz_w \\ x_vy_w - y_vx_w \end{matrix} \end{gathered} \right) v⋅w=⎝⎛yvzw−zvywzvxw−xvzwxvyw−yvxw⎠⎞
这个看起来很难记忆,我们随后再讲解。444额方法

几何意义
在二维空间,两个向量叉积就是两向量形成的平行四边形的面积,正负要引入Z轴,由右手螺旋定则确定,如果大拇指指向Z正轴就为正,反之为负;
在三维空间,两个向量叉积就是垂直于两向量形成的平面的向量(称为法向量)采用右手螺旋定则确定方向。v到w的方向就是右手四指弯曲的方向,大拇指的方向就是叉积的方向。
坐标系的问题
如果我们已知x坐标轴和y坐标轴,可以推导出z坐标轴。可能大家都听说过有左手坐标系和右手坐标系这两种说法,可以用x、y轴叉积与z轴的关系确定。
右手坐标系:
x → × y → = z → \overrightarrow{x} \times \overrightarrow{y} = \overrightarrow{z} x×y=z
左手坐标系:
x → × y → = − z → \overrightarrow{x} \times \overrightarrow{y} = -\overrightarrow{z} x×y=−z
在图形学的应用
- 二维空间判断左右
- 三维空间求法向量
法向量在计算图形学的应用很广泛,很多地方都会利用到,比如求已知入射角度 O B → \overrightarrow{OB} OB求一个平面的反射角度 B P → \overrightarrow{BP} BP。取平面上不共线的三个点ABC,求得法线
A B → × A C → = Z → ( 法 线 ) \overrightarrow{AB} \times \overrightarrow{AC} = \overrightarrow{Z} (法线) AB×AC=Z(法线)
B P → = O B → − Z → \overrightarrow{BP} = \overrightarrow{OB} - \overrightarrow{Z} BP=OB−Z
再举个例子
以线性变换去看点乘和叉乘
这部分我是基于B站的一部分的视频总结的,如果觉得作者讲解不够好,可以去看原视频。
点乘
先来看两向量的点乘另一种求法,a向量的转置矩阵乘以向量b:
a → ⋅ b → = a → T b → \overrightarrow{a} \cdot \overrightarrow{b} = \overrightarrow{a}^T \overrightarrow{b} a⋅b=aTb
以二维空间为例,定义两个基向量组成的矩阵

( 2 1 ) = 2 i → + j → \left( \begin{array}{c} 2 \\ 1 \end{array} \right)= 2\overrightarrow{i} + \overrightarrow{j} (21)=2i+j
点乘就是从二维空间到数轴的线性变换,将空间投影到给定的数轴来定义。
a → T \overrightarrow{a}^T aT矩阵作用就是,将基变量在 a → \overrightarrow{a} a上投影为两个数字,而不是向量,将此作为基变量去做线性变换,从而进行空间压缩。
叉乘
截了视频的两张图,

[ x y z ] \left[ \begin{array}{c} x \\ y \\ z\end{array} \right] ⎣⎡xyz⎦⎤表示一个随机变量,也可理解为一个为向量的变量。
上图是一个变量为向量的函数。根据v w 可以求常量 p

有没有觉得 p → \overrightarrow{p} p与 u → × v → \overrightarrow{u} \times \overrightarrow{v} u×v 叉积一模一样,我们从几何空间联系下它们。
先看左边, p → \overrightarrow{p} p与随机变量的点积,其实就随机变量在 p → \overrightarrow{p} p的投影长度,再乘以 p → \overrightarrow{p} p的模。
再看看右边,是一个行列式,表示这三个向量组成的立方体的体积大小。
我们再回顾下,体积的求法,高✖️底面积(u v 组成底面)
高为随机变量在平面垂直方向的投影长度。
然后回想下,叉积的定义,模长为两向量组成的平面面积,且为这个平面的法线。
p → \overrightarrow{p} p 和 这个叉积是不是就联系上了。
字丑的那些图都是我画的,除了一张小手手,请各位见谅,最后感谢我的首席插画师 yc君 画的那种小手手的插图,O(∩_∩)O哈哈~。




