常用的回归模型及其代码实现

线性回归（Linear Regression)

机器学习中最简单的回归模型，在一元回归模型中，形式为一元函数关系Y= Wx + b,称为单变量线性回归（Single Variable Linear Regression ）。简单来说就是用一元线性模型来拟合数据关系。当然，实际运用基本都是多变量的线性回归（Multi Variable Linear Regression）（单变量高中生都能拟合了），体现了多个输入自变量（特征变量）与输出因变量之间的关系。

其中a是系数，b是偏置。适用于建模线性可分数据，使用权重系数a来加权每个特征变量的重要性，可以使用随机梯度（SGD）来确定这些权重。

线性回归的特点：

1. 建模速度快，使用建模线性关系明显且数据量不大的情况。
2. 有非常直观的理解和解释，常用于机器学习的入门
3. 对异常值非常敏感，建模前最好删除异常值

线性回归的代码实现

成本函数（Cost Function）

使用成本函数J来表示预测结果h(x)与实际输出y之间的误差，这里可以使用最简单的“最小均方误差”（Least mean square）来描述：
：
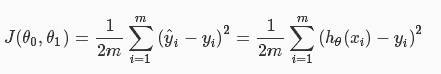
其中，m表示样本的数量，i表示第i个样本，其中的1/2，是为了求导方便而添加的专业习惯。

梯度下降（SGD）

如上文所说，我们需要使用梯度下降确定我们的参数w=和b,使得损失函数J的值最小。
：
关于成本函数J的图像大致像一个“碗”（上），我们来看看J关于一个参数w1（其实应该是theta,代表权重参数）的图像


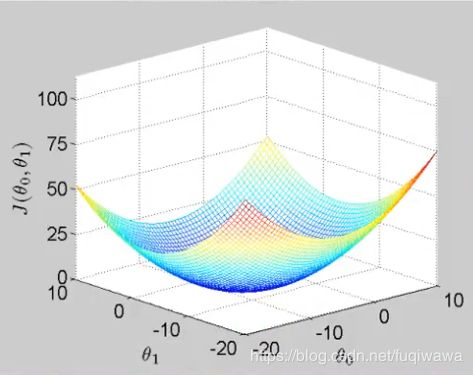
所以按照一般的思路，就是对权重参数求导，使得倒数为0的参数的值，就是成本函数J取得最小值的地方。但是大多时候，求得的偏导的数学表达式很复杂，所以我们采用一种叫做“梯度下降（gradient descent）”的方法

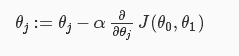
即：

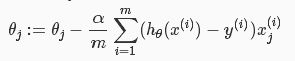
通俗一点讲，就是希望权重参数“沿着J减小的方向（梯度减小的方向），一步一步（也就是学习率alpha）的走到那个最低点”

代码实现——使用sklearn的线性回归模型

class LinearRegression(fit_intercept = True，normalize = False，copy_X = True，n_jobs = 1)
  """
  :param normalize:如果设置为True时，数据进行标准化。请在使用normalize = False的估计器调时用fit之前使用preprocessing.StandardScaler
 
  :param copy_X:boolean，可选，默认为True，如果为True，则X将被复制
 
  :param n_jobs：int，可选，默认1。用于计算的CPU核数
  """

实例代码：

from sklearn.linear_model import LinearRegression
reg = LinearRegression()

波士顿房价预测

1. 波士顿房价的数据描述

from sklearn.datasets import load_boston
boston = load_boston()
print(boston.DESCR)  #查看数据信息

Boston house prices dataset

Data Set Characteristics:

:Number of Instances: 506 

:Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target.

:Attribute Information (in order):

2. 房价数据分割

from sklearn.model_selection import train_test_split

import numpy as np

X = boston.data
y = boston.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=33, test_size=0.25)

3.训练与预测数据标准化处理

from sklearn.preprocessing import StandardScaler

ss_X = StandardScaler()
ss_y = StandardScaler()

X_train = ss_X.fit_transform(X_train)
X_test = ss_X.transform(X_test)
y_train = ss_X.fit_transform(y_train.reshape(-1, 1))
y_test = ss_X.transform(y_test.reshape(-1, 1))

4. 使用线性回归模型对房价进行预测

from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(X_train,y_train)
lr_y_predict = lr.predict(X_test)

5.使用均方误差评测

from sklearn.metrics import mean_squared_error
 
print '线性回归模型的均方误差为：',mean_squared_error(ss_y.inverse_transform(y_test),ss_y.inverse_tranform(lr_y_predict))

完整代码：

from sklearn.linear_model import LinearRegression, SGDRegressor, Ridge
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error



def linearmodel():
    """
    线性回归对波士顿数据集处理
    :return: None
    """

    # 1、加载数据集

    ld = load_boston()

    x_train, x_test, y_train, y_test = train_test_split(ld.data, ld.target, test_size=0.25)

    # 2、标准化处理

    ss_X = StandardScaler()
    ss_y = StandardScaler()

    x_train = ss_X.fit_transform(x_train)
    x_test = ss_X.transform(x_test)
    y_train = ss_y.fit_transform(y_train.reshape(-1, 1))
    y_test = ss_y.transform(y_test.reshape(-1, 1))

    # 3、估计器流程

    # LinearRegression
    lr = LinearRegression()

    lr.fit(x_train, y_train)

    # print(lr.coef_)

    y_lr_predict = lr.predict(x_test)

    y_lr_predict = ss_y.inverse_transform(y_lr_predict)

    print("Lr预测值：", y_lr_predict)

    # SGDRegressor
    sgd = SGDRegressor()

    sgd.fit(x_train, y_train)

    # print(sgd.coef_)

    y_sgd_predict = sgd.predict(x_test)

    y_sgd_predict = ss_y.inverse_transform(y_sgd_predict)

    print("SGD预测值：", y_sgd_predict)

    # 带有正则化的岭回归

    rd = Ridge(alpha=0.01)

    rd.fit(x_train, y_train)

    y_rd_predict = rd.predict(x_test)

    y_rd_predict = ss_y.inverse_transform(y_rd_predict)

    print(rd.coef_)

    # 两种模型评估结果

    print("lr的均方误差为：", mean_squared_error(ss_y.inverse_transform(y_test), y_lr_predict))

    print("SGD的均方误差为：", mean_squared_error(ss_y.inverse_transform(y_test), y_sgd_predict))

    print("Ridge的均方误差为：", mean_squared_error(ss_y.inverse_transform(y_test), y_rd_predict))


print(linearmodel())