2017 LARS:LARGE BATCH TRAINING OF CONVOLUTIONAL NETWORKS (训练大Batch的卷积神经网络)
0. 写在前面
前一段时间调研AI芯片在尽量保证准确率的情况下,如何快速训练大规模数据集并分析其可行性。UC Berkeley的大佬尤洋[1]的这篇
1. 摘要 (Abstract)
加速训练大规模CNN的场景策略是分布式训练(即加多计算节点). 由于data-parallel的SGD的使用和计算节点的增大(成百上千个计算节点),训练的模型精度会剧烈降低。我们认为,目前对大batch的训练策略不够泛化而且可能导致训练无法收敛。
为了克服这个问题,作者提出了一种基于Layer-Wise Aaptive Rate Scaling (LARS) 的学习算法,通过使用LARS, 作者在Alexnet的batch size = 8K,Resnet-50 的batch size = 32K的时候可以让模型收敛而无精度损失。
2. 介绍 (Introduction)
本部分是删节版介绍,一些related work基本不会提及. 如感兴趣, 请查阅英文原版.
我们都知道,训练一个大型的CNN网络是非常耗时的,最直接的加速方式就是增加算力(比如更多的GPU节点),通过data-parallel 的SGD来加速训练。其中, 每个GPU节点(或者AI芯片)接收整体batch (比如8K,32K)中的一部分,为了充分利用计算资源,每个计算节点接收的batch应尽可能大。但是,天下没有免费的午餐,这种通过加计算节点分布式训练的策略,对模型的精度有显著的负面影响。
容易理解,当Epoch保持固定(数据集也不变的时候), 大的batch size意味着权重调整的次数下降/减少. 一个直观的解决方式是(加大)学习率来compensate. 然而,使用更大的学习率会使得网络在初始阶段就发散(这也是为啥近几年warm up策略火的原因)。很多研究人员针对这个问题提出自己的思路,这里不详细介绍,总之:线性调整学习率 + warm up是大batch 训练的state-of-the-art (17年前最好的方法)。
但是,作者使用这种策略来在ImageNet上训练Alexnet,发现batch size在2K后,随着batch size的增大,模型开始出现精度下降甚至发散的情况。为了解决这种情况,作者将Alexnet里面的归一化策略Local Response Normalization (LRN)替换为Batch Normalization (BN),通过将LRN替换为BN,作者发现精度的损失变小了。
为了分析在大学习率下训练的稳定性,作者分析了模型中每层的权值范数和更新的梯度范数。一个有意思的现象被观察到:当这个比例很高时,训练就变得不稳定;当比例很低时,权值的更新变得很慢。因为这个比例在不同层之间差异很大,所以有必要对神经网络中的每一层都使用其独特的学习率。这就是LARS被提出的基础。
与ADAM和RMSProp等学习算法不同的是,LARS:
- 网络中的每层都使用不同的学习率,使得训练更稳定。
- 权值更新的量级与权值的范数有关,这样更好的控制训练的速度。
通过使用LARS,作者声称他们训练的Alexnet-BN和Resnet-50在batch size过万的情况下,精度不出现损失的情况。
3. 背景 (Background)
深度学习中,权值更新(或者说模型学习)的策略如下:
在每一步 t t t时, mini-batch个 x i x_i xi被从训练集中挑选出来,通过计算该mini-batch的损失函数的梯度 ∇ L ( x i , w ) \nabla L(x_i, w) ∇L(xi,w), 网络的权值更新通过随机梯度法如下:
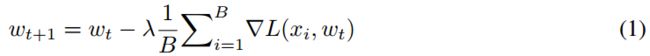
假设我们有 N N N个计算节点,总共的batch size为 B B B, 那么每个计算节点分到的mini-batch为 B N \frac{B}{N} NB个样本。但随着batch加大,我们发现训练就变得愈发困难(模型精度下降乃至发散)。之前的思路为了避免这种问题,会不断的调整一系列超参数(学习率,动量等)。
Krizhevsky[2]指出一种Linear Scaling策略:当我们对 B B B增大 k k k倍时,应该同样对学习率增大 k k k倍(并保持其它超参数不变)。
Linear Scaling背后的逻辑很直接:在保持epoch数量不变的情况下,如果你将batch size加大k倍, 那么更新权重的频次因此降低k倍。所以,加大学习率是一种很自然的方式。
但这种方式对batch size大于2K的情况, 训练变得很难收敛(training diverges), 将Alexnet中的LRN替换为BN后, 效果会好不少~,但是精度还是有损失的。
我们发现,主要的障碍在于高学习率带来的不稳定性,基于此,Goyal[3]等人提出LR+warm up的策略:
training starts with small LR, and then LR is gradually increased to
the target.
这种策略,在 B B B=8K的时候,Resnet-50在无精度损失的情况下收敛,是目前的state-of-the-art。
另一个由大batch带来的问题是:“generalization gap” (泛化差距). Keskar[4]等人指出:large-batch的方法倾向于收敛于训练函数的精确最小化. 但是对泛化性能并没有什么提升…
4. 分析Alexnet在大batch下的训练效果
下表是作者在不同batch size, 不同的基准学习率下,对Alexnet原版和Alexnet-BN版本进行试验的结果统计。
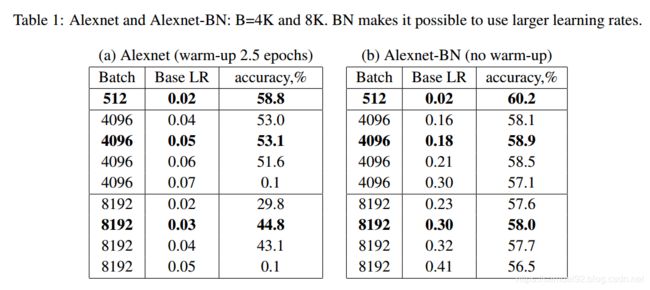
由右表(Alexnet-BN)可以发现, B B B=512和 B B B=8192时,精度掉了2.2个百分点。为了检查这个是不是"generalization gap" . 根据下图的loss图,我们并没有发现 B B B=512和 B B B=8192有显著的差别。

我们的结论是,在这种情况下,精度损失与泛化差距无关,这是由低训练造成的。
5. Layer-wise Adaptive Rate Scaling LARS

首先, 在第一次迭代后,分析每层权值的L2范数和梯度更新的L2范数以及其相应的比值:
∣ ∣ w ∣ ∣ / ∣ ∣ ∇ L ( w t ) ∣ ∣ ||w|| / ||\nabla L(w_t)|| ∣∣w∣∣/∣∣∇L(wt)∣∣.
接着,对每层 l l l使用其独特的学习率 λ l \lambda^{l} λl (Local LR),则其权值更新的值从原来的 Δ w t l = λ ∗ ∇ L ( w t ) \Delta w_{t}^{l} = \lambda * \nabla L(w_t) Δwtl=λ∗∇L(wt)变为 Δ w t l = γ ∗ λ l ∗ ∇ L ( w t l ) \Delta w_{t}^{l} =\gamma *\lambda^{l} *\nabla L(w_t^{l}) Δwtl=γ∗λl∗∇L(wtl). 其中, γ \gamma γ是全局学习率 (global LR),Local LR的定义为:
λ l = η ∗ ∣ ∣ w l ∣ ∣ ∣ ∣ ∇ L ( w l ) ∣ ∣ \lambda^{l} = \eta * \frac {||w^l||} {||\nabla L(w^{l})||} λl=η∗∣∣∇L(wl)∣∣∣∣wl∣∣
η \eta η这个参数决定了一种置信度:即我们有多相信当前层(第 l l l层)会在一次更新中改变它的权重。
需要注意的是,现在,模型中每层权值更新的幅度与梯度的幅度无关,所以这有助于部分消除梯度消失和梯度爆炸等现象。我们的LARS可以扩展到SGD (平衡local LR与weight decay, β \beta β是weight decay系数):
λ l = η × ∣ ∣ w l ∣ ∣ ∣ ∣ ∇ L ( w l ) ∣ ∣ + β ∗ ∣ ∣ w l ∣ ∣ \lambda^{l} = \eta \times \frac {||w^l||} {||\nabla L(w^{l})|| + \beta * ||w^l||} λl=η×∣∣∇L(wl)∣∣+β∗∣∣wl∣∣∣∣wl∣∣
6. 试验结果
训练在Nvidia DGX1上进行,可以看出,试验结果非常不错,比起之前的结果好上不少。
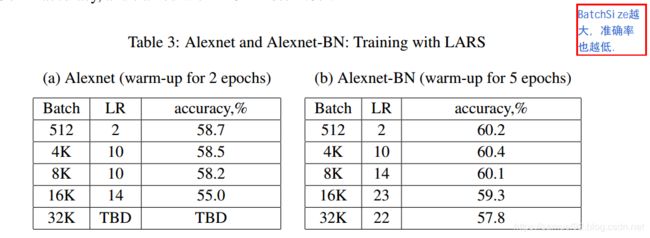
由下图可以看出,带LARS的训练策略, B B B=8K的表现远远比不带LARS的测试集要好。
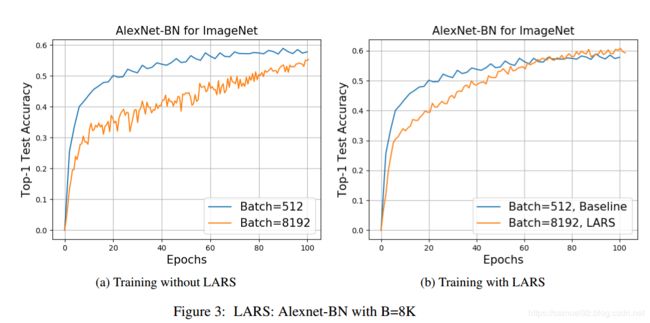
虽然带LARS的SGD比普通SGD的效果更好,但是,也没有达到baseline(即达到 B B B=512的Alexnet的水平)。 但是,这可以通过训练更长的时间来达到。
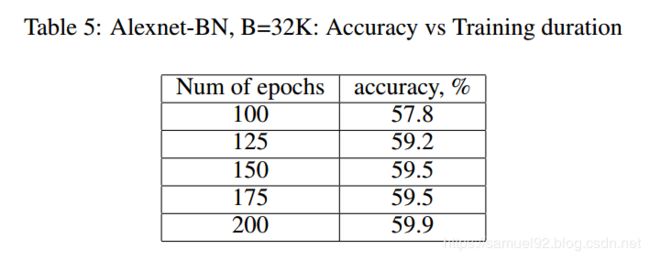
作者认为: 当batch非常大的时候, 随机梯度将与真实梯度非常接近. 所以, bs大的时候相比bs小的时候并没有更多的额外梯度信息. 下表的试验结果验证了这一观点。
7. 结论
大Batch Size是扩大训练卷积网络的核心.
现有的方法通常是采用更大的学习率, 但这不可避免的带来了网络的不收敛. (即便使用warm up策略)
为了解决这个优化问题, 作者提出了LARS, 通过使用LARS, 作者成功的将Resnet50和Alexnet-BN扩展到BS=32k的情况(训练ImageNet).
参考资料
[1]: You Yang, Igor Gitman, Boris Ginsburg:
[2]: Alex Krizhevsky:
[3]: Priya Goyal, Piotr Dollár and et al.
[4]: Nitish Shirish Keskar, Dheevatsa Mudigere, and et al: