webrtc中的噪声抑制之二：噪声估计QBNE

webrtc中的噪声抑制之二：噪声估计QBNE

前言

上一篇学习研究了频域维纳滤波的基本原理，得出两个信噪比计算是实现精准的噪声抑制的前提，那么本篇继续学习研究噪声估计是如何在WebRtc实现的，以及据此而得出的先验信噪比和后验信噪比。

噪声估计

噪声估计是决定噪声抑制的关键，即是难点也是热点，从上文推算过程，webrtc按照STSA（Short-Time-Spectral-Amplitude 短时谱估计）的方法进行噪声估计。我们需要学习和研究的是webrtc采用的那一种最优准侧来实现的维纳滤波自适应过程。关于噪声估计的内容讲解，推荐一篇《语音增强原理之噪声估计》博文，写的深入浅出，这里不再赘述。而翻阅了一些文章，发现用到最多的准则依旧是MMSE（Minimum Mean-Square Error）。WebRtc里是不是也利用了这个准则呢？具体是如何实现的呢？从代码来看，webrtc中包含了两种噪声估计方法，一种是QBNE（Quantile Based Noise Estimation），翻译中文可以叫做分位数噪声估计，前50帧的初始噪声估计是以分位数噪声估计为基础。噪声估计受分位数参数控制，该参数以q表示。根据初始噪声估计步骤确定的噪声估计，仅能用作促进噪声更新/估计的后续流程的初始条件。这个只用在初始噪声估计？另一种也是采用递归的噪声最小估计方法。

QUANTILE BASED NOISE ESTIMATION

分位数噪声估计QBNE是Volker Stahl在他的论文《QUANTILE BASED NOISE ESTIMATION FOR SPECTRAL SUBTRACTION AND WIENER FILTERING》提出来的。朴素的噪声估计方法是逐帧进行语音和非语音分类，具体做法是假设加性噪声影响的语音信号频谱特征仍然保持加性的特点，对于广义稳态的情况，定义如下：
$$x(n)=s(n)+n(n)$$
经过Fourier 傅氏变换到频域
$$X(\omega ,t)=S(\omega ,t)+N(\omega ,t)$$
Fourier 系数表达引入t，标识为在第t帧的数据。在信噪比比较好的环境下，我们定义一个信噪比的门限$\alpha$，如果含噪语音的信噪比大于$\alpha$，这帧被判定为语音，否则判定为噪声，就此得出如下，噪声估计的公式：
$$N(\omega ,t)=\{\begin{array}{ll}N(\omega ,t-1)& \text{if XNR(t) > α}\\ (1-\beta )N(\omega ,t-1)+\beta X(\omega ,t),& \text{else}\end{array}$$
$\beta$是衰减因子，决定噪声估计的自适应速度，信噪比$XNR(t)$定义为：
$$XNR(t)=\frac{{\sum }_{\omega }X(\omega ,t)}{{\sum }_{\omega }N(\omega ,t-1)}$$
但是实际中噪声估计的条件比较复杂，单纯判断语音帧方法也只停留在学习和教学领域了。基于分位数的方法其实是对经典算法的延伸，不需要先验信息，从频域的角度进一步细分，获取判决门限，从文中的试验来看，语音识别率有不错的提升。 分位数噪声估计的想法是建立这样一个共识，即使是语音段，输入信号在某些频带分量也可能没有信号能量。那么假设将某个频带上所有语音帧的能量做一个统计，设定一个分位数值，低于分位数值的认为是噪声，高于分位数值的认为是语音，相比于逐帧判断（VAD），这样就进一步细化的噪声统计的粒度，即使语音帧也能提取有效的噪声信息进行平滑。用公式来表征，假设在$\omega$频率的所有时间帧定义为$X(\omega ,t),t=0,....,T$，这样按照升序来排个序，$X(\omega ,t_0)\le X(\omega ,t_1)\le ...\le X(\omega ,t_T)$。分位数（$q$-quantile）噪声定义如下：
$$N(\omega )=X(\omega ,t_{|q^t|})$$
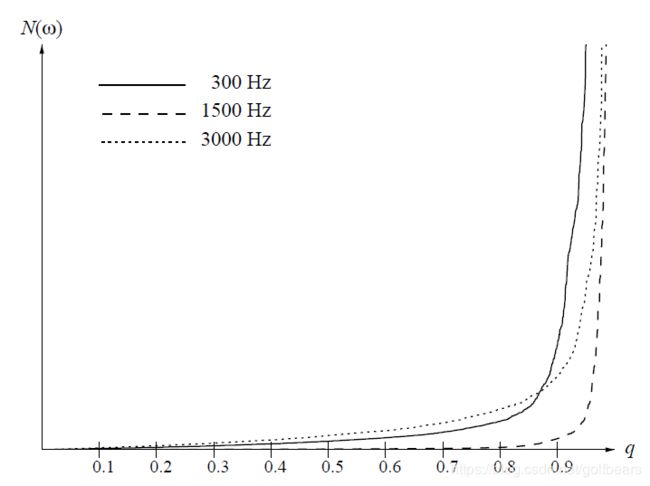
$q$实质表示取所有数据占比分量，但实际应用中往往直接取该分量对应的幅度值，容易引起混淆。$q$=0.5表示统计时间内，能量最低的50%幅度分量的最大值作为噪声门限。引用论文的图来直观的看一下三个频率分量的能量分布图，其中$q$=0.5以为着从0.5的地方划一条竖直线，竖直线和能量的焦点就是该频率的噪声门限。
上述算法从理论上给出噪声估计的可行性研究，但实际使用的时候还需要考虑实时和平滑等问题，不能将所有数据收集好了，排序然后再定$q$值，所以一般会根据先验的工程经验设定初始$q$值，而且还需要动态的作自适应的算法，即所谓的A-QBNE，才能保证该算法在实际应用中可行。
这次我们先看看噪声更新的代码：

static void NoiseEstimation(NoiseSuppressionC* self,
                            float* magn,
                            float* noise) {
  size_t i, s, offset;
  float lmagn[HALF_ANAL_BLOCKL], delta;

  if (self->updates < END_STARTUP_LONG) {
    self->updates++;
  }

  for (i = 0; i < self->magnLen; i++) {
    lmagn[i] = (float)log(magn[i]);
  }

  // Loop over simultaneous estimates.
  for (s = 0; s < SIMULT; s++) {
    offset = s * self->magnLen;

    // newquantest(...)
    for (i = 0; i < self->magnLen; i++) {
      // Compute delta.
      if (self->density[offset + i] > 1.0) {
        delta = FACTOR * 1.f / self->density[offset + i];
      } else {
        delta = FACTOR;
      }

      // Update log quantile estimate.
      if (lmagn[i] > self->lquantile[offset + i]) {
        self->lquantile[offset + i] +=
            QUANTILE * delta / (float)(self->counter[s] + 1);
      } else {
        self->lquantile[offset + i] -=
            (1.f - QUANTILE) * delta / (float)(self->counter[s] + 1);
      }

      // Update density estimate.
      if (fabs(lmagn[i] - self->lquantile[offset + i]) < WIDTH) {
        self->density[offset + i] =
            ((float)self->counter[s] * self->density[offset + i] +
             1.f / (2.f * WIDTH)) /
            (float)(self->counter[s] + 1);
      }
    }  // End loop over magnitude spectrum.

    if (self->counter[s] >= END_STARTUP_LONG) {
      self->counter[s] = 0;
      if (self->updates >= END_STARTUP_LONG) {
        for (i = 0; i < self->magnLen; i++) {
          self->quantile[i] = (float)exp(self->lquantile[offset + i]);
        }
      }
    }

    self->counter[s]++;
  }  // End loop over simultaneous estimates.

  // Sequentially update the noise during startup.
  if (self->updates < END_STARTUP_LONG) {
    // Use the last "s" to get noise during startup that differ from zero.
    for (i = 0; i < self->magnLen; i++) {
      self->quantile[i] = (float)exp(self->lquantile[offset + i]);
    }
  }

  for (i = 0; i < self->magnLen; i++) {
    noise[i] = self->quantile[i];
  }
}

该函数输入的magn是当前帧经过STFT频率矢量幅值，输出的noise是经过估计后的噪声，而历史噪声相关的数据存储在self->density[SIMULT * HALF_ANAL_BLOCKL]，self->lquantile[SIMULT * HALF_ANAL_BLOCKL]，self->quantile[HALF_ANAL_BLOCKL]，self->counter[SIMULT]几个数组中。通过动态tracking的算法，更新self->quantile[HALF_ANAL_BLOCKL]，即噪声的值。“庖丁解牛”吹大了，这个自适应的跟踪算法没有完全分析出来，看来只能以后机缘巧合把它解开了。欢迎各位大神赐教，一解所惑。